- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 小数について(その3)-非循環小数を巡る話題-
コラム
2023年03月01日
文字サイズ
- 小
- 中
- 大
はじめに
非循環小数とは
このシリーズの第1回目の研究員の眼で説明したように、小数には、有限桁の数字で表現される「有限小数」と有限桁の数字では表現できない「無限小数」がある。さらに、無限小数は、同じ数字列が無限に繰り返される「循環小数」とそれ以外の「非循環小数」に区分され、前者は「有理数」、となり、後者は「無理数」になる。
即ち、「非循環小数」は、いわゆる「無理数」と呼ばれているものと同義になる1。これには、以前の研究員の眼で紹介した、円周率πやネイピア数e、さらには平方数ではない自然数nの平方根√n、黄金比φ(=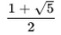 =1.618…)、白銀比τ(=
=1.618…)、白銀比τ(=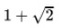 =2.414…)というようなものが含まれることになる。これら以外にも、数学の世界では、多くの「数学定数」と呼ばれるものがあるが、その殆どが無理数となっている。
=2.414…)というようなものが含まれることになる。これら以外にも、数学の世界では、多くの「数学定数」と呼ばれるものがあるが、その殆どが無理数となっている。
さて、これらは非循環小数であるがゆえに、その値の最初の数桁でも覚えるのは容易ではないことになる。そのため、以前の研究員の眼でも紹介したように、その覚え方として、例えば以下のような語呂合わせが存在している。
√2≒1.41421356 (一夜一夜に人見頃)
√3≒1.7320508 (人並みにおごれや)
√5≒2.2360679. (富士山麓オウム鳴く)
√6≒2.44949 (似よよくよく)
√7≒2.64575 (菜に虫いない)
√8≒2.8287271 (にやにや世に無い)(実は、√8=2√2 なので、これは覚える必要はない)
√10≒3.16227 (み色に鮒)
π≒3.141592653589793238462643383279
(産医師異国に向こう産後厄なく産婦みやしろに虫さんざん闇に鳴く) あるいは
(身一つ世一つ生くに無意味いわくなく身ふみや読む似ろよさんざん闇に泣く」
e ≒2.718281828459o45 (鮒一鉢二鉢一鉢二鉢、しごく惜しい)
1 「無理数」に関する話題については、以前の3回の研究員の眼で取り上げた。今回は、無理数の「非循環小数」としての側面に焦点を当てて取り上げている。
即ち、「非循環小数」は、いわゆる「無理数」と呼ばれているものと同義になる1。これには、以前の研究員の眼で紹介した、円周率πやネイピア数e、さらには平方数ではない自然数nの平方根√n、黄金比φ(=
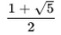 =1.618…)、白銀比τ(=
=1.618…)、白銀比τ(=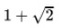 =2.414…)というようなものが含まれることになる。これら以外にも、数学の世界では、多くの「数学定数」と呼ばれるものがあるが、その殆どが無理数となっている。
=2.414…)というようなものが含まれることになる。これら以外にも、数学の世界では、多くの「数学定数」と呼ばれるものがあるが、その殆どが無理数となっている。さて、これらは非循環小数であるがゆえに、その値の最初の数桁でも覚えるのは容易ではないことになる。そのため、以前の研究員の眼でも紹介したように、その覚え方として、例えば以下のような語呂合わせが存在している。
√2≒1.41421356 (一夜一夜に人見頃)
√3≒1.7320508 (人並みにおごれや)
√5≒2.2360679. (富士山麓オウム鳴く)
√6≒2.44949 (似よよくよく)
√7≒2.64575 (菜に虫いない)
√8≒2.8287271 (にやにや世に無い)(実は、√8=2√2 なので、これは覚える必要はない)
√10≒3.16227 (み色に鮒)
π≒3.141592653589793238462643383279
(産医師異国に向こう産後厄なく産婦みやしろに虫さんざん闇に鳴く) あるいは
(身一つ世一つ生くに無意味いわくなく身ふみや読む似ろよさんざん闇に泣く」
e ≒2.718281828459o45 (鮒一鉢二鉢一鉢二鉢、しごく惜しい)
1 「無理数」に関する話題については、以前の3回の研究員の眼で取り上げた。今回は、無理数の「非循環小数」としての側面に焦点を当てて取り上げている。
正規数(正規小数)
さて、非循環小数の中にも、特色のある種類の数が存在している。
「正規数(normal number)」というのは、無限小数表示において数字列が一様に分布しており、数字列が現れる頻度に偏りがないという性質を持つ実数、のことを指している。この概念は、一般的なN進法の場合にも定義されるが、以下では基本的には十進法の場合を考えることとする。
有理数(有限小数や循環小数)は、正規数ではない。有限小数はそもそも無限小数ではないが、仮に、有限桁以降に「0」(あるいは「9」)が循環すると考えたとしても、数字の現れ方は一様にはならないことになる。また、循環小数のうちで、0~9の数字が全て循環する場合(例えば、123456789/9999999999(=13717421/1111111111)= 0.1234567890123456789…)には、0~9までの数字が同じ確率(1/10)で現れてくることになるが、これらは正規数ではない。正規数の定義は、0~9の数字だけでなく、10以上の2桁以上の桁を有する任意の数字列の分布も一様でなければならない。従って、正規数は無理数で非循環小数となる。
なお、「正規(normal)」より弱い概念として「単正規(simply normal)」という概念があるようで、これは十進法の場合、まさに0~9までの数字が同じ確率(1/10)で現れてくる場合を指している(この定義によれば、先の有理数123456789/9999999999(=13717421/1111111111)=0.1234567890123456789… は、「単正規」ということになる)。これに対して、通常の正規は「絶対正規(absolutely normal)」と呼ばれる2。
その定義から、正規数においては、「任意に与えられたn桁の数字列が現れる確率は1/10n」(最初のL桁までに、任意に与えられたn桁の数字列が現れる確率が(Lを無限に大きくしていった時に)1/10nに収束する)ということになる。なお、正規列(正規数の数列)においては、全ての有限数列が現れるが、逆に全ての有限数列が現れる数列が正規であるとは限らない。
正規数の概念は、1909年に、フランスの数学者エミール・ボレル(Émile Borel)(1871-1956)によって導入された。彼は「殆ど全ての」実数が正規数であることを証明した。
また、正規性の定義から明らかなように、正規列に対して、有限個の文字を、加えたり、取り除いたり、変更したり、といった操作を行っても、正規列のままである。従って、正規数の定義において、小数点より前の部分を含めるか否かは本質的ではなく、その意味で「正規小数」という言い方で1未満の数を考えることが多い。
なお、任意の正の数は二つの正規数の積となることが知られているようだ。
非正規数の集合は、非可算無限集合である。例えば、1 を含まない実数は明らかに非正規数であるが、そのような数は非可算無限個存在する。
2 なお、この定義に対して、ある特定の基数に対して「正規」である場合を「単正規(simply normal)」と呼び、2以上の全ての基数に対して「正規」となる場合を「絶対正規(absolutely normal)」と呼ぶこともある。
「正規数(normal number)」というのは、無限小数表示において数字列が一様に分布しており、数字列が現れる頻度に偏りがないという性質を持つ実数、のことを指している。この概念は、一般的なN進法の場合にも定義されるが、以下では基本的には十進法の場合を考えることとする。
有理数(有限小数や循環小数)は、正規数ではない。有限小数はそもそも無限小数ではないが、仮に、有限桁以降に「0」(あるいは「9」)が循環すると考えたとしても、数字の現れ方は一様にはならないことになる。また、循環小数のうちで、0~9の数字が全て循環する場合(例えば、123456789/9999999999(=13717421/1111111111)= 0.1234567890123456789…)には、0~9までの数字が同じ確率(1/10)で現れてくることになるが、これらは正規数ではない。正規数の定義は、0~9の数字だけでなく、10以上の2桁以上の桁を有する任意の数字列の分布も一様でなければならない。従って、正規数は無理数で非循環小数となる。
なお、「正規(normal)」より弱い概念として「単正規(simply normal)」という概念があるようで、これは十進法の場合、まさに0~9までの数字が同じ確率(1/10)で現れてくる場合を指している(この定義によれば、先の有理数123456789/9999999999(=13717421/1111111111)=0.1234567890123456789… は、「単正規」ということになる)。これに対して、通常の正規は「絶対正規(absolutely normal)」と呼ばれる2。
その定義から、正規数においては、「任意に与えられたn桁の数字列が現れる確率は1/10n」(最初のL桁までに、任意に与えられたn桁の数字列が現れる確率が(Lを無限に大きくしていった時に)1/10nに収束する)ということになる。なお、正規列(正規数の数列)においては、全ての有限数列が現れるが、逆に全ての有限数列が現れる数列が正規であるとは限らない。
正規数の概念は、1909年に、フランスの数学者エミール・ボレル(Émile Borel)(1871-1956)によって導入された。彼は「殆ど全ての」実数が正規数であることを証明した。
また、正規性の定義から明らかなように、正規列に対して、有限個の文字を、加えたり、取り除いたり、変更したり、といった操作を行っても、正規列のままである。従って、正規数の定義において、小数点より前の部分を含めるか否かは本質的ではなく、その意味で「正規小数」という言い方で1未満の数を考えることが多い。
なお、任意の正の数は二つの正規数の積となることが知られているようだ。
非正規数の集合は、非可算無限集合である。例えば、1 を含まない実数は明らかに非正規数であるが、そのような数は非可算無限個存在する。
2 なお、この定義に対して、ある特定の基数に対して「正規」である場合を「単正規(simply normal)」と呼び、2以上の全ての基数に対して「正規」となる場合を「絶対正規(absolutely normal)」と呼ぶこともある。
特殊な正規数
特殊な正規数として、例えば以下のものが挙げられる。
ここに、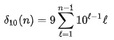 は、n桁の10 進数からの最初の寄与と小数点の間の桁数
は、n桁の10 進数からの最初の寄与と小数点の間の桁数
このチャンパーノウン定数は超越数3でもある。
なお、チャンパーノウン定数は基数 10 に関して正規であるが、他の基数に関して正規であるか否かはわかっていない。
このチャンパーノウン定数は、その乱数性を利用して、プログラミングにおいて、疑似乱数を発生させる場合に使用されたりしている。
3 「超越数(transcendental number)」というのは、有理数を係数に持ついかなる代数方程式の解とはなりえない数(即ち、どんな有理数 a0,a1,…,an を係数とする n 次の代数方程式 a0xn+a1xn-1+…+an-1x+an=0 の解にもならないような数)のことである。複素数(実数を含む)の中で,超越数でないものは「代数的数(algebraic number)」と呼ばれる。
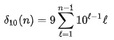 は、n桁の10 進数からの最初の寄与と小数点の間の桁数
は、n桁の10 進数からの最初の寄与と小数点の間の桁数このチャンパーノウン定数は超越数3でもある。
なお、チャンパーノウン定数は基数 10 に関して正規であるが、他の基数に関して正規であるか否かはわかっていない。
このチャンパーノウン定数は、その乱数性を利用して、プログラミングにおいて、疑似乱数を発生させる場合に使用されたりしている。
3 「超越数(transcendental number)」というのは、有理数を係数に持ついかなる代数方程式の解とはなりえない数(即ち、どんな有理数 a0,a1,…,an を係数とする n 次の代数方程式 a0xn+a1xn-1+…+an-1x+an=0 の解にもならないような数)のことである。複素数(実数を含む)の中で,超越数でないものは「代数的数(algebraic number)」と呼ばれる。
このコープランド-エルデシュ定数は無理数である。
チャイティンの定数(Chaitin's constant)
チャイティンの定数は、コンピューターサイエンスの一分野であるアルゴリズム情報理論の概念で、非公式的な言い方では、ランダムに構築されたプログラムが停止する確率を表した実数で、「停止確率(Halting probability)」とも呼ばれている。
アルゼンチン出身で米国在住の数学者グレゴリー・チャイティン(Gregory J. Chaitin)(1947-)の研究から生まれている。
停止確率は、プログラムをエンコードする方法毎に1つずつ、無限に存在している。それぞれの停止確率は正規数かつ超越数であるが、計算不可能で、これらの数字を計算したり、これらの数字を確実に推測したりすることのできるアルゴリズムは存在しない、とされている。
チャイティンの定数は、コンピューターサイエンスの一分野であるアルゴリズム情報理論の概念で、非公式的な言い方では、ランダムに構築されたプログラムが停止する確率を表した実数で、「停止確率(Halting probability)」とも呼ばれている。
アルゼンチン出身で米国在住の数学者グレゴリー・チャイティン(Gregory J. Chaitin)(1947-)の研究から生まれている。
停止確率は、プログラムをエンコードする方法毎に1つずつ、無限に存在している。それぞれの停止確率は正規数かつ超越数であるが、計算不可能で、これらの数字を計算したり、これらの数字を確実に推測したりすることのできるアルゴリズムは存在しない、とされている。
その他の正規数
さて、殆ど全ての実数が正規数であることが知られていると述べた。ただし、その証明は「構成的(constructive)」4でないため、正規数であることが判明している具体的な数は非常に限られている。
一般的に、正規数の例として人工的に作られたものではない数、の正規性を示すことは難しく、例えば、√2、円周率π、ネイピア数e といった有名な数学定数でさえ、正規数であるか否かはわかっていない。
デビッド・H・ベイリー(David H. Bailey )(1948- )と リチャード・クランドール(Richard E. Crandall)(1947-2012)は、2001年に「無理数かつ代数的数である数は正規数である」と予想しているが、これも解決されていないようだ。
4 「構成的証明」とは、対象を作成するか、対象を作成する方法を提供することによって、数学的対象の存在を実証する証明方法をいう。数学の哲学における「構成主義(constructivism)」の「ある数学的対象が存在することを証明するためには、それを実際に見つけたり構成したりしなければならない」という考えに対応している。これは、例を提供せずに特定の種類の対象の存在を証明する「非構成的証明(存在証明又は純粋存在定理とも呼ばれる)」 と対照的なものである。
一般的に、正規数の例として人工的に作られたものではない数、の正規性を示すことは難しく、例えば、√2、円周率π、ネイピア数e といった有名な数学定数でさえ、正規数であるか否かはわかっていない。
デビッド・H・ベイリー(David H. Bailey )(1948- )と リチャード・クランドール(Richard E. Crandall)(1947-2012)は、2001年に「無理数かつ代数的数である数は正規数である」と予想しているが、これも解決されていないようだ。
4 「構成的証明」とは、対象を作成するか、対象を作成する方法を提供することによって、数学的対象の存在を実証する証明方法をいう。数学の哲学における「構成主義(constructivism)」の「ある数学的対象が存在することを証明するためには、それを実際に見つけたり構成したりしなければならない」という考えに対応している。これは、例を提供せずに特定の種類の対象の存在を証明する「非構成的証明(存在証明又は純粋存在定理とも呼ばれる)」 と対照的なものである。
(2023年03月01日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
| 2025/09/25 | 数字の「49」に関わる各種の話題-49という数字に皆さんはどんなイメージを有しているのだろう- | 中村 亮一 | 研究員の眼 |
新着記事
-
2025年10月16日
EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- -
2025年10月16日
再び不安定化し始めた米中摩擦-経緯の振り返りと今後想定されるシナリオ -
2025年10月15日
インド消費者物価(25年10月)~9月のCPI上昇率は1.5%に低下、8年ぶりの低水準に -
2025年10月15日
「生活の質」と住宅価格の関係~教育サービス・治安・医療サービスが新築マンション価格に及ぼす影響~ -
2025年10月15日
IMF世界経済見通し-世界成長率見通しは3.2%まで上方修正
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【小数について(その3)-非循環小数を巡る話題-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
小数について(その3)-非循環小数を巡る話題-のレポート Topへ




















 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




