- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 小数について(その2)-循環小数を巡る話題-
コラム
2023年01月30日
文字サイズ
- 小
- 中
- 大
はじめに
小数という概念は、今からすれば、極めて便利なものとなっているが、分数の考え方が古代エジプトの時代から使用されていたのに比べて、小数点の概念を明示的に含む形で小数が使用されるようになったのは、近代になってからであり、現在のような形に定着したのはそんなに古い話ではない。
小数を巡る話題について、4回に分けて報告することにしているが、前回は、小数の起源や記法等について述べた。今回は、「循環小数」を巡る話題について、述べる。
小数を巡る話題について、4回に分けて報告することにしているが、前回は、小数の起源や記法等について述べた。今回は、「循環小数」を巡る話題について、述べる。
循環小数とは
前回の研究員の眼で説明したように、小数には、有限桁の数字で表現される「有限小数」と有限桁の数字では表現できない「無限小数」がある。さらに、無限小数は、同じ数字列が無限に繰り返される「循環小数」とそれ以外の「非循環小数」に区分され、前者は「有理数」となり、後者は「無理数」になる。
循環節
「循環小数」は、小数点以下のある桁から先で同じ数字の列が無限に繰り返される小数であるが、繰り返される数字の列を「循環節」という。循環小数は有理数として「n/m」(mとnは互いに素)といった形の分数で表される。
ある循環小数の循環節が小数第一位から始まる場合、それを「純循環小数」といい、循環節が小数第二位以降から始まる場合、それを「混合循環小数(あるいは混循環小数)」という。混合循環小数は循環していない有限小数部分とそれ以降の循環している小数部分の二つに分離して考えることができる。
混合循環小数の例として、「1/15(=0.0666666・・・)」や「7/44(=0.15909909・・・)」が挙げられるが、非循環部分は、前者が一桁であるのに対して、後者は二桁となっている。
なお、循環小数の表記として、上記で示したように、循環節となる数字を並べて、最後に「・・・」を付けることに加えて、循環節の両端の数字の上に点(ドット)を付ける場合もある。例えば、以下の通りである。
ある循環小数の循環節が小数第一位から始まる場合、それを「純循環小数」といい、循環節が小数第二位以降から始まる場合、それを「混合循環小数(あるいは混循環小数)」という。混合循環小数は循環していない有限小数部分とそれ以降の循環している小数部分の二つに分離して考えることができる。
混合循環小数の例として、「1/15(=0.0666666・・・)」や「7/44(=0.15909909・・・)」が挙げられるが、非循環部分は、前者が一桁であるのに対して、後者は二桁となっている。
なお、循環小数の表記として、上記で示したように、循環節となる数字を並べて、最後に「・・・」を付けることに加えて、循環節の両端の数字の上に点(ドット)を付ける場合もある。例えば、以下の通りである。
分数表現と小数表現との関係
「n/m」(mとnは互いに素)といった形での分数での表現とこの数字の小数での表現との関係については、mの素因数によって、分数表現が、有限小数になるのか、純循環小数になるのか、混合循環小数になるのか、が決定される。
具体的には以下の通りである(証明は難しくないが、ここでは示していないので、興味のある方は各自で参考資料等をご覧いただきたい)。
即ち、我々が通常使用している十進法の世界において考えると、mが2や5のみを素因数として有している場合には「有限小数」1になるが、mが2や5で割り切れない場合(即ち、10と分母のpが互いに素な場合)には「純循環小数」となり、それ以外の場合(即ち、mが2又は5とそれ以外の素因数の両方を有している場合)には「混合循環小数」となる(なお、こちらが、それぞれの小数の定義という言い方もできるのかもしれないが、分かりやすさの観点から、先の説明をしている)。
1 「有限小数」も、末尾の桁の後ろに 0 が無限に並ぶと見なせば、形式的に循環小数と見なせるし、同様に、0.999... などの数列を用いて、有限小数を循環小数に書き換えることもできることになる。
具体的には以下の通りである(証明は難しくないが、ここでは示していないので、興味のある方は各自で参考資料等をご覧いただきたい)。
1.素因数が2と5のみの場合、有限小数となる。
この時、m=2a・5b と表されるならば、小数以下の有限桁数はaとbの大きい数となる。
2.素因数が2と5以外のみの場合、純循環小数になる。
3.素因数が2又は5、及び2と5以外のものを含む場合、混合循環小数になる。
この時、m=2a・5b ・p(pは2と5を素因数として含まない自然数)と表されるならば、小数以下の循環しない有限桁数はaとbの大きい数となる。
即ち、我々が通常使用している十進法の世界において考えると、mが2や5のみを素因数として有している場合には「有限小数」1になるが、mが2や5で割り切れない場合(即ち、10と分母のpが互いに素な場合)には「純循環小数」となり、それ以外の場合(即ち、mが2又は5とそれ以外の素因数の両方を有している場合)には「混合循環小数」となる(なお、こちらが、それぞれの小数の定義という言い方もできるのかもしれないが、分かりやすさの観点から、先の説明をしている)。
1 「有限小数」も、末尾の桁の後ろに 0 が無限に並ぶと見なせば、形式的に循環小数と見なせるし、同様に、0.999... などの数列を用いて、有限小数を循環小数に書き換えることもできることになる。
循環節の長さ
さて、我々が最も馴染み深い循環小数としては、「1/3(=0.33333・・・)」、「1/7(=0.142857・・・)」「1/11(=0.09090…)」が挙げられるだろう。これでわかるように「循環節」の長さは、「1/3」の場合は1、「1/7」の場合は6、「1/11」の場合には2、となっていて、それぞれ異なっている。
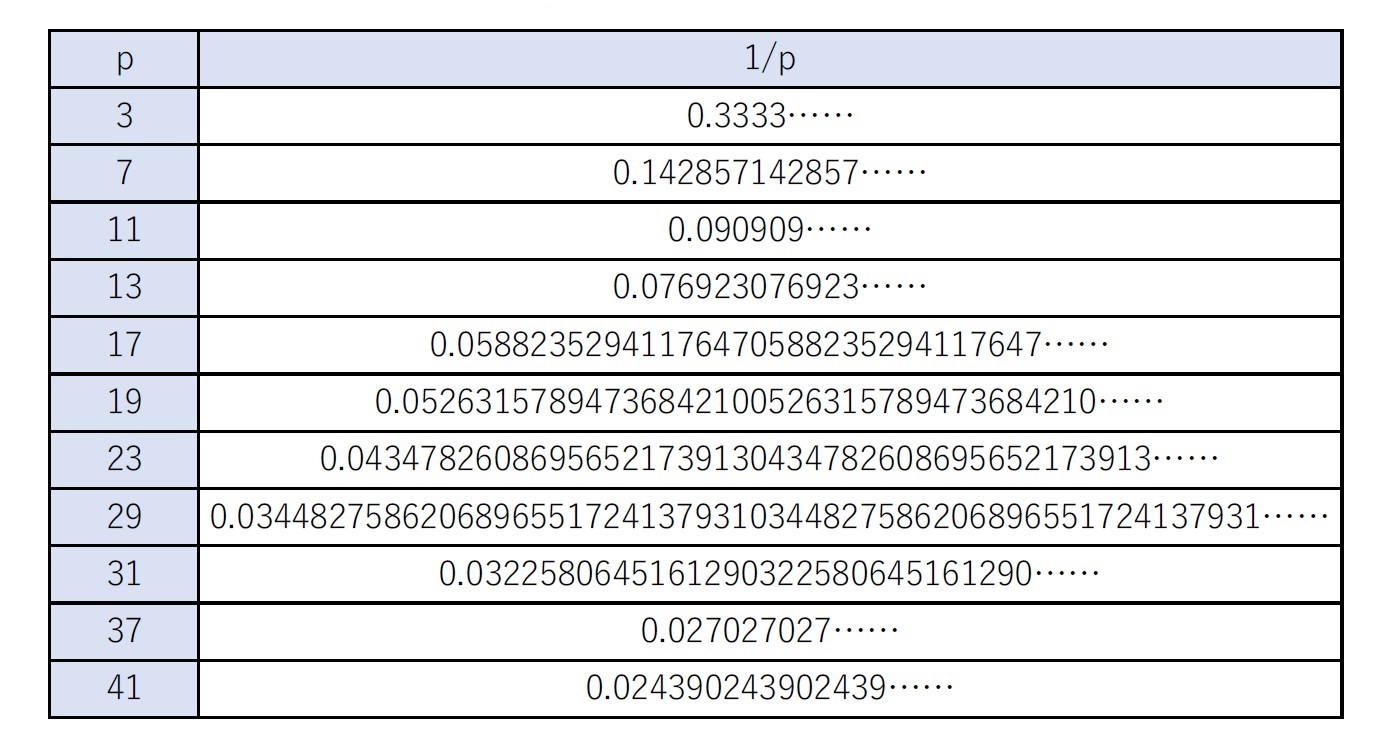
実際に2と5以外の素数pに対する1/pの値と循環節とその長さを調べてみると、例えば以下の図表の通りとなっている。
これを見て、おそらく多くの方々は少し驚かれるのではないかと思われる。「1/29」という数字は確かに循環小数になるのだが、それは何と「28桁の循環節」を有している。「1/7」の6ケタの循環節ですら、結構長いなと感じられる方もいらっしゃると思われる中での「28桁」である。
ところが、こんなところで驚いてはいられない。もっと大きな素数pに対する「1/p」で、その循環節がさらに長いものが存在している。例えば100以下の素数でみても、97に対する「1/97」は何と「96桁の循環節」を有している。
実際に2と5以外の素数pに対する1/pの値と循環節とその長さを調べてみると、例えば以下の図表の通りとなっている。
これを見て、おそらく多くの方々は少し驚かれるのではないかと思われる。「1/29」という数字は確かに循環小数になるのだが、それは何と「28桁の循環節」を有している。「1/7」の6ケタの循環節ですら、結構長いなと感じられる方もいらっしゃると思われる中での「28桁」である。
ところが、こんなところで驚いてはいられない。もっと大きな素数pに対する「1/p」で、その循環節がさらに長いものが存在している。例えば100以下の素数でみても、97に対する「1/97」は何と「96桁の循環節」を有している。
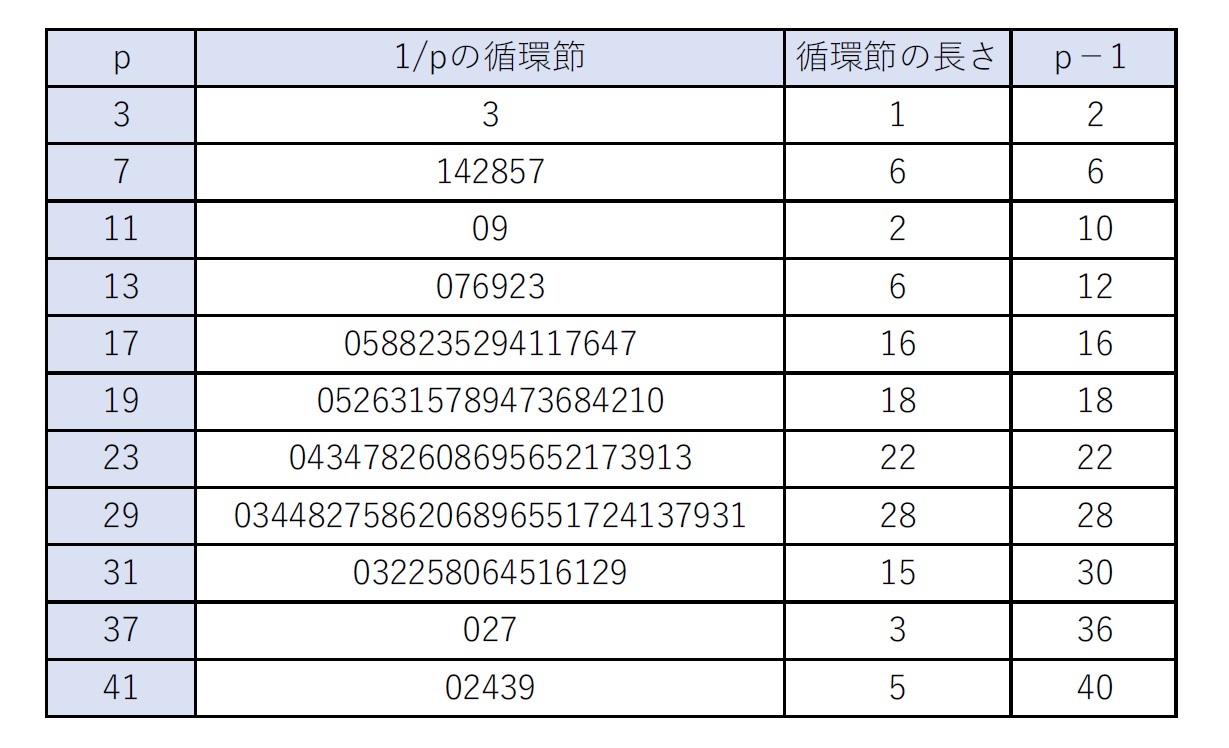
この図表からも一定推測できるかもしれないが、実は循環節の長さに関しては、以下のことが成り立っている。
この研究員の眼では、この証明の説明は行わないので、興味・関心のある方は、専門書等を参照していただければと思っている。
なお、循環節の長さが最大(p-1)であることは、小数の各桁の数値を算出するために、pによる割り算を繰り返していく時に、現れる数値が最大(p-1)個しかないことから明らかである2。
さらには、「1/pの循環節の長さLは、10L-1がpで割り切れる最小の数」(10L≡1(mod p)を満たす最小のL)となる。なぜならば、10L-1がpで割り切れれば、L桁目の割り算の余りが1(より一般的に、a/p(aは自然数)の場合はa)となることから、以後は同じ計算が繰り返される形になるからである。
また、以下で説明する「アルティン予想」が示しているように、逆数1/pの循環節の長さが(p – 1)となる素数pが無限個存在しており、よって、循環節の長さも無限に大きなものが存在すること、が予想されている。
2 「鳩の巣原理(Pigeonhole principle)」又は「引き出し原理(drawer principle)」と呼ばれているものに基づいている。
「2と5以外の素数pの逆数1/pの循環節の長さは、(p – 1)の約数である。」
この研究員の眼では、この証明の説明は行わないので、興味・関心のある方は、専門書等を参照していただければと思っている。
なお、循環節の長さが最大(p-1)であることは、小数の各桁の数値を算出するために、pによる割り算を繰り返していく時に、現れる数値が最大(p-1)個しかないことから明らかである2。
さらには、「1/pの循環節の長さLは、10L-1がpで割り切れる最小の数」(10L≡1(mod p)を満たす最小のL)となる。なぜならば、10L-1がpで割り切れれば、L桁目の割り算の余りが1(より一般的に、a/p(aは自然数)の場合はa)となることから、以後は同じ計算が繰り返される形になるからである。
また、以下で説明する「アルティン予想」が示しているように、逆数1/pの循環節の長さが(p – 1)となる素数pが無限個存在しており、よって、循環節の長さも無限に大きなものが存在すること、が予想されている。
2 「鳩の巣原理(Pigeonhole principle)」又は「引き出し原理(drawer principle)」と呼ばれているものに基づいている。
循環節のパターンの個数
次に、同じ素数pに対して、分子を変化させた場合に、循環節がどのようになっているのかを見てみる。3と7と11の場合は、以下の通りとなる。
1/3=0.3333333… 2/3=0.6666666…
1/7=0.142857142857… 2/7=0.285714285714… 3/7=0.428571428571…
4/7=0.571428571428… 5/7=0.714285714285… 6/7=0.857142857142…
1/11=0.090909… 2/11=0.181818… 3/11=0.272727… 4/11=0.363636…
5/11=0.454545… 6/11=0.545454… 7/11=0.636363… 8/11=0.727272…
9/11=0.818181… 10/11=0.909090…
これをみて皆様もお気付きのことと思われるが、3の場合には、循環節は「3」が続く場合と「6」が続く場合の2つのパターンがあるのに対して、7の場合には、結局は循環開始の数字は異なっているものの、「142857」という1つのパターンのみとなっている。また、11の場合には「09」、「18」、「27」、「36」、「45」の5つのパターンが見られる。
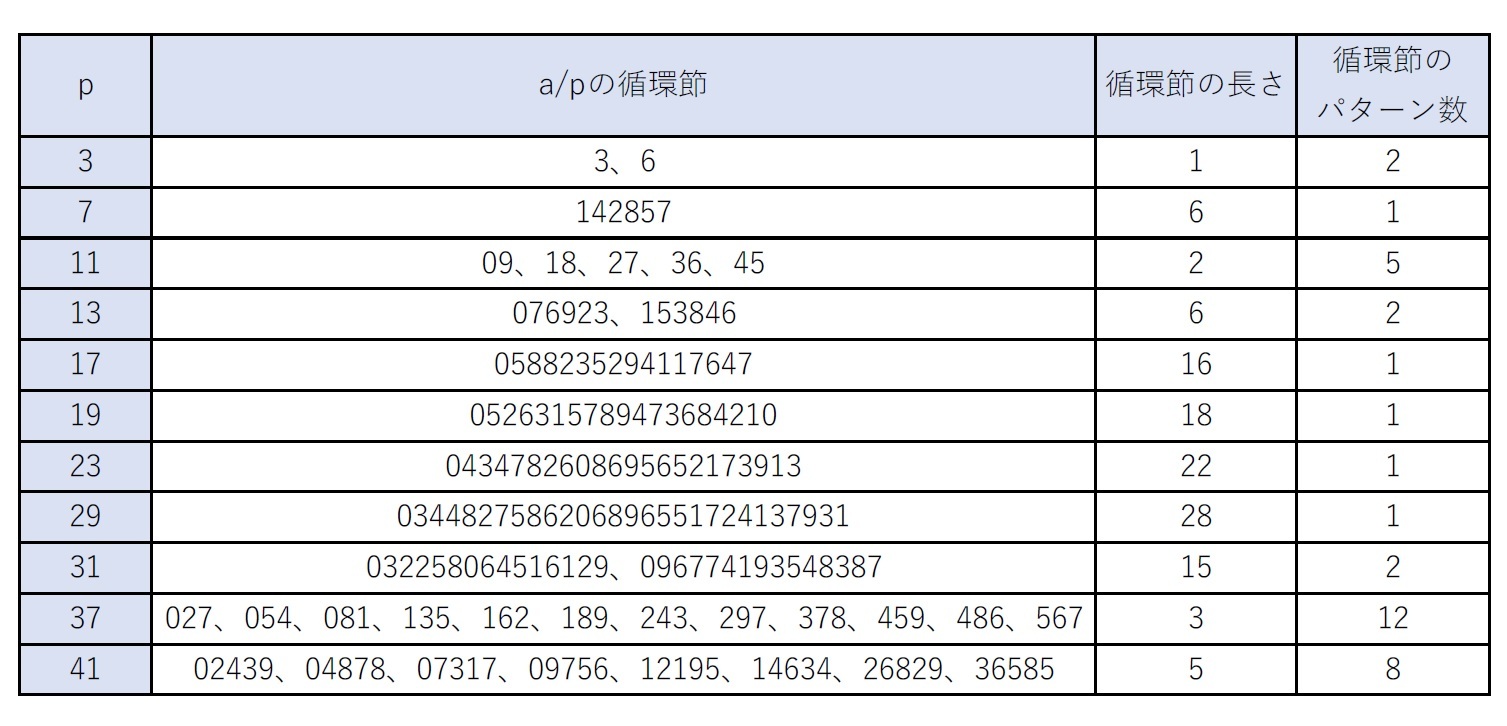
これについても、先ほどの素数pに対するa/p(aは自然数)の値と循環節とそのパターンの個数を調べてみると、以下の図表の通りとなっている。
1/3=0.3333333… 2/3=0.6666666…
1/7=0.142857142857… 2/7=0.285714285714… 3/7=0.428571428571…
4/7=0.571428571428… 5/7=0.714285714285… 6/7=0.857142857142…
1/11=0.090909… 2/11=0.181818… 3/11=0.272727… 4/11=0.363636…
5/11=0.454545… 6/11=0.545454… 7/11=0.636363… 8/11=0.727272…
9/11=0.818181… 10/11=0.909090…
これをみて皆様もお気付きのことと思われるが、3の場合には、循環節は「3」が続く場合と「6」が続く場合の2つのパターンがあるのに対して、7の場合には、結局は循環開始の数字は異なっているものの、「142857」という1つのパターンのみとなっている。また、11の場合には「09」、「18」、「27」、「36」、「45」の5つのパターンが見られる。
これについても、先ほどの素数pに対するa/p(aは自然数)の値と循環節とそのパターンの個数を調べてみると、以下の図表の通りとなっている。
繰り返しになるが、循環節のパターンが1つの場合、循環節の数字を自然数倍しても、各桁に現れる数字の順序は全く同じになる。このような数を「巡回数(Cyclic Number)」あるいは「ダイヤル数」と呼んでいる3。
再び、この図表から推測されるように、「1つの素数に対して、循環節のパターンは複数あっても、その循環説の長さは全て同一」になっている。また、「循環節のパターン数も(p-1)の約数」であり、「『循環節の長さ×循環節のパターン数』は(p-1)」となっている。
なんとも興味深い結果だと思わないだろうか。
3 なお、図表をみてお気付きのように、「142857」以外の巡回数は全て0が先行している。
再び、この図表から推測されるように、「1つの素数に対して、循環節のパターンは複数あっても、その循環説の長さは全て同一」になっている。また、「循環節のパターン数も(p-1)の約数」であり、「『循環節の長さ×循環節のパターン数』は(p-1)」となっている。
なんとも興味深い結果だと思わないだろうか。
3 なお、図表をみてお気付きのように、「142857」以外の巡回数は全て0が先行している。
循環小数の循環節の2分割和
循環節の長さが偶数の場合について、循環節をその真ん中で2つに分割して、その2つを足し算すると、驚くべきことに9が並ぶことになる。
上記の図表で示したケースで見てみると
7 142+857=999
17 05882352+94117647=99999999
29 03448275862068+96551724137931=99999999999999
というような具合である。
小数αの循環節の長さをLとすると、その定義から明らかなように、(10L-1)αは整数となる。
ここで、Lが偶数の場合、(10L-1)=(10L/2-1)(10L/2+1)と分解されることになるが、(10L/2-1)αはLの定義から整数ではないので、(10L/2+1)αが整数ということになる。
実際にα=1/7のケースで見れば、(103+1)×1/7=142.99999999… =143 となっている。
上記の図表で示したケースで見てみると
7 142+857=999
17 05882352+94117647=99999999
29 03448275862068+96551724137931=99999999999999
というような具合である。
小数αの循環節の長さをLとすると、その定義から明らかなように、(10L-1)αは整数となる。
ここで、Lが偶数の場合、(10L-1)=(10L/2-1)(10L/2+1)と分解されることになるが、(10L/2-1)αはLの定義から整数ではないので、(10L/2+1)αが整数ということになる。
実際にα=1/7のケースで見れば、(103+1)×1/7=142.99999999… =143 となっている。
(2023年01月30日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
| 2025/09/25 | 数字の「49」に関わる各種の話題-49という数字に皆さんはどんなイメージを有しているのだろう- | 中村 亮一 | 研究員の眼 |
新着記事
-
2025年10月21日
今週のレポート・コラムまとめ【10/14-10/20発行分】 -
2025年10月20日
中国の不動産関連統計(25年9月)~販売は前年減が続く -
2025年10月20日
ブルーファイナンスの課題-気候変動より低い関心が普及を阻む -
2025年10月20日
家計消費の動向(単身世帯:~2025年8月)-外食抑制と娯楽維持、単身世帯でも「メリハリ消費」の傾向 -
2025年10月20日
縮小を続ける夫婦の年齢差-平均3歳差は「第二次世界大戦直後」という事実
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【小数について(その2)-循環小数を巡る話題-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
小数について(その2)-循環小数を巡る話題-のレポート Topへ




















 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




