- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 分数について(その2)-連分数に関する話題-
コラム
2023年04月18日
文字サイズ
- 小
- 中
- 大
フィボナッチ数と連分数
フィボナッチ数列(Fibonacci sequence)については、以前の研究員の眼「フィボナッチ数列について(その1)-フィボナッチ数列とはどのようなものでどんな性質を有しているのか-」(2021.1.26)等で紹介したが、その最初の数列は、以下の通りとなっている。
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, …
これらの数列に現れてくるフィボナッチ数の隣り合う2つの数の比で表される分数Fn+1/Fnを連分数展開すると、部分商が全て1 となる形で表される。具体的には
5/3=[1;1,1,1]
8/5=[1;,1,1,1,1]
13/8=[1;1,1,1,1,1]
21/13=[1;1,1,1,1,1,1]
というような具合である。
逆に、連分数展開において、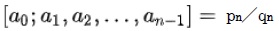 (pnとqnは互いに素な自然数)とするとき、全てのkに対して
(pnとqnは互いに素な自然数)とするとき、全てのkに対して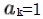 ならば、{pk}はフィボナッチ数列となる。
ならば、{pk}はフィボナッチ数列となる。
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, …
これらの数列に現れてくるフィボナッチ数の隣り合う2つの数の比で表される分数Fn+1/Fnを連分数展開すると、部分商が全て1 となる形で表される。具体的には
5/3=[1;1,1,1]
8/5=[1;,1,1,1,1]
13/8=[1;1,1,1,1,1]
21/13=[1;1,1,1,1,1,1]
というような具合である。
逆に、連分数展開において、
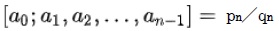 (pnとqnは互いに素な自然数)とするとき、全てのkに対して
(pnとqnは互いに素な自然数)とするとき、全てのkに対して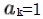 ならば、{pk}はフィボナッチ数列となる。
ならば、{pk}はフィボナッチ数列となる。
連分数の応用
連分数の考え方は、無理数や分母の大きい複雑な有理数を簡単な有理数で近似することに由来している。
連分数は、ディオファントス近似(ある数(実数など)を別のより単純な構造を持つ数(有理数など)で近似する方法)の解を求める手段として有効である。ディオファントス近似は、無理数や超越数の研究と深く関連しており、連分数は無理数の分類や不定方程式(方程式の数よりも未知数の数が多いような方程式)の解法において重要な役割を果たしている。
例えば、今回は紹介できなかったが、代数的数のディオファントス近似の限界に関する「リウヴィルの定理」がある。フランスの数学者かつ物理学者であるジョゼフ・リウヴィル(Joseph Liouville)(1809-1882)は「リウヴィル数」2が超越数であることを証明し、超越数の最初の例を与えた。さらには、以前の研究員の眼「図形数について(その1)-2次元平面図形に関する図形数-」(2022.12.8)で紹介した「ペル方程式」の解法にも利用されている。
なお、連分数は円周率πやネイピア数eが無理数であること(さらには2次の無理数ではないこと)の証明に使用されている。
さらに、べき級数を連分数に変換することで、連分数による解析接続で収束域を拡げることができる。
2 「リウヴィル数」については、研究員の眼「無理数について(その2)-無理数の(有理数や無理数)べき乗や無理数度等-」(2021.12.13)、研究員の眼「小数について(その3)-非循環小数を巡る話題-」(2023.3.1)で紹介した。
連分数は、ディオファントス近似(ある数(実数など)を別のより単純な構造を持つ数(有理数など)で近似する方法)の解を求める手段として有効である。ディオファントス近似は、無理数や超越数の研究と深く関連しており、連分数は無理数の分類や不定方程式(方程式の数よりも未知数の数が多いような方程式)の解法において重要な役割を果たしている。
例えば、今回は紹介できなかったが、代数的数のディオファントス近似の限界に関する「リウヴィルの定理」がある。フランスの数学者かつ物理学者であるジョゼフ・リウヴィル(Joseph Liouville)(1809-1882)は「リウヴィル数」2が超越数であることを証明し、超越数の最初の例を与えた。さらには、以前の研究員の眼「図形数について(その1)-2次元平面図形に関する図形数-」(2022.12.8)で紹介した「ペル方程式」の解法にも利用されている。
なお、連分数は円周率πやネイピア数eが無理数であること(さらには2次の無理数ではないこと)の証明に使用されている。
さらに、べき級数を連分数に変換することで、連分数による解析接続で収束域を拡げることができる。
2 「リウヴィル数」については、研究員の眼「無理数について(その2)-無理数の(有理数や無理数)べき乗や無理数度等-」(2021.12.13)、研究員の眼「小数について(その3)-非循環小数を巡る話題-」(2023.3.1)で紹介した。
連分数の実用的な応用例-暦における閏年の設定-
連分数の実用的な応用例として、暦の策定における閏年の設定がある。
閏年は、太陽年(平均太陽年)の1年365.24218896日(天文年鑑2023による)と365日とのずれを解消するために設定されている。現在使用されている「グレゴリオ暦」では、「西暦が4で割り切れる年を閏年とするが、100で割り切れる年は対象外としつつ、400で割り切れる年は閏年とする」というルールになっており、これにより400年に97回の閏年が設定されることになっている(なお、グレゴリオ暦以前の「ユリウス暦」では「西暦が4で割り切れる年を閏年」としていた)。
ここで、連分数展開によれば、
0.24218896=〔0;4,7,1,3,41,1,1…..〕
となることから、これに基づく近似分数は、順に 1/4、7/29、8/33、31/128・・・ となる。
ここで、
8/33=0.24242424 (0.24218896 との差は0.00023528)
97/400=0.2425 (0.24218896 との差は0.00031104)
であることから、閏年を33年に8回とすれば、現行ルールの400年に97回よりもより太陽年に近いものになる3。
さらに、
31/128=0.2421875 (0.24218896 との差は▲0.00000146)
であることから、「西暦が4で割り切れる年を閏年とするが、128で割り切れる年は対象外とする」というルールにすれば、より太陽年に近いものになる4。
実は、太陽年は少しずつ短くなっている。グレゴリオ暦が議論され始めていた1560年頃の太陽年は約365.2422日であった。これにより、現行のグレゴリオ暦によると、太陽年との差は1年で現行でも約26.8秒程度(さらに太陽年は1年間で約0.05秒短くなっていくので差は拡がっていく)になる。その意味でも、「31/128」に基づくルールの方がより実態に対応したものといえることにもなる。
ただし、簡便性・わかりやすさという観点からは、(現行ルールでも十分に簡便とはいえないかもしれないが)現行ルールに及ばないということなのだろう。
3 ペルシャの天文学者で数学者でもあるウマル・ハイヤーム(1048-1131)が作成した「ジャラーリー暦」がこの方式を採用しており、現在のイラン暦の元となった。
4 現在の「イラン暦」(イランを中心にペルシャ語圏で使われている暦)では、この方式が採用されている。
閏年は、太陽年(平均太陽年)の1年365.24218896日(天文年鑑2023による)と365日とのずれを解消するために設定されている。現在使用されている「グレゴリオ暦」では、「西暦が4で割り切れる年を閏年とするが、100で割り切れる年は対象外としつつ、400で割り切れる年は閏年とする」というルールになっており、これにより400年に97回の閏年が設定されることになっている(なお、グレゴリオ暦以前の「ユリウス暦」では「西暦が4で割り切れる年を閏年」としていた)。
ここで、連分数展開によれば、
0.24218896=〔0;4,7,1,3,41,1,1…..〕
となることから、これに基づく近似分数は、順に 1/4、7/29、8/33、31/128・・・ となる。
ここで、
8/33=0.24242424 (0.24218896 との差は0.00023528)
97/400=0.2425 (0.24218896 との差は0.00031104)
であることから、閏年を33年に8回とすれば、現行ルールの400年に97回よりもより太陽年に近いものになる3。
さらに、
31/128=0.2421875 (0.24218896 との差は▲0.00000146)
であることから、「西暦が4で割り切れる年を閏年とするが、128で割り切れる年は対象外とする」というルールにすれば、より太陽年に近いものになる4。
実は、太陽年は少しずつ短くなっている。グレゴリオ暦が議論され始めていた1560年頃の太陽年は約365.2422日であった。これにより、現行のグレゴリオ暦によると、太陽年との差は1年で現行でも約26.8秒程度(さらに太陽年は1年間で約0.05秒短くなっていくので差は拡がっていく)になる。その意味でも、「31/128」に基づくルールの方がより実態に対応したものといえることにもなる。
ただし、簡便性・わかりやすさという観点からは、(現行ルールでも十分に簡便とはいえないかもしれないが)現行ルールに及ばないということなのだろう。
3 ペルシャの天文学者で数学者でもあるウマル・ハイヤーム(1048-1131)が作成した「ジャラーリー暦」がこの方式を採用しており、現在のイラン暦の元となった。
4 現在の「イラン暦」(イランを中心にペルシャ語圏で使われている暦)では、この方式が採用されている。
最後に
今回は、分数を巡る話題のうち、連分数に関する話題について、述べてきた。
連分数については、恐らく殆どの人が、学生時代に学んだという記憶はなく、その意味で「連分数」という言葉を初めて聞いたという方も多かったものと思われる。ただし、紀元前300年のユークリッドの原論に、最大公約数のアルゴリズムが含まれており、その現代バージョンでは、連続するユークリッド除算の商の列として連分数が生成されている。即ち、ユークリッドの互除法5のアルゴリズムが連分数の計算手順そのものになっている(ユークリッドの互除法については、現在は高校の数学で学ぶようになっているだ)。また、5 世紀のインドの数学者アリャバタ(Aryabhata)による論文アーリャバティヤ(Aryabhatiya)には、連分数を使用した不定方程式の解が含まれている。
このように、連分数という考え方自体は、古い歴史を有しており、連分数は以前から有用な手法として使用されてきたものである。また、現在も数論における研究対象になっている。今回は紹介できなかったが、連分数の周期構造等についてもいくつかの事実が証明されている。また、関数を分子と分母に有する関数項連分散を考えることもできる。
今回の研究員の眼を通じて、少しは連分数に興味・関心を有していただければと思って紹介することにした。
次回は、分数を巡る話題のうち、既約分数に関する話題について、述べることとする。
5 2 つの自然数 a, b (a ≧ b) について、a の b による剰余を r とすると、 a と b との最大公約数は b と r との最大公約数に等しいという性質が成り立つことを利用して、 b を r で割った剰余、 除数 r をその剰余で割った剰余、と剰余を求める計算を逐次繰り返すことで、剰余が 0 になった時の除数が a と b との最大公約数となるというアルゴリズムで、2つの自然数の最大公約数を求める手法
連分数については、恐らく殆どの人が、学生時代に学んだという記憶はなく、その意味で「連分数」という言葉を初めて聞いたという方も多かったものと思われる。ただし、紀元前300年のユークリッドの原論に、最大公約数のアルゴリズムが含まれており、その現代バージョンでは、連続するユークリッド除算の商の列として連分数が生成されている。即ち、ユークリッドの互除法5のアルゴリズムが連分数の計算手順そのものになっている(ユークリッドの互除法については、現在は高校の数学で学ぶようになっているだ)。また、5 世紀のインドの数学者アリャバタ(Aryabhata)による論文アーリャバティヤ(Aryabhatiya)には、連分数を使用した不定方程式の解が含まれている。
このように、連分数という考え方自体は、古い歴史を有しており、連分数は以前から有用な手法として使用されてきたものである。また、現在も数論における研究対象になっている。今回は紹介できなかったが、連分数の周期構造等についてもいくつかの事実が証明されている。また、関数を分子と分母に有する関数項連分散を考えることもできる。
今回の研究員の眼を通じて、少しは連分数に興味・関心を有していただければと思って紹介することにした。
次回は、分数を巡る話題のうち、既約分数に関する話題について、述べることとする。
5 2 つの自然数 a, b (a ≧ b) について、a の b による剰余を r とすると、 a と b との最大公約数は b と r との最大公約数に等しいという性質が成り立つことを利用して、 b を r で割った剰余、 除数 r をその剰余で割った剰余、と剰余を求める計算を逐次繰り返すことで、剰余が 0 になった時の除数が a と b との最大公約数となるというアルゴリズムで、2つの自然数の最大公約数を求める手法
(2023年04月18日「研究員の眼」)
関連レポート
- 分数について(その1)-分数の起源等はどうなっているのか-
- 無理数について(その2)-無理数の(有理数や無理数)べき乗や無理数度等-
- 小数について(その2)-循環小数を巡る話題-
- フィボナッチ数列について(その1)-フィボナッチ数列とはどのようなものでどんな性質を有しているのか-
- 図形数について(その1)-2次元平面図形に関する図形数-
- 小数について(その3)-非循環小数を巡る話題-
- 黄金比φについて(その1)-黄金比とはどのようなものなのか-
- 白銀比τ等について-白銀比とはどのようなもので、どんな場面で使用されているのか-
- ネイピア数eについて-ネイピア数とは何か、ネイピア数はどんな意味を有しているのか-
- 円周率πが現われる世界-ビュフォンの針の問題-
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
新着記事
-
2025年11月04日
今週のレポート・コラムまとめ【10/28-10/31発行分】 -
2025年10月31日
交流を広げるだけでは届かない-関係人口・二地域居住に求められる「心の安全・安心」と今後の道筋 -
2025年10月31日
ECB政策理事会-3会合連続となる全会一致の据え置き決定 -
2025年10月31日
2025年7-9月期の実質GDP~前期比▲0.7%(年率▲2.7%)を予測~ -
2025年10月31日
保険型投資商品の特徴を理解すること(欧州)-欧州保険協会の解説文書
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【分数について(その2)-連分数に関する話題-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
分数について(その2)-連分数に関する話題-のレポート Topへ



















 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




