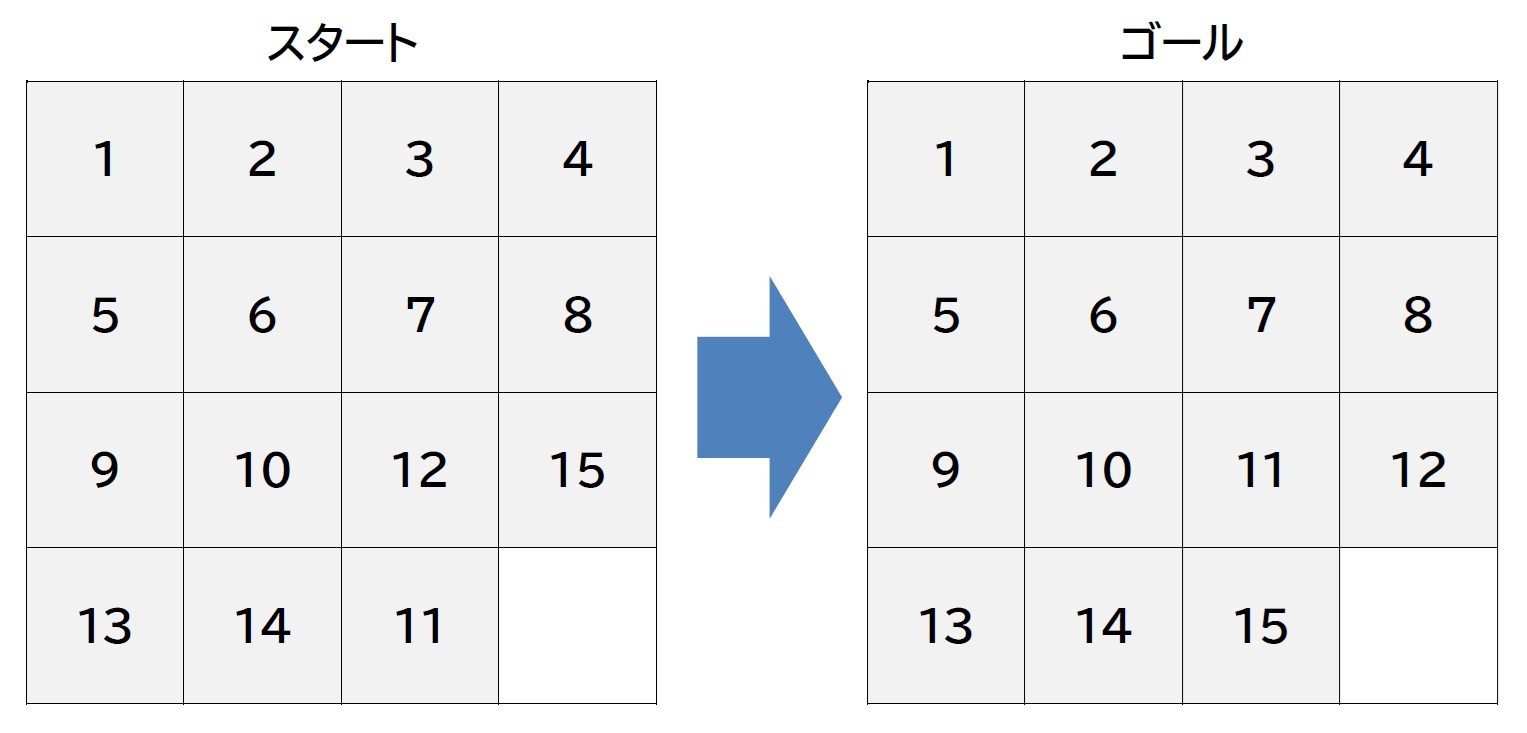
15パズルの確率－ランダムに設定したパズルが解ける確率は?

保険研究部主席研究員兼気候変動リサーチセンターチーフ気候変動アナリスト兼ヘルスケアリサーチセンター主席研究員篠原拓也

このレポートの関連カテゴリ

◇ “予想”が正しいことの確認は、稿末の(参考)に

あとは、“予想”が正しいことを確認していくだけだ。

ただ、なんとなく想像できるように、数学に興味がない方にとっては、この確認は機械的で味気ない感じがしてしまうはずだ。パズルマニアに、「本当は、ここが面白いのだが…」などと言われても、つまらないものはつまらないとしか感じようがないだろう。

よい例えかどうかはわからないが、このことは、「焼き魚で、本当に美味いのは、身ではなくワタ(内臓)の部分だ」と言われても、これに賛同できない人は、どうやっても賛同できないといったことと、どこか似たような話のように思われる。

そこで、“予想”が正しいことの確認については、稿末に(参考)として付けることにする。興味のある方はご覧いただきたい。

◇ パズルが解ける確率を考えてみることも面白いかも

本稿では、15パズルについて、15個のブロックをランダムに置いたときに完成できる確率を考えてみた。

冒頭に挙げたように、世の中にはさまざまな種類のパズルがある。パズルはいろいろ試行錯誤をしながら解くことに醍醐味がある。

それとともに、「このパズルが解ける確率はどれくらいだろうか」といった、パズルの構造について考えてみることも面白いように思われるが、いかがだろうか。

(参考資料)

「群論入門－対称性をはかる数学」芳沢光雄著(講談社, ブルーバックスB-1917, 2015年)

“15 puzzle”(Wikipedia)

(参考)「互換が偶数個の置換は完成できる、奇数個の置換は完成できない」との“予想”の確認

確認には、いくつかのステップを踏む必要がある。数学でいう厳密な証明ではなく、以下は考え方の確認にとどめる。((参考資料)の「群論入門－対称性をはかる数学」芳沢光雄著(講談社, ブルーバックスB-1917, 2015年)の内容を参考としている。)

[ステップ(1)]
まず、ある置換が「ゴール」の状態を完成できる(以下、「完成可能」という)置換であったとき、その逆置換(「ゴール」の状態から「スタート」の状態に戻す置換)も完成可能となる。また、ある置換と別の置換がいずれも完成可能であったとき、その合成置換(複数の置換を続けて行うことでできる置換)も完成可能となる。

逆置換については、「スタート」と「ゴール」の状態を入れ替えたと思えば、完成可能と理解できる。

合成置換については、2つの置換を考えたときに、1つ目の置換を終えた後の「ゴール」の状態を、2つ目の置換を行う前の「スタート」の状態に入れ替えることで、完成可能となるとわかる。

[ステップ(2)]
次に、パズルの3つの場所u1, u2, u3のブロックを、他の3つの場所v1, v2, v3にそれぞれ移す置換で完成可能なものがあることを確認する。ただし、この場合、一番右下の空白部分(「ゴール」の状態の「16」の部分)を除いた、それ以外の場所については、どうなっても構わないとする。

まず、「ゴール」の状態における「1」「2」「3」の場所を1, 2, 3と呼ぶことにする。

そして、(3つの場所u1, u2, u3のブロックを、他の3つの場所v1, v2, v3にそれぞれ移す置換)は、(u1を1に、u2を2に、u3を3に移す置換)と、((v1を1に、v2を2に、v3を3に移す置換)の逆置換)の合成置換として表すことができる。

(u1を1に、u2を2に、u3を3に移す置換) と、(v1を1に、v2を2に、v3を3に移す置換)には、どちらも完成可能なものがあるので、それをとる。そして、ステップ(1)でみた、完成可能な置換の逆置換や合成置換は完成可能であるということを用いて、(3つの場所u1, u2, u3のブロックを、他の3つの場所v1, v2, v3にそれぞれ移す置換)には完成可能なものがあることがわかる。

[ステップ(3)]
続いて、3つのブロックa, b, cを考えたときに、aをbに、bをcに、cをaに移す置換(以下、「巡回置換」という)は完成可能となることを確認する。

これには、まず、「11」,「12」,「15」の3つのブロックからなる巡回置換が完成可能であることを確認する。次の左図で、「15」を下に、「12」を右に、「11」を上に、「15」を左に動かせば、完成可能であることがわかる。

そのうえで、(aを「11」に、bを「12」に、cを「15」に移す置換)を考える。

(a, b, cからなる巡回置換)は、(aを「11」に、bを「12」に、cを「15」に移す置換)と、(「11」,「12」,「15」からなる巡回置換)と、((aを「11」に、bを「12」に、cを「15」に移す置換)の逆置換)の合成置換として、表すことができる。

ステップ(2)で確認した通り、((aを「11」に、bを「12」に、cを「15」に移す置換)には、完成可能なものがある。そこで、そのような完成可能な置換のうちから適当に1つとってきて、これを、「(aを「11」に、bを「12」に、cを「15」に移す完成可能な置換)」と呼ぶことにする。

そうすると、(a, b, cからなる巡回置換)は、(aを「11」に、bを「12」に、cを「15」に移す完成可能な置換)と、(「11」,「12」,「15」からなる巡回置換)と、((aを「11」に、bを「12」に、cを「15」に移す完成可能な置換)の逆置換)の合成置換として、表すことができる。ステップ(1)で確認したことを用いて、(a, b, cからなる巡回置換)は完成可能であることがわかる。

[ステップ(4)]
そして、ついに、すべての偶置換は完成可能であることを示す。偶置換は偶数個の互換の合成置換であるから、(pとqの互換)と(sとtの互換)の、2つの互換の合成置換に着目する。

このとき、合成置換は3つのパターンに分類できる。(i) p, q, s, tがいずれも異なる場合、(ii) pとsは同じだが、qとtは異なる場合、(iii) pとs、qとtがそれぞれ同じ場合の3つだ。

(i)の場合
2つの互換の合成置換は、(q, s, tからなる巡回置換)と、(p, q, sからなる巡回置換)の合成となる。巡回置換の合成なので、ステップ(1)とステップ(3)で確認したことから、完成可能となる。

(ii)の場合
2つの互換の合成置換は、(p, q, tからなる巡回置換)となるので、ステップ(3)で確認したことから、完成可能となる。

(iii)の場合
2つの互換の合成置換は、2回の置換で元に戻るので何も変わらない置換となる。これは、(p, q, z(zは何でもよい)からなる巡回置換)と、(z, q, pからなる巡回置換)の合成と表すことができるので、ステップ(1)とステップ(3)で確認したことから、完成可能となる。

すべての偶置換は、2つの互換の合成置換の合成と表せるため、完成可能となる。

[最後に、奇置換の場合は完成できないことの確認]
完成できない例として挙げたサム・ロイド氏の問題は互換が奇数個(1個)であった。最後に、こうした奇置換の場合は完成できないことを確認しよう。

「スタート」の状態と「ゴール」の状態で、空白部分が同じ位置(右下)にあることに着目する。空白部分が同じ位置にあるためには、偶数回移動する必要がある。つまり、完成するためには、空白部分が偶数回移動することが条件となる。この空白部分を、3ページで述べたように、「16」のブロックと考えることにしよう。

奇置換で完成できるとした場合、「16」のブロックは奇数回動く必要がある。例えば、サム・ロイド氏の問題で、(「14」と「15」の互換)を行うためには、(「14」と「16」の互換)と、(「15」と「16」の互換)と、(「14」と「16」の互換)という、「16」との互換が3個(奇数個)必要となる。「14」と「15」以外のブロックを動かす場合は、それを元の位置に戻す必要があるため、「16」とそのブロックの互換が偶数個必要となる。結局、奇数個と偶数個の足し算となり、「16」との互換の数は奇数個となる。

だが、これは、完成するまでには空白部分である「16」が偶数回移動する必要があるという条件に反する。これは、奇置換の場合は完成できないことを示している。

日付	タイトル	執筆者	媒体
2025/03/25	産業クラスターを通じた脱炭素化－クラスターは温室効果ガス排出削減の潜在力を有している	篠原拓也	基礎研レター
2025/03/18	気候変動:アクチュアリースキルの活用－「プラネタリー・ソルベンシー」の枠組みに根差したリスク管理とは?	篠原拓也	基礎研レター
2025/03/11	国民負担率 24年度45.8%の見込み－高齢化を背景に、欧州諸国との差は徐々に縮小	篠原拓也	研究員の眼
2025/03/04	サイバーリスクのモデリング－相互に接続されたシステミックリスクをどうモデリングする?	篠原拓也	保険・年金フォーカス

日付

タイトル

執筆者

媒体

2025/03/25

産業クラスターを通じた脱炭素化－クラスターは温室効果ガス排出削減の潜在力を有している

篠原拓也

基礎研レター

2025/03/18

気候変動:アクチュアリースキルの活用－「プラネタリー・ソルベンシー」の枠組みに根差したリスク管理とは?

篠原拓也

基礎研レター