エレベータが下向きの確率は?－ガモフ－スターンのエレベーター問題をみてみよう

保険研究部主席研究員兼気候変動リサーチセンターチーフ気候変動アナリスト兼ヘルスケアリサーチセンター主席研究員篠原拓也

このレポートの関連カテゴリ

日常生活のなかでは、確率が気になることがある。天気予報の降水確率や宝くじの当せん確率は、なじみ深いものの1つと言えるだろう。

時には、“この確率はどれくらいなのか?” が、気になることもある。例えば、生まれてくる子どもが女の子である確率、道路を歩いていて交通事故に遭う確率、カプセル自動販売機(通称「ガチャガチャ」)を10回まわすうちに同種のカプセルトイがコンプリートする(全ての種類が揃う)確率、などだ。

そういう気になる確率の1つとして、エレベーターに関するものがある。ある7階建のビルの6階のエレベーターホールで、下の階に降りようとして、エレベーターを待っていたとする。このとき、次に来るエレベーターが下向きである確率はどれくらいか?　といったものだ。

これについては、「ガモフ－スターンのエレベーター問題」という有名な話がある。今回は、この問題について少し考えてみよう。

◇ 問題の発端は研究所内のエレベーターでの移動

この問題を提起したジョージ・ガモフは、旧ロシア帝国領(現在はウクライナ)オデーサ生まれのアメリカの物理学者だ。ビッグバン宇宙論の提唱や、宇宙マイクロ波背景放射の予言など、宇宙進化論の研究で有名だ。

問題を提起したもう1人は、マーヴィン・スターンで、彼もアメリカの物理学者だ。この2人は、サンディエゴの7階建てのビルで研究をしていた。ガモフは2階、スターンは6階に研究室を持っていた。お互いの研究室を訪ねる際にはエレベーターを利用するのだが、エレベーターを待つときに、ある疑問が生じたという。

ガモフがスターンの研究室を訪ねようとして上向きのエレベーターを待っていると、下向きのエレベーターが来ることが多かった。一方、スターンがガモフの研究室を訪ねようとして下向きのエレベーターを待っていると、上向きのエレベーターが来ることが多かった。

この現象をどのように説明すべきか、2人は確率を用いて解き明かそうとした。

◇ エレベーターにはいくつかの仮定が置かれている

この問題を考えるうえで、いくつかの仮定を置く。

・エレベーターの各台は、独立して、一番上の階から一番下の階まで連続的なサイクルで上下に移動するものとする。なお、各階の高さは同じとする。

・エレベーターの各台は、同じ速度で移動し、各階での平均の待ち時間も同一と仮定する。

・ある階でボタンが押されたときに、各台は、それぞれの上下移動のサイクルのランダムな位置にいるものとする。

この問題で取り上げているエレベーターは、「どこかの階で待機していて、ボタンが押されたらその階に向かって移動していく」といったオフィスビルやマンションのエレベーターとは異なる。買い物客で賑わっているときのデパートのエレベーターのように、「エレベーターが常に上下に移動していて、どのエレベーターが来るかは各エレベーターの上下移動のサイクルしだい」という状況だ。まず、その点に注意しておこう。

◇ 7階建のビルの2階で待っている ― 次に来るエレベーターが下向きの確率は5/6

b階建のビルのa階で待っているとしよう。ここで、aは1からbのいずれでもよいのだが、上述のエレベーターの仮定から、「2階で待っていて次に来るエレベーターが下向きの確率」と、「(b-1)階で待っていて次に来るエレベーターが上向きの確率」(＝1－「(b-1)階で待っていて次に来るエレベーターが下向きの確率」)は、同じになることがわかる。つまり、下層階で待っているケースを調べれば、上層階で待っているケースは計算できる。

そこで、下層階で待っている（すなわち a≦(b+1)/2 ）ことにする。例えば、8階建(b=8)の場合は4階以下、9階建(b=9)の場合は5階以下で待っている、ということにする。

エレベーターが1台の場合は、話は簡単だ。エレベーターは、つねに、1階からb階までの(b-1)の高さの空間のどこかにいる。ボタンを押したときに、下向きのエレベーターが来るためには、エレベーターがa階より上にいなくてはならない。

a階より上の空間は(b-a)だから、ボタンを押したときに、エレベーターがa階より上にいる確率は、(b-a)/(b-1)となる。これが、次に来るエレベーターが下向きの確率となる。次に来るエレベーターが上向きの確率は、1－(b-a)/(b-1)＝(a-1)/(b-1) となる。

これからの話で、式を簡単に表示するために、次に来るエレベーターが上向きの確率をpとしておく。p＝(a-1)/(b-1) だ。ここで、a≦(b+1)/2としていたので、p≦1/2となることに注意しておこう。

次に来るエレベーターが下向きの確率は、1からpを引き算して、(1-p) となる。

これは、1/2 ＋ 1/2 × (1-2p) と表すことができる。

7階建のビルで(b=7)、2階にいるガモフが(a=2)、スターンの研究室を訪ねようとしてエレベーターを待っているケースでは、次に来るエレベーターが下向きの確率は5/6(=(7-2)/(7-1))、上向きの確率は1/6(=(2-1)/(7-1))となる。たしかに、下向きのエレベーターが来ることが多いことが確認できる。

◇ エレベーターの台数が2台だと、次に来るエレベーターが下向きの確率は…

この問題が難しくなるのは、エレベーターの台数が複数の場合だ。まず、台数が2台の場合を考えよう。2台のエレベーターに、1)、2)の番号をつけておく。

a階に次に来るエレベーターは1)かもしれないし、2)かもしれない。次に来るエレベーターが下向きであるケースを、2つに場合分けしてみる。

(1) 1)と2)のどちらもa階より上の空間にいて、どちらかが次に来るケース

(2) 1)と2)のうち、片方がa階より上の空間、もう片方がa階より下の空間にいて、両者が競争をした結果、a階より上の空間にいたエレベーターが先に来るケース

1)と2)のどちらもa階より下の空間にいる場合は、次に来るエレベーターは上向きとなるので、考えなくてよい。

まず、(1)の確率。これは、(1-p)²となる。

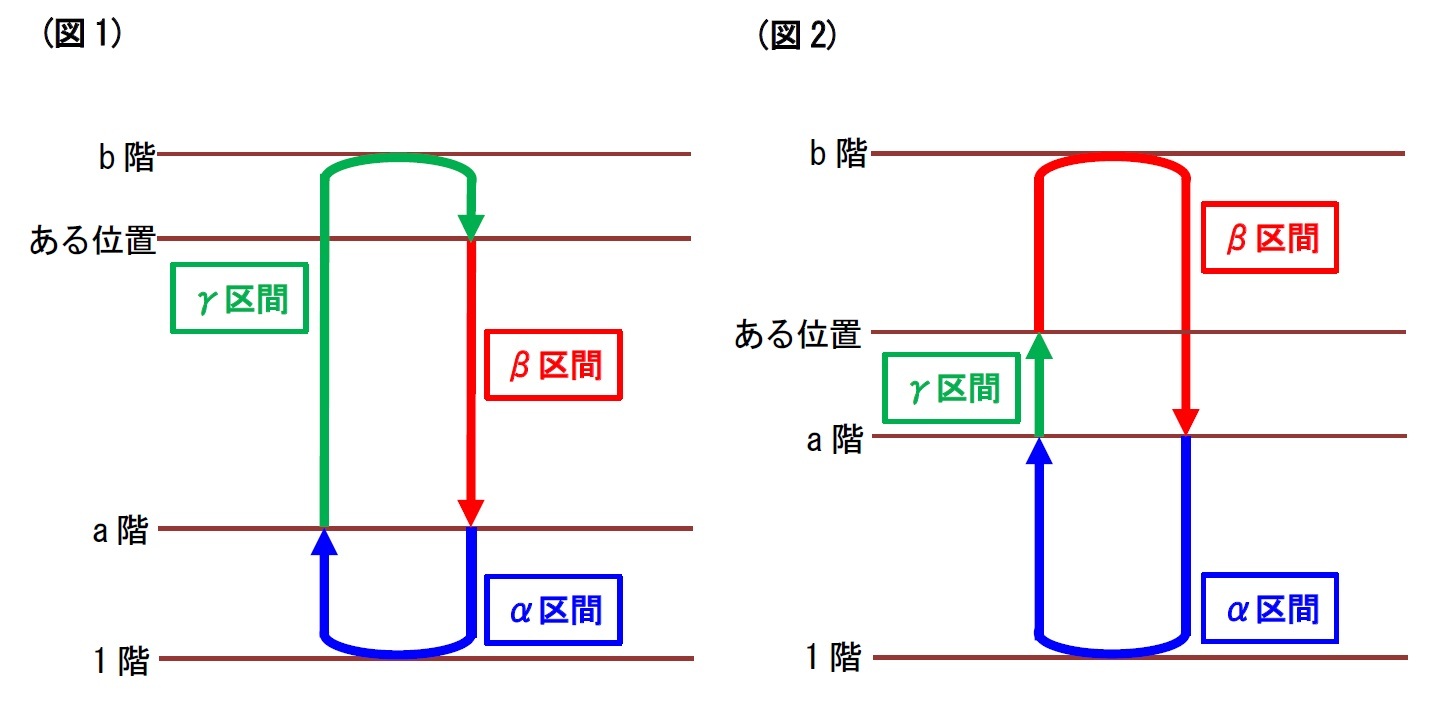
次に、(2)の確率。これは、少しややこしい。a階より上の空間にいるエレベーターが、a階より下の空間にいるエレベーターより先にa階に来るためには、a階より上の空間にいるエレベーターは、「“a階から1階に下がり、またa階に上がってくるのと同じ時間をかけて、a階に下がってくるa階より上の空間のある位置”からa階まで」の間にいる必要がある。この「」内、特に“ ”内のある位置は、文を読んだだけでは何を言っているのかわかりづらい。次の図で見ていくことにしよう。

a階から1階に下がり、またa階に上がってくるのと同じ時間をかけて、a階に下がってくるa階より上の空間のある位置

1台のエレベーターの上下移動のサイクルを図示したのが上図だ。実際は単なる上下移動をするが、サイクルであることをわかりやすくするために、図では時計回りの周回移動として表示している。

青色部分は、a階から1階に下がり、またa階に上がってくる移動を示している。この青色部分にかかる時間と同じ時間をかけてa階に下がってくる移動を赤色部分で示している。

図1は、ある位置からa階に単純に下がってくるケース。青色部分が短い場合に起こりやすい。

図2は、ある位置から最上階のb階に上がってから、a階に下がってくるケース。青色部分が長い場合に起こりやすい。

どちらの図でも、a階より上の空間にいるエレベーターは、ある位置からａ階までの赤色部分にエレベーターがいること、それがa階より下の空間にいるエレベーターより先にa階に来るために必要となる。

図のように、青色部分をα区間、赤色部分をβ区間、緑色部分をγ区間と呼ぶことにしよう。α区間の移動とβ区間の移動に要する時間は、同じということになる。

ここで、エレベーターがα区間にいる確率も、β区間にいる確率も、(a-1)/(b-1)、つまりpだ。

a階にどちらが先に来るかという競争の結果は、五分五分だ。このため、1)がa階より上の空間、2)がa階より下の空間にいて、1)が先に来るケースの確率は、p²/2となる。

1)と2)の立場を置き換えて、2)がa階より上の空間、1)がa階より下の空間にいて、2)が先に来るケースの確率も、p²/2となる。結局、(2)の確率は、p²/2 ＋p²/2＝p²となる。

エレベーターの数が2台の場合は、(1)と(2)の確率を合計して、

(1-p)² ＋ p² ＝ 1 － 2p ＋ 2p²

となる。これは、1/2 ＋ 1/2 × (1-2p)² と表すことができる。これが、次に来るエレベーターが下向きである確率となる。

7階建のビルの2階で待っているケースでは、p＝1/6なので、次に来るエレベーターが下向きである確率は13/18となる。エレベーターが1台の場合の確率5/6に比べて、少し小さくなっている。

日付	タイトル	執筆者	媒体
2025/04/28	リスクアバースの原因－やり直しがきかないとリスクはとれない	篠原拓也	研究員の眼
2025/04/22	審査の差の定量化－審査のブレはどれくらい?	篠原拓也	研究員の眼
2025/04/15	患者数:入院は減少、外来は増加－2023年の「患者調査」にコロナ禍の影響はどうあらわれたか?	篠原拓也	基礎研レター
2025/04/08	センチネル効果の活用－監視されていると行動が改善する?	篠原拓也	研究員の眼

日付

タイトル

執筆者

媒体

2025/04/28

リスクアバースの原因－やり直しがきかないとリスクはとれない

篠原拓也

研究員の眼

2025/04/22

審査の差の定量化－審査のブレはどれくらい?

篠原拓也

研究員の眼