- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 数学記号の由来について(10)-確率・統計(P、E、nPr、nCr、μ、σ等)-
コラム
2021年11月24日
文字サイズ
- 小
- 中
- 大
はじめに
何回かに分けて、これまで慣れ親しんできた数学で使用されている記号の由来について、報告している1。
第1回目は、四則演算の記号(+、-、×、÷)の由来について、第2回目は、数字の関係を表す記号(=、≒、<、>等)について、第3回目は、集合論で使用される記号(∩、∪、⊂、⊃等)について、第4回目は、論理記号(∀、∃、∴、∵等)、第5回は、べき乗(an)、平行根(√) 等、第6回は、無限大(∞)、比例(∝)、相似(∽)等、第7回は、三角関数(sin、cos、tan等)、第8回は、「数」の記号、第9回は、数学定数等(e、π、φ、i)について報告した。
今回は、確率・統計からの記号についてということで、P(確率)、E(期待値)、nPr(順列)、nCr(組み合わせ)、μ(平均)、σ(標準偏差)等について報告する。
1 主として、以下の文献を参考にした。
Florian Cajori「A History of Mathematical Notations」(1928、1929)の冊子の再発行版(2012)(Dover Publications,Inc)
第1回目は、四則演算の記号(+、-、×、÷)の由来について、第2回目は、数字の関係を表す記号(=、≒、<、>等)について、第3回目は、集合論で使用される記号(∩、∪、⊂、⊃等)について、第4回目は、論理記号(∀、∃、∴、∵等)、第5回は、べき乗(an)、平行根(√) 等、第6回は、無限大(∞)、比例(∝)、相似(∽)等、第7回は、三角関数(sin、cos、tan等)、第8回は、「数」の記号、第9回は、数学定数等(e、π、φ、i)について報告した。
今回は、確率・統計からの記号についてということで、P(確率)、E(期待値)、nPr(順列)、nCr(組み合わせ)、μ(平均)、σ(標準偏差)等について報告する。
1 主として、以下の文献を参考にした。
Florian Cajori「A History of Mathematical Notations」(1928、1929)の冊子の再発行版(2012)(Dover Publications,Inc)
確率関係
P(A):Aの確率 の使用及び由来
事象Aが発生する確率をP(A)と表現するが、確率論が何世紀にもわたって研究されてきたことに比較して、この記号の使用は比較的最近のことであったようだ。
現代的な確率論の基礎を確立したロシアの数学者であるアンドレイ・ニコラエヴィッチ・コルモゴロフ(A. N. Kolmogorov)が1933年の有名な著書「確率論の基礎概念(Grundbegriffe der Wahrscheinlichkeitsrechnung )」で使用した。「P」は「probability」の頭文字である。また、事象Aに対する大文字の使用は、集合論からきているようだ。
事象Aが発生する確率をP(A)と表現するが、確率論が何世紀にもわたって研究されてきたことに比較して、この記号の使用は比較的最近のことであったようだ。
現代的な確率論の基礎を確立したロシアの数学者であるアンドレイ・ニコラエヴィッチ・コルモゴロフ(A. N. Kolmogorov)が1933年の有名な著書「確率論の基礎概念(Grundbegriffe der Wahrscheinlichkeitsrechnung )」で使用した。「P」は「probability」の頭文字である。また、事象Aに対する大文字の使用は、集合論からきているようだ。
P(A|B)又はPB(A):条件Bの下でのAの確率 の使用及び由来
ある事象Bが発生するという条件下で別の事象Aが発生する確率のことを「条件付き確率(conditional probability)」といい、P(A|B)又はPB(A)といった記号で表す。
A. N. コルモゴロフは先の1933年の著書の中でPB(A)を使用したが、英国の数学者であるハロルド・ジェフリーズ(Harold Jeffreys)によって以前に使用されていたP(A|B)の記法が、クロアチア生まれの米国の数学者であるウイリアム・フェラー(William Feller)が1950年に使用したことによって普及してきたようだ。また、スウェーデンの数学者でアクチュアリーであったハラルド・クラメル(Harald Cramér)は1937年に「相対確率(relative probability)」と呼んでいたが、ロシアの数学者であるジェームズ・ビクター・ウスペンスキー(James Victor Uspensky)が同じく1937年に「条件付き確率(conditional probability)」という用語を使用した。
なお、英語では「probability of A under the condition B」又は「probability of A given B」と表現される。
ある事象Bが発生するという条件下で別の事象Aが発生する確率のことを「条件付き確率(conditional probability)」といい、P(A|B)又はPB(A)といった記号で表す。
A. N. コルモゴロフは先の1933年の著書の中でPB(A)を使用したが、英国の数学者であるハロルド・ジェフリーズ(Harold Jeffreys)によって以前に使用されていたP(A|B)の記法が、クロアチア生まれの米国の数学者であるウイリアム・フェラー(William Feller)が1950年に使用したことによって普及してきたようだ。また、スウェーデンの数学者でアクチュアリーであったハラルド・クラメル(Harald Cramér)は1937年に「相対確率(relative probability)」と呼んでいたが、ロシアの数学者であるジェームズ・ビクター・ウスペンスキー(James Victor Uspensky)が同じく1937年に「条件付き確率(conditional probability)」という用語を使用した。
なお、英語では「probability of A under the condition B」又は「probability of A given B」と表現される。
E(期待値)の使用及び由来
「E」は、英語の期待値を意味する「Expected Value」の頭文字を表している。この「E」は、英国の数学者であるウイリアム・アレン・ウィットワース(William Allen Whitworth)の1901年の有名な教科書Choice and Chance(第5版)で使用されたが、英語圏ではその後ずっと後になるまで確立されず、むしろ欧州大陸で多く使用されてきたようだ。ただし、欧州大陸でのEは、同じく期待を意味している「Erwartung(ドイツ語)」や「éspérance(フランス語)」に由来している。
「E」は、英語の期待値を意味する「Expected Value」の頭文字を表している。この「E」は、英国の数学者であるウイリアム・アレン・ウィットワース(William Allen Whitworth)の1901年の有名な教科書Choice and Chance(第5版)で使用されたが、英語圏ではその後ずっと後になるまで確立されず、むしろ欧州大陸で多く使用されてきたようだ。ただし、欧州大陸でのEは、同じく期待を意味している「Erwartung(ドイツ語)」や「éspérance(フランス語)」に由来している。
F(分布関数)、f(密度関数)の使用及び由来
一般的な分布関数(Distribution function)にFを使用することは、1920年代から確率分布の文献で確立されていたようだ。
一方で、フランスの数学者であるポール・レヴィ(Paul Lévy)は密度関数にfを使用し、ハラルド・クラメルは1937年に、Fに対応する特性関数にfを使用した。1940年代以降、分布関数のFと密度関数のf (これらの役割で大文字と対応する小文字を使用するというより広い規則の範囲内)は、英国の統計学者であるモーリス・ケンダール(Maurice Kendall )と米国の数学者であるサミュエル・スタンレー・ウイルクス(Samuel Stanley Wilks)の論文に従って、特に統計学者によって広く採用されてきたようだ。
一般的な分布関数(Distribution function)にFを使用することは、1920年代から確率分布の文献で確立されていたようだ。
一方で、フランスの数学者であるポール・レヴィ(Paul Lévy)は密度関数にfを使用し、ハラルド・クラメルは1937年に、Fに対応する特性関数にfを使用した。1940年代以降、分布関数のFと密度関数のf (これらの役割で大文字と対応する小文字を使用するというより広い規則の範囲内)は、英国の統計学者であるモーリス・ケンダール(Maurice Kendall )と米国の数学者であるサミュエル・スタンレー・ウイルクス(Samuel Stanley Wilks)の論文に従って、特に統計学者によって広く採用されてきたようだ。
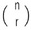 (二項係数)の使用及び由来
(二項係数)の使用及び由来 「二項係数(binomial coefficients)」というのは、二項展開(二項式の冪(べき)の展開)において係数として現れる正の整数のことをいい、通常
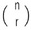 で表記される。
で表記される。「二項係数」については、パスカルの三角形が有名だが、それよりも何世紀も前の数学者達によって研究されてきた。レオンハルト・オイラー(Leonhard Euler)が1778年に書いた論文でnとrをカッコ内に記述する(ただし、水平分数線付き)記号を採用したが、これは1806年まで公表されなかった。彼は、1781年に書き、1784年に公表した論文ではカッコを除いて同じ記法を使用していた。
現在の表記であるnとrをカッコ内に記述する(水平分数線無し)
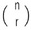 という方式は、1826年にオーストリアの数学者であるアンドレアス・フォン・エッチンクハウゼン(Andreas von Ettingshausen)による論文の中に見られ、1827年の「Vorlesungen über höhere Mathematik, Vol. I」の中で導入された。
という方式は、1826年にオーストリアの数学者であるアンドレアス・フォン・エッチンクハウゼン(Andreas von Ettingshausen)による論文の中に見られ、1827年の「Vorlesungen über höhere Mathematik, Vol. I」の中で導入された。なお、二項係数については、その他に以下の組み合わせで使用する「nCr」や「C(n,k)」等といった表記がされることもある。
ここで使用される「!」(階乗)記号の使用と由来については、研究員の眼「数学記号の由来について(5)-べき乗(an)、平方根(√) 等-」(2020.7.7)で説明したので、そちらを参照していただくことにして、今回は上記の記号の使用と由来について報告する。
「nPr」における「P」は、英語の順列を意味する「Permutation」の頭文字を表している。「nPr」という表示は、ハーベイ・グッドウィン(Harvey Goodwin)が1869年頃から使用しだしたとされ、彼の「Elementary Course of Mathematics」の第3版に現れている。
一方で、「nCr」における「C」は、英語の組み合わせを意味する「Combination」の頭文字を表している(選択を意味する「Choice」を表しているという説もある)。「nCr」という表示は、ジョージ・クリスタル(George Chrystal)が1899年の「Algebra, Part II」の中で使用している。
「nPr」における「P」は、英語の順列を意味する「Permutation」の頭文字を表している。「nPr」という表示は、ハーベイ・グッドウィン(Harvey Goodwin)が1869年頃から使用しだしたとされ、彼の「Elementary Course of Mathematics」の第3版に現れている。
一方で、「nCr」における「C」は、英語の組み合わせを意味する「Combination」の頭文字を表している(選択を意味する「Choice」を表しているという説もある)。「nCr」という表示は、ジョージ・クリスタル(George Chrystal)が1899年の「Algebra, Part II」の中で使用している。
(参考)順列、組み合わせのその他のパターン
ここで、実際の応用で役立つ、順列、組み合わせのその他の代表的なパターンの公式を示しておく。学生時代に試験対策等で覚えた記憶がある方も多いと思われるが、頭の整理になると思われることから、簡単な説明とともに掲げておくことにする。
1.重複順列
(通常の順列は重複を許さないものであるが)異なる n 個の中から、重複を許して r 個を取り出し、1 列に並べる場合の数は、毎回n個のいずれも並べることができることから、nr となる。
2.円順列
異なる n 個のものを円形に並べる順列の場合の数は、1個の位置を固定して通常の順列を考えればよいので、(n−1)! となる。
3.数珠順列
異なる n 個のものの数珠順列(円順列で裏返しによって同じ並び方になるものを同一視する)の場合の数は、円順列の場合の数の半分になるので、(n−1)!/2 となる。
4.重複組み合わせ
異なる n 個のものから重複を許して r 個を選ぶ組み合わせの総数については、「r 個のものと (n−1) 個の仕切りを一列に並べる方法」と同じ場合の数になる。
この考え方は、最初はなかなかわかりにくいと思われる。通常の発想では、まずは異なるn個のイメージがあって、それからどうやってr個を選ぶのかということになるが、この考え方はある意味で発想の転換をして、選ぶr個が先にありきで、それをいかに異なるn個に区分していくのかという考え方をする。この考え方によれば、r個をn個の異なるものに分けるために、(n-1)個の仕切りが必要ということになる。
具体的に、異なる3個の中から5個取り出すことを考えると、以下のような感じになる。
選択する5個を 〇 〇 〇 〇 〇 のように並べるとする。
これを異なる3種類に区分するためには、上記5個のどこかに2つの仕切りを入れてやればよい。具体的には、以下の通りである。
〇 〇|〇 〇|〇
〇|〇 〇 〇|〇
〇 〇 〇|〇 〇| (3種類目は1つも選ばれないことを意味している)
こうした選び方の総数は、結局(n+r-1)個の中から、r個を取り出す組み合わせの数に等しくなる。即ち、求める総数は、
nHr = n+r−1Cr
となる。因みに、「H」は、英語の「homogeneous」(同種の)の頭文字である。
5.同じものを含む順列
n 個のもののうち、p個、q個、r個……(n=p+q+r+……)が同じものであるとき、それらのn個のもの全てを一列に並べる順列の数は、
ここで、実際の応用で役立つ、順列、組み合わせのその他の代表的なパターンの公式を示しておく。学生時代に試験対策等で覚えた記憶がある方も多いと思われるが、頭の整理になると思われることから、簡単な説明とともに掲げておくことにする。
1.重複順列
(通常の順列は重複を許さないものであるが)異なる n 個の中から、重複を許して r 個を取り出し、1 列に並べる場合の数は、毎回n個のいずれも並べることができることから、nr となる。
2.円順列
異なる n 個のものを円形に並べる順列の場合の数は、1個の位置を固定して通常の順列を考えればよいので、(n−1)! となる。
3.数珠順列
異なる n 個のものの数珠順列(円順列で裏返しによって同じ並び方になるものを同一視する)の場合の数は、円順列の場合の数の半分になるので、(n−1)!/2 となる。
4.重複組み合わせ
異なる n 個のものから重複を許して r 個を選ぶ組み合わせの総数については、「r 個のものと (n−1) 個の仕切りを一列に並べる方法」と同じ場合の数になる。
この考え方は、最初はなかなかわかりにくいと思われる。通常の発想では、まずは異なるn個のイメージがあって、それからどうやってr個を選ぶのかということになるが、この考え方はある意味で発想の転換をして、選ぶr個が先にありきで、それをいかに異なるn個に区分していくのかという考え方をする。この考え方によれば、r個をn個の異なるものに分けるために、(n-1)個の仕切りが必要ということになる。
具体的に、異なる3個の中から5個取り出すことを考えると、以下のような感じになる。
選択する5個を 〇 〇 〇 〇 〇 のように並べるとする。
これを異なる3種類に区分するためには、上記5個のどこかに2つの仕切りを入れてやればよい。具体的には、以下の通りである。
〇 〇|〇 〇|〇
〇|〇 〇 〇|〇
〇 〇 〇|〇 〇| (3種類目は1つも選ばれないことを意味している)
こうした選び方の総数は、結局(n+r-1)個の中から、r個を取り出す組み合わせの数に等しくなる。即ち、求める総数は、
nHr = n+r−1Cr
となる。因みに、「H」は、英語の「homogeneous」(同種の)の頭文字である。
5.同じものを含む順列
n 個のもののうち、p個、q個、r個……(n=p+q+r+……)が同じものであるとき、それらのn個のもの全てを一列に並べる順列の数は、
となる。
統計関係
フランスの数学者であるピエール=シモン・ラプラス(Pierre-Simon Laplace)やドイツの数学者であるヨハン・カール・フリードリヒ・ガウス(Johann Carl Friedrich Gauß)といった18世紀から19世紀にかけての巨匠やその後継者等によって使用されてきた表記法は、いずれも現在の統計にはあまり生き残っていないようである。現在の表記法は、20世紀初頭の主要な英国の統計学者であったカール・ピアソン(Karl Pearson)や同じく英国の統計学者で遺伝学者であったR.A.フィッシャー(Sir Ronald Aylmer Fisher)が多くの基本的な記号と原則を導入した1890年から1940年代に由来しているようである。
「μ」(平均)の使用及び由来
正規分布の平均を表す記号として「μ」が使用される。この「μ」はギリシア文字の「m」であり、平均のことを英語では「mean」と言うが、ギリシア語では「μέση τιμή」となる。
因みに、平均を表す英語としては「average」という用語があり、こちらの方が一般的だと思われるが、「mean」は統計用語で使用されてきている。「mean」は算術的平均を指しているが、「average」は算術的平均を含んだ、より幅広い意味での平均を表しており、統計における「中央値(median)」、「モード(mode)」、「ミッドレンジ(mid-range)」といった概念も含まれることになる。
µの使用が確立されたのは、極めて最近で、遺伝学と生物数学における統計学の使用を開発する上で重要な役割を果たしたR.A.フィッシャーが1936年の「Statistical Methods for Research Workers」の第6版で採用した。彼は、1912年からmを使用し、標本平均には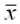 を使用していたようだ。
を使用していたようだ。
正規分布の平均を表す記号として「μ」が使用される。この「μ」はギリシア文字の「m」であり、平均のことを英語では「mean」と言うが、ギリシア語では「μέση τιμή」となる。
因みに、平均を表す英語としては「average」という用語があり、こちらの方が一般的だと思われるが、「mean」は統計用語で使用されてきている。「mean」は算術的平均を指しているが、「average」は算術的平均を含んだ、より幅広い意味での平均を表しており、統計における「中央値(median)」、「モード(mode)」、「ミッドレンジ(mid-range)」といった概念も含まれることになる。
µの使用が確立されたのは、極めて最近で、遺伝学と生物数学における統計学の使用を開発する上で重要な役割を果たしたR.A.フィッシャーが1936年の「Statistical Methods for Research Workers」の第6版で採用した。彼は、1912年からmを使用し、標本平均には
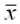 を使用していたようだ。
を使用していたようだ。
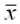 (標本平均)の使用及び由来
(標本平均)の使用及び由来標本平均を表すのに、xの上に「-(バー)」を付ける表記は、あらゆる種類の平均をバーで表す応用数学者の実践に由来しているようだ。物理学で平均速度を表すのに
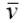 、慣性中心を表すのに
、慣性中心を表すのに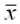 を使用していたが、カール・ピアソンがこうした物理学の背景を有していたことから、カール・ピアソンと彼の同世代の人々は標本平均と期待値にバーを使用していた。期待値については、先に述べたようにEに代わっていったが、
を使用していたが、カール・ピアソンがこうした物理学の背景を有していたことから、カール・ピアソンと彼の同世代の人々は標本平均と期待値にバーを使用していた。期待値については、先に述べたようにEに代わっていったが、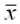 については、R.A.フィッシャーが影響力ある形で使用していたことから、そのまま生き残ってきたようだ。
については、R.A.フィッシャーが影響力ある形で使用していたことから、そのまま生き残ってきたようだ。
「σ」(標準偏差)や「σ2」(分散)の使用及び由来
正規分布の標準偏差を表す記号として「σ」が使用されるが、この「σ」はギリシア文字の「s」であり、標準偏差のことを英語で「standard variation」あるいは「standard deviation」と言うことに由来している。
標準偏差に最初のσを使用したのは、1894年のカール・ピアソンの論文「Contributions to the Mathematical Theory of Evolution」においてであった。R.A.フィッシャーが1918年に分散(variance)を導入した時に、彼はσ2を使用した。ピアソンはパラメータと推定値を区別しなかったが、英国の統計学者であるウイリアム・ゴセット(William Gosset)はその「The Probable Error of a Mean」の中で、σの推定値としてsを使用した。ただし、分母は現在の実務における(n-1)ではなくてnだったとのことである。、あた、R.A.フィッシャーは彼の1922年の論文でσ2の推定値としてs2を使用したようだ。
正規分布の標準偏差を表す記号として「σ」が使用されるが、この「σ」はギリシア文字の「s」であり、標準偏差のことを英語で「standard variation」あるいは「standard deviation」と言うことに由来している。
標準偏差に最初のσを使用したのは、1894年のカール・ピアソンの論文「Contributions to the Mathematical Theory of Evolution」においてであった。R.A.フィッシャーが1918年に分散(variance)を導入した時に、彼はσ2を使用した。ピアソンはパラメータと推定値を区別しなかったが、英国の統計学者であるウイリアム・ゴセット(William Gosset)はその「The Probable Error of a Mean」の中で、σの推定値としてsを使用した。ただし、分母は現在の実務における(n-1)ではなくてnだったとのことである。、あた、R.A.フィッシャーは彼の1922年の論文でσ2の推定値としてs2を使用したようだ。
「ρ」(相関係数)の使用及び由来
「相関」の英語は「correlation」だが、相関の概念を発見したフランシス・ゴㇽトン(Frnacis Galton)が、相関係数を表すために回帰直線(regression line)を使用したことから、「regression」の頭文字の「r」のギリシア文字の「ρ」が使用されている。
英国の遺伝学者で、統計学の祖とも呼ばれるフランシス・ゴㇽトンは、1888年の「Co-Relations and Their Measurement」の中で、相関の指標のために、恐らくその回帰との類似性から「r」の記号を使用した。「ρ」の使用は1892年の英国の経済学者であるフランシス・エッジワース(Francis Edgeworth) の「Correlated Averages」の中に見られたとのことである。
英国の統計学者のジョージ・ウドニー・ユール(George Udny Yule)は、1907年にx1、x2、x3の間の部分相関に対して、r1,2,3 という記号を導入した。そのギリシア文字版のρ1,2,3 という記号は、1933年に英国の統計学者であるモーリス・スチーブンソン・バートレット(Maurice Stevenson Bartlett) によって使用された。
Rが、少なくとも1896年のYuleの使用から、重相関係数(multiple correlation coefficient)に対して使用されてきたが、今は一般的には標本係数に対して使用されている。
なお、回帰の行列表記については、1920年代に最初に使用されたが、1950年代になってから幅広く使用されるようになった。
「相関」の英語は「correlation」だが、相関の概念を発見したフランシス・ゴㇽトン(Frnacis Galton)が、相関係数を表すために回帰直線(regression line)を使用したことから、「regression」の頭文字の「r」のギリシア文字の「ρ」が使用されている。
英国の遺伝学者で、統計学の祖とも呼ばれるフランシス・ゴㇽトンは、1888年の「Co-Relations and Their Measurement」の中で、相関の指標のために、恐らくその回帰との類似性から「r」の記号を使用した。「ρ」の使用は1892年の英国の経済学者であるフランシス・エッジワース(Francis Edgeworth) の「Correlated Averages」の中に見られたとのことである。
英国の統計学者のジョージ・ウドニー・ユール(George Udny Yule)は、1907年にx1、x2、x3の間の部分相関に対して、r1,2,3 という記号を導入した。そのギリシア文字版のρ1,2,3 という記号は、1933年に英国の統計学者であるモーリス・スチーブンソン・バートレット(Maurice Stevenson Bartlett) によって使用された。
Rが、少なくとも1896年のYuleの使用から、重相関係数(multiple correlation coefficient)に対して使用されてきたが、今は一般的には標本係数に対して使用されている。
なお、回帰の行列表記については、1920年代に最初に使用されたが、1950年代になってから幅広く使用されるようになった。
N(µ、σ2):平均µ、分散σ2の正規分布 の歴史
「正規分布(normal distribution)」は300年近く前から研究されており、多くの表記が使用されてきたが、今日使用されているものは比較的最近のものであるようだ。
正規分布は、1733年に、フランスの数学者であるアブラーム・ド・モアブル(Abraham de Moivre)によって導入された。ド・モアブルの結果は、同じくフランスの数学者であるピエール=シモン・ラプラスによって発展させられて、「ド・モアブル–ラプラスの定理」と呼ばれるものとなっている。これは、中心極限定理の特別な場合に相当しており、「二項分布B(n,p)はn が十分大きいとき、平均np、分散np(1-p)の正規分布に近づく2」あるいはその標準化されたものでは「確率変数Xが二項分布B(n,p)に従うとき、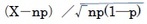 は近似的に標準正規分布に従う)というものである。
は近似的に標準正規分布に従う)というものである。
1809年には、カール・フリードリヒ・ガウが、誤差論という別のアプローチから、正規分布について詳細に分析した。正規分布は「ガウス分布」とも呼ばれる。
なお、「正規分布」という用語は、先に述べたフランシス・ゴルトン、米国の哲学者、論理学者、数学者で、プラグマティズムの創始者として知られるチャールズ・サンダース・パース(Charles Sanders Peirce)及びドイツの経済学者で統計学者であるヴィルヘルム・レキシ(Wilhelm Lexis)の3人によって1875年頃に独立に導入されたようである。また、「標準正規(standard normal)」という用語は1950年頃に一般的に使用されるようになっている。
2 「二項分布」は、成功確率 p が一定の試行(ベルヌーイ試行)を独立に n 回行ったときの成功回数を確率変数とする離散確率分布である。
「正規分布(normal distribution)」は300年近く前から研究されており、多くの表記が使用されてきたが、今日使用されているものは比較的最近のものであるようだ。
正規分布は、1733年に、フランスの数学者であるアブラーム・ド・モアブル(Abraham de Moivre)によって導入された。ド・モアブルの結果は、同じくフランスの数学者であるピエール=シモン・ラプラスによって発展させられて、「ド・モアブル–ラプラスの定理」と呼ばれるものとなっている。これは、中心極限定理の特別な場合に相当しており、「二項分布B(n,p)はn が十分大きいとき、平均np、分散np(1-p)の正規分布に近づく2」あるいはその標準化されたものでは「確率変数Xが二項分布B(n,p)に従うとき、
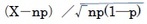 は近似的に標準正規分布に従う)というものである。
は近似的に標準正規分布に従う)というものである。1809年には、カール・フリードリヒ・ガウが、誤差論という別のアプローチから、正規分布について詳細に分析した。正規分布は「ガウス分布」とも呼ばれる。
なお、「正規分布」という用語は、先に述べたフランシス・ゴルトン、米国の哲学者、論理学者、数学者で、プラグマティズムの創始者として知られるチャールズ・サンダース・パース(Charles Sanders Peirce)及びドイツの経済学者で統計学者であるヴィルヘルム・レキシ(Wilhelm Lexis)の3人によって1875年頃に独立に導入されたようである。また、「標準正規(standard normal)」という用語は1950年頃に一般的に使用されるようになっている。
2 「二項分布」は、成功確率 p が一定の試行(ベルヌーイ試行)を独立に n 回行ったときの成功回数を確率変数とする離散確率分布である。
最後に
今回は、確率・統計からの記号についてということで、P(確率)、E(期待値)、nPr(順列)、nCr(組み合わせ)、μ(平均)、σ(標準偏差)等について報告してきた。確率・統計においては、今回紹介したもの以外にも数多くの記号が使用されているが、今回は基本的なものだけに留めている。
確率・統計については、他の数学分野に比べて、身近に接する機会も多く、なじみ深い記号も多いものと思われる。確率等については、古くから研究されてきており、著名な大数学者達が多くの結果を残してきている。ただし、その数学記号については、必ずしもそれらの大数学者達が使用してきたものがそのまま現代まで生き残って使用されてきているとは限らないようである。
その意味で、数学記号の普及・定着というのは、あまり単純なものではなく、結構複雑な歴史や経緯を有しているものだと改めて感じさせられる。
確率・統計については、他の数学分野に比べて、身近に接する機会も多く、なじみ深い記号も多いものと思われる。確率等については、古くから研究されてきており、著名な大数学者達が多くの結果を残してきている。ただし、その数学記号については、必ずしもそれらの大数学者達が使用してきたものがそのまま現代まで生き残って使用されてきているとは限らないようである。
その意味で、数学記号の普及・定着というのは、あまり単純なものではなく、結構複雑な歴史や経緯を有しているものだと改めて感じさせられる。
(2021年11月24日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
| 2025/09/25 | 数字の「49」に関わる各種の話題-49という数字に皆さんはどんなイメージを有しているのだろう- | 中村 亮一 | 研究員の眼 |
| 2025/09/12 | 数字の「48」に関わる各種の話題-48という数字は、結構いろいろな場面で現れてくるようだ- | 中村 亮一 | 研究員の眼 |
新着記事
-
2025年10月14日
今週のレポート・コラムまとめ【10/7-10/10発行分】 -
2025年10月10日
企業物価指数2025年9月~国内企業物価の上昇率は前年比2.7%、先行きは鈍化予想~ -
2025年10月10日
中期経済見通し(2025~2035年度) -
2025年10月10日
保険・年金関係の税制改正要望(2026)の動き-関係する業界・省庁の改正要望事項など -
2025年10月10日
若者消費の現在地(4)推し活が映し出す、複層的な消費の姿~データで読み解く20代の消費行動
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【数学記号の由来について(10)-確率・統計(P、E、nPr、nCr、μ、σ等)-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
数学記号の由来について(10)-確率・統計(P、E、nPr、nCr、μ、σ等)-のレポート Topへ




















 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




