- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 絶対値をとるか、二乗するか-機械学習での評価方法は誰が決める?
絶対値をとるか、二乗するか-機械学習での評価方法は誰が決める?

保険研究部 主席研究員 兼 気候変動リサーチセンター チーフ気候変動アナリスト 兼 ヘルスケアリサーチセンター 主席研究員 篠原 拓也
― 生成AIで「フィッシングサイト」識別 警察庁が2025年度までに導入へ (毎日新聞 2024.3.21)
― 公的機関のAI活用例、世界で共有 G7デジタル相会合 (朝日新聞デジタル 2024.3.16)
― 世界初のAI規制法、EU議会で可決 制裁金最大56億円 (Forbes Japan 2024.3.14)
― 米新興企業のAI投資3.7兆円に ロボや医療に裾野拡大 (日本経済新聞 2024.3.12)
といった感じだ。いま、世の中は「AI全盛時代」を迎えつつあるのかもしれない。
AIと言えば機械学習だ。AIは、まず、データをもとに機械学習をする。そして、与えられたデータを分類したり、与えられたデータをもとに予測をしたりする。通常、多くのデータで機械学習をしていけば、分類や予測の精度は高まっていく。2022年に登場した生成AIは、文章や画像などのコンテンツを作り出す。まさに、人工の“知能”と呼ぶのにふさわしい発展を続けている。
機械学習のうち予測に関するものは、以前から「回帰分析」として行われてきたものの、大幅な拡張と見ることができる。予測の機械学習では、どれくらい予測があたったか、の評価が重要となる。
今回は、予測の機械学習における評価について、考えてみることとしたい。
◇ 予測と正解の誤差 ― 絶対値をとるか、二乗するか
ただし、誤差を単純な引き算として計算すると、一般に、複数の予測のうち、ある箇所のプラスの誤差と、別のある箇所のマイナスの誤差が相殺し合って誤差の合計が小さくなってしまう。
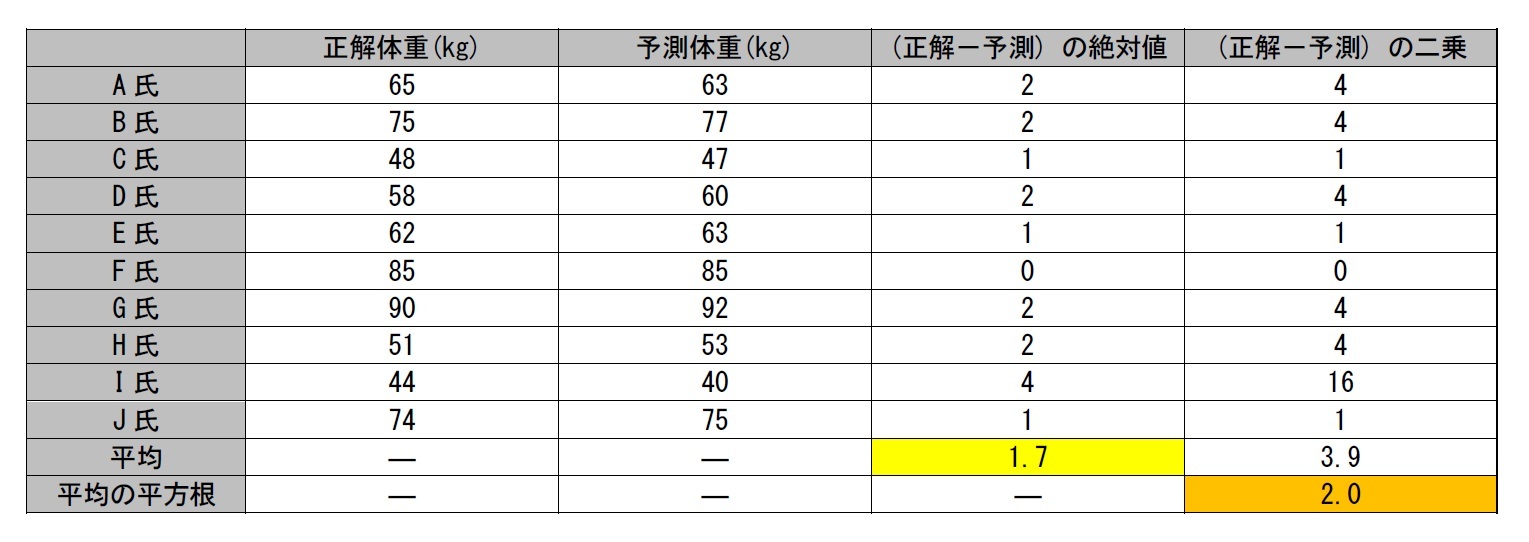
そこで、単純な引き算ではなく、引き算した結果のマイナスの値をプラスに変換するような計算が必要となる。そこで考えつくのが、(1) 誤差の絶対値をとる方法と、(2) 誤差を二乗する方法だ。
複数の予測で、誤差の絶対値をとって、その平均を計算したものは「平均絶対誤差 (Mean Absolute Error, MAE)」と呼ばれる。一方、誤差を二乗して、その平均の平方根を計算したものは「平均平方根二乗誤差 (Root Mean Squared Error, RMSE)」と呼ばれる。
RMSEとMAEはマイナスの値にはならず、どちらの評価指標も0に近いほど誤差が小さい、つまり予測の精度が高いことを意味する。数学的には、RMSE ≧ MAE (等号は複数の予測の誤差の絶対値がすべて等しい場合)となることが示される。
実は、MAEとRMSEの間では、どちらが優れた評価指標か、という議論が長らく繰り広げられてきた。
◇ RMSEは微分可能で使いやすい
このとき、評価の算式(関数)が微分可能だと、予測値を見直したときに着実に正解に近付くことができる。つまり、最適化できる。
RMSEは二乗の算式なので微分ができる。一方、MAEは絶対値をとる算式なので、誤差が0となる箇所で微分ができない。(誤差がプラスの方からこの箇所に近付くと傾きがプラス、誤差がマイナスの方から近付くと傾きがマイナスとなり、傾きが不連続となる。)
そのため、機械学習の最適化アルゴリズムの観点からはRMSEが使いやすいということになる。
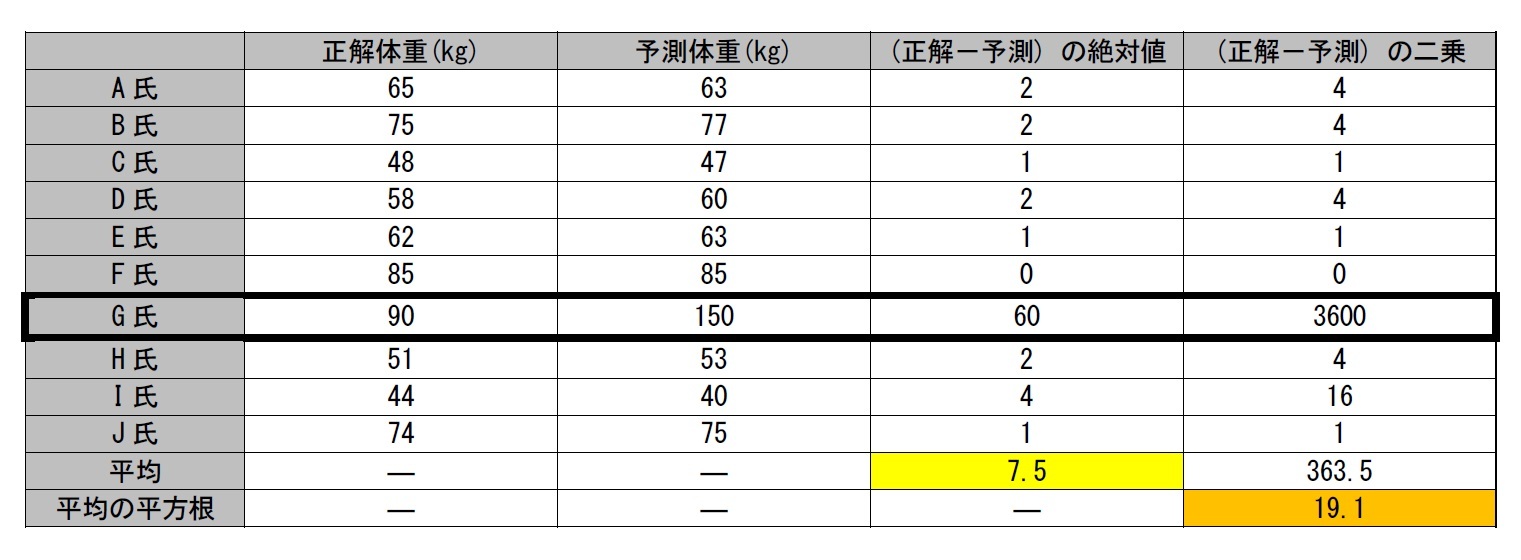
◇ MAEは外れ値に強い
(2024年04月02日「研究員の眼」)

保険研究部 主席研究員 兼 気候変動リサーチセンター チーフ気候変動アナリスト 兼 ヘルスケアリサーチセンター 主席研究員
篠原 拓也 (しのはら たくや)
研究・専門分野
保険商品・計理、共済計理人・コンサルティング業務
03-3512-1823
- 【職歴】
1992年 日本生命保険相互会社入社
2014年 ニッセイ基礎研究所へ
【加入団体等】
・日本アクチュアリー会 正会員
篠原 拓也のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2024/10/29 | 気候変動AFOLUでの取り組み-風力・太陽光発電に匹敵する緩和ポテンシャルをどう引き出すか? | 篠原 拓也 | 基礎研レター |
| 2024/10/22 | ツーポイント・コンバージョンの選択-勝利の確率を高めるために、いま勝負に打って出るべきか? | 篠原 拓也 | 研究員の眼 |
| 2024/10/15 | 超過確率何分の1の豪雨が基準?-治水事業の整備基準を確率の面から見てみよう | 篠原 拓也 | 研究員の眼 |
| 2024/10/08 | タブー・トレードオフへの対処-環境問題への取り組みには心理学の知見も必要!? | 篠原 拓也 | 研究員の眼 |
公式SNSアカウント
新着レポートを随時お届け!日々の情報収集にぜひご活用ください。
新着記事
-
2024年10月31日
首都圏新築マンション市場の動向(2024年9月)~マンション発売戸数は今後も低水準にとどまる見通し -
2024年10月31日
2024年7-9月期の実質GDP~前期比0.2%(年率0.8%)を予測~ -
2024年10月31日
なぜ「今」BeRealを撮影する必要があるのだろうか-BeRealに関する私論的考察 -
2024年10月31日
ユーロ圏GDP(2024年7-9月期)-前期比0.4%で成長は加速 -
2024年10月31日
米GDP(24年7-9月期)-前期比年率+2.8%と前期から小幅低下、市場予想の+2.9%も小幅に下回る
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2024年07月01日
News Release
-
2024年04月02日
News Release
-
2024年02月19日
News Release
【絶対値をとるか、二乗するか-機械学習での評価方法は誰が決める?】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
絶対値をとるか、二乗するか-機械学習での評価方法は誰が決める?のレポート Topへ


















 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!





