数字の「48」に関わる各種の話題－48という数字は、結構いろいろな場面で現れてくるようだ

数字の「48」に関わる各種の話題－48という数字は、結構いろいろな場面で現れてくるようだ－

このレポートの関連カテゴリ

バッハの平均律クラヴィーア曲集は48曲

日本においては「音楽の父」と称されるヨハン・ゼバスティアン・バッハ（Johann Sebastian Bach）（1685－1750）が作曲した「平均律クラヴィーア曲集（ドイツ語でDas Wohltemperierte Klavier、英語でThe Well-Tempered Clavier）」は、鍵盤楽器のための作品集である。第1巻と第2巻があり、それぞれ24の全ての調⁵による前奏曲とフーガで構成され、合計48曲からなっている。

第1巻の第1曲の前奏曲は、あの有名なシャルル・グノーのアヴェ・マリアの伴奏に使用されているので、多くの方々にとってもお馴染みの曲になっている。

なお、日本語では「平均律クラヴィーア曲集」と呼ばれているが、原題の「wohltemperierte」は、鍵盤楽器があらゆる調で演奏可能となるよう「良く調整された（well-tempered）」という意味を有している。

⁵ （西洋）音楽における「調」が長調と短調を併せて24種類あることについては、以前の研究員の眼「数字の「24」に関わる各種の話題－1日はなぜ24時間なのか－」(2023.9.27)で紹介した。

プトレマイオスの48星座

「プトレマイオスの48星座」あるいは正式には「プトレマイオス星座（Ptolemaic constellations）」と呼ばれるのは、2世紀の天文学者クラウディオス・プトレマイオスが作成した星表に見られる星座のことをいう。プトレマイオスの英語形 Ptolemy に由来して「トレミーの48星座」とも呼ばれる。

現在の天文学における星座の大元になっており、後に近代の天文学者によってプトレマイオスが観測できなかった南天や、星座と星座の隙間に新しい星座が付け加えられ、現在は星座の数は88になっている。

立方体の対称性

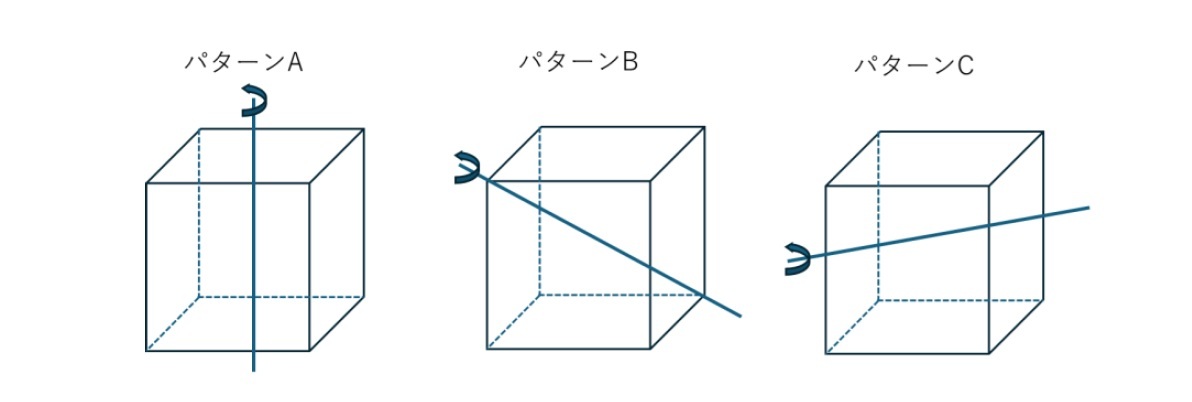
「対称性（symmetry）」というのは、ある変換に関して、変換を適用しても変わらない性質のことをいう。立方体のような空間図形の対称性については、「回転対称性」（ある図形を、特定の軸の周りに、ある回転角で回転したときに、元の図形に重なる場合）、「鏡像対称性」（ある図形を、特定の面で鏡に映したときに、元の図形と重なる場合）、「回転反転対称性」⁶（（ある図形を、特定の軸の周りに、ある回転角で回転させたのち、その軸に垂直な平面で反転⁷させたときに、元の図形に重なる場合）がある。

立方体の場合の対称性は、回転対称性が（恒等変換を含めて）24通りあるが、それ以外に、鏡面対称性が9通り、回転反転対称性が15通りの、合計48通りある。通常は、24個の回転対称変換全体が群⁸となることから、「立方体群の位数は24である」等と言われている。
具体的には、以下の通りである。

⁶ 回転反射対称性、回転鏡像対称性等とも呼ばれる。
⁷ 各点から（反転に使用する）平面に垂線を下ろし、反対側に同じ距離だけ延長した点で構成される図形への変換操作
⁸ 単位元、逆元が存在し、結合法則を満たしている集合

回転対称性
パターンA（相対する側面の中心を通る線を軸として、90°、180°、270°回転）
軸は3通りあるので、3×3の9通り

パターンB（相対する頂点を通る線を軸として、120°、240°回転）
軸は4通りあるので、2×4の8通り

パターンC（相対する稜線の中心を通る線を軸として、180°回転）
軸は6通りあるので、1×6の6通り

以上の合計に、上記に含まれていない恒等変換を加えて、24通り

鏡像対称性
パターンD（鏡を相対する側面の対角線に沿って置く場合）
1つの相対する側面の対角線は2通りあり、相対する側面は3組あるので、2×3の6通り

パターンE（鏡を相対する側面の稜線の垂直二等分線の位置に置く場合）
1つの相対する側面では1通りあり、相対する側面は3組あるので、3通り

以上の合計で、9通り

回転反転対称性
パターンF（（パターンAのように）相対する側面の中心を通る線を軸として、90°、180°、270°回転させた後、反転）
180°の回転の後に反転させるのは（立方体の中心点による）点反転⁹になるので、これを除いて、軸が3通りあることから、2×3の6通り

パターンG（（パターンBのように）相対する頂点を通る線を軸として、60°、300°回転¹⁰させた後、反転）
軸は4通りあるので、2×4の8通り

パターンH（（パターンCのように）相対する稜線の中心を通る線を軸として、180°回転させた後、反転）
180°の回転の後に反転させるのは点反転になるので、これを除くと、この軸に回転反転対称性はない。

以上の合計に、上記に含まれていない点反転変換を加えて、15通り

⁹ 固定された反転中心を挟んで全ての点が反転する変換
¹⁰ この後に反転操作があるので、パターンBの回転角とは異なることに注意が必要

その他

その他に、数字の「48」や「四十八」が現れるケースとして、例えば以下のものが挙げられる。

・「無くて七癖、有って四十八癖」：どんなに癖がないような人でも何がしらかの癖があり、癖があるような人は数多くの癖を有している。

・全国高等学校サッカー選手権大会の参加チーム数は、各都道府県の代表校（東京都代表はAとBの2校）48チームとなっている。一方で、全国高等学校野球選手権大会（いわゆる夏の甲子園）は、基本的には（記念大会等を除けば）各都道府県の代表校（東京都と北海道は2校）の49チームとなっている。

・細胞内のたんぱく質の一種である「核内受容体」は、ヒトでは48種類存在すると考えられている。

最後に

今回は数字の「48」について、それが現れてくる例やその理由等について、報告してきた。
「48」という数字は、2や3 や4や6や8といった数字で割り切れ、さらには日常生活の中で良く現れてくる数字の12や24の倍数にもなっていることから、ある意味では、何かと便利な数字だと考えることができるかもしれない。

今回のレポートで紹介した例も、相撲の「四十八手」は4種類の決まり手のそれぞれで12個が選ばれており、花札のカードの枚数は12か月の各月にそれぞれ4枚となっており、AKB48のメンバー数やバッハの平均律クラヴィーア曲数も24の2倍として、結果的に「48」という数字が現れる形になっているといえるだろう。さらには「48」が縁起の良い数字だというのも4や6や8の倍数となっていることと関係している。

一方で、古くは「48」という数字は、かなり大きいとの印象を与える数字だったようで、実際に「非常に多い」とか「多種多様な」という意味合いを示すために使用されていたようだ。

「48」という数字も、結構興味深い数字だと感じていただければと思っている。

日付	タイトル	執筆者	媒体
2025/09/12	数字の「48」に関わる各種の話題－48という数字は、結構いろいろな場面で現れてくるようだ－	中村亮一	研究員の眼
2025/09/02	欧州大手保険グループの2025年上期末SCR比率等の状況－ソルベンシーII等に基づく数値結果報告と資本管理等に関係するトピック－	中村亮一	基礎研レポート
2025/08/20	曲線にはどんな種類があって、どう社会に役立っているのか（その12）－螺旋と渦巻の応用－	中村亮一	研究員の眼
2025/08/07	複素数について（その３）－複素数の工学・物理学への応用－	中村亮一	研究員の眼

日付

タイトル

執筆者

媒体

2025/09/12

数字の「48」に関わる各種の話題－48という数字は、結構いろいろな場面で現れてくるようだ－

中村亮一

研究員の眼

2025/09/02

欧州大手保険グループの2025年上期末SCR比率等の状況－ソルベンシーII等に基づく数値結果報告と資本管理等に関係するトピック－

中村亮一

基礎研レポート