- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 分数について(その4)-分数は日常生活や社会でどのように使われているのか-
コラム
2023年04月28日
文字サイズ
- 小
- 中
- 大
はじめに
数学において分数が現れてくる例
学生時代の数学の勉強においては、小数を使用する機会は比較的限られているが、分数は多くの場面で 使用されているとの印象がある。具体的には、例えば以下のケースにおいて、分数が頻繁に現れてくる。
確率
確率を表すのには、通常は分数が使用される。ただし、実際にその確率の大きさを認識するためには、分数を小数化することが行われているものと思われる。
そもそも「確率」自体が、
何らかの出来事が起こる場合の数/全ての場合の数
という形で表現されることが多いことから、基本的には、結果は分数で表現され、答えが有限小数等になる場合のみ、小数で表現されることになる。
代表的な例として、組み合わせの確率について、例えば「m個の赤い球とn個の白い球の中から、p個(≦m)の赤い球とq(≦n)個の白い球が取り出される確率」は、以下のように分数形式で表現されることになる。
P=(mCp×nCq)/m+nCp+q
そもそも「確率」自体が、
何らかの出来事が起こる場合の数/全ての場合の数
という形で表現されることが多いことから、基本的には、結果は分数で表現され、答えが有限小数等になる場合のみ、小数で表現されることになる。
代表的な例として、組み合わせの確率について、例えば「m個の赤い球とn個の白い球の中から、p個(≦m)の赤い球とq(≦n)個の白い球が取り出される確率」は、以下のように分数形式で表現されることになる。
P=(mCp×nCq)/m+nCp+q
三角関数・三角比
音楽の音律
「音律」というのは、音階のそれぞれの音を調律する基準であり、音高の相対的な関係の規定のことを言う。楽器の調律では、基準となる特定の音の音高を定め、それから音律に従って他の音の音高を決定する。この音律には、歴史上様々なものが使用されてきており、代表的なものとして、「平均律(Equal temperament)」、「純正律(Just intonation)」、「ピタゴラス音律(Pythagorean tuning)」等がある。
このうちの「平均律」は、1オクターヴなどの音程を均等な周波数比で分割した音律で、現在の西洋音楽で使用されている「十二平均律」は、隣り合う音(半音)の周波数比が常に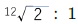 となる。
となる。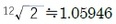 なので、音が一つ高くなると、周波数は約1.06倍になることになる1。これについては、以前の研究員の眼「「対数」に、もう一度興味・関心を持ってみませんか(その3)-対数はどこで役に立っているのか-」(2021.10.8)で紹介した。この「平均律」は(無理数による)等比数列に基づいているが、各音を表すのに指数表記が使用されることになる。
なので、音が一つ高くなると、周波数は約1.06倍になることになる1。これについては、以前の研究員の眼「「対数」に、もう一度興味・関心を持ってみませんか(その3)-対数はどこで役に立っているのか-」(2021.10.8)で紹介した。この「平均律」は(無理数による)等比数列に基づいているが、各音を表すのに指数表記が使用されることになる。
これに対して、古代ギリシャのピタゴラスが策定した2とされる「ピタゴラス音律」は、音階の全ての音と音程を周波数比が3:2の純正な完全五度3に基づいて導出する。周波数を、基準音から3/2倍(これは弦の長さを2/3倍にすることに相当)にし、2倍を超えたら半分にする(1オクターヴ下げる)ということを繰り返して、音階を作成する4。「ピタゴラス音律」は、初期ルネサンスまでの西洋音楽の標準的な音律であり、また中国や日本の伝統音楽の音律も同様の原理に基づく「三分損益法」と呼ばれる方法に基づいている。「ピタゴラス音律」も(3/2等の有理数の)等比数列に基づいているが、各音を表すのには分数表記が使用されることになる。
一方で、「純正律」は、周波数の比が単純な整数比である純正音程のみを用いて規定される音律で、各音の関係は分数で表される形になる。
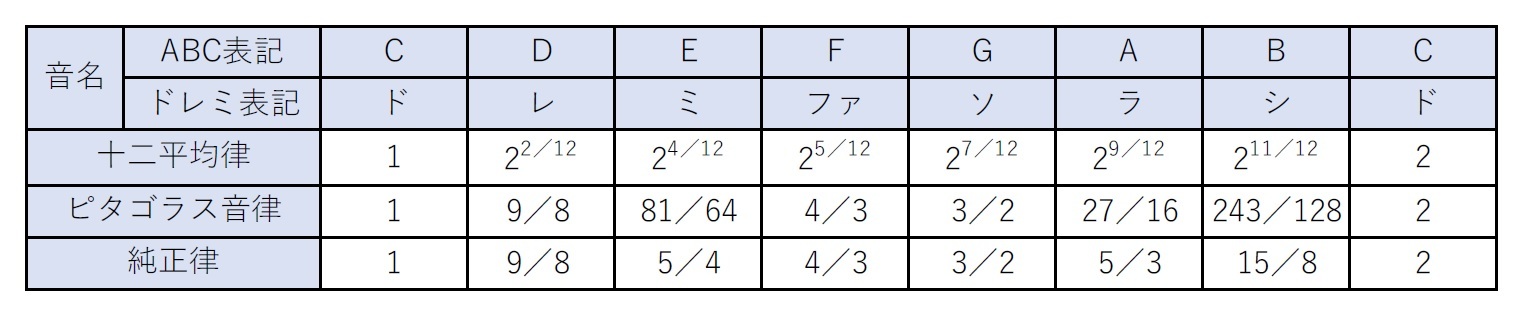
これら3つの音律によるドレミファソラシドの周波数は、以下の図表の通りとなる。
この図表における「ピタゴラス音律」の周波数については、以下のように設定される。
C: 1(基準音)
G: 3/2(Cの完全五度上)
D: 3/2×3/2×1/2= 9/8(Gの完全五度上の1オクターヴ下)
A: 9/8×3/2= 27/16(Dの完全五度上)
E: 27/16×3/2×1/2=81/64(Aの完全五度上の1オクターヴ下)
B: 81/64×3/2= 243/128(Eの完全五度上)
ここで、Fについては、Fの完全五度上がCとなるように設定され、
F:2÷3/2=4/3
となる。因みに、上記と同じ設定手法に従って得られる音は、F#と表される。
F#:243/128×3/2×1/2=729/512(Bの完全五度上の1オクターヴ下)
このうちの「平均律」は、1オクターヴなどの音程を均等な周波数比で分割した音律で、現在の西洋音楽で使用されている「十二平均律」は、隣り合う音(半音)の周波数比が常に
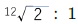 となる。
となる。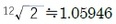 なので、音が一つ高くなると、周波数は約1.06倍になることになる1。これについては、以前の研究員の眼「「対数」に、もう一度興味・関心を持ってみませんか(その3)-対数はどこで役に立っているのか-」(2021.10.8)で紹介した。この「平均律」は(無理数による)等比数列に基づいているが、各音を表すのに指数表記が使用されることになる。
なので、音が一つ高くなると、周波数は約1.06倍になることになる1。これについては、以前の研究員の眼「「対数」に、もう一度興味・関心を持ってみませんか(その3)-対数はどこで役に立っているのか-」(2021.10.8)で紹介した。この「平均律」は(無理数による)等比数列に基づいているが、各音を表すのに指数表記が使用されることになる。これに対して、古代ギリシャのピタゴラスが策定した2とされる「ピタゴラス音律」は、音階の全ての音と音程を周波数比が3:2の純正な完全五度3に基づいて導出する。周波数を、基準音から3/2倍(これは弦の長さを2/3倍にすることに相当)にし、2倍を超えたら半分にする(1オクターヴ下げる)ということを繰り返して、音階を作成する4。「ピタゴラス音律」は、初期ルネサンスまでの西洋音楽の標準的な音律であり、また中国や日本の伝統音楽の音律も同様の原理に基づく「三分損益法」と呼ばれる方法に基づいている。「ピタゴラス音律」も(3/2等の有理数の)等比数列に基づいているが、各音を表すのには分数表記が使用されることになる。
一方で、「純正律」は、周波数の比が単純な整数比である純正音程のみを用いて規定される音律で、各音の関係は分数で表される形になる。
これら3つの音律によるドレミファソラシドの周波数は、以下の図表の通りとなる。
この図表における「ピタゴラス音律」の周波数については、以下のように設定される。
C: 1(基準音)
G: 3/2(Cの完全五度上)
D: 3/2×3/2×1/2= 9/8(Gの完全五度上の1オクターヴ下)
A: 9/8×3/2= 27/16(Dの完全五度上)
E: 27/16×3/2×1/2=81/64(Aの完全五度上の1オクターヴ下)
B: 81/64×3/2= 243/128(Eの完全五度上)
ここで、Fについては、Fの完全五度上がCとなるように設定され、
F:2÷3/2=4/3
となる。因みに、上記と同じ設定手法に従って得られる音は、F#と表される。
F#:243/128×3/2×1/2=729/512(Bの完全五度上の1オクターヴ下)
ところで、複数の音を同時にならす「和音」については、それぞれの音の周波数が簡単な整数比で表されるときに心地よく感じると言われている。一定の周波数をもった自然音は、その整数倍の周波数を持った倍音を成分として無限に含んでおり、こうした倍音の高さの音は、元の音(基音)の一部でもあるため同時に鳴らすと協和して聞こえるのがその理由のようである。因みに、最も有名な和音「ド、ミ、ソ」については、3つの音の周波数比は、1:1.260:1.498≒4:5:6 となっている。
「ピタゴラス音律」は、簡単な整数比で表される2音が良く響和するとの考えから、3:2の周波数比の繰り返しで策定されたが、これをより簡単な整数比で表現するような形で「純正律」が現れた。ただし、「純正律」では転調が難しくなる(周波数の比率がずれてしまい、元との音の関係が崩れてしまう)ことから、「十二平均律」が策定され、現在の主流となっている。ただし、これも完璧な音律というわけでもなく、今後、電子的に音を制御できるような楽器や演奏ができるようになれば、さらなる音律も普及してくるかもしれない。
1 欧州で最初に平均律を2の12乗根に基づいて算出したのは、以前の研究員の眼「小数について(その1)-小数の起源や記法等はどうなっているのか-」(2023.1.23)において、欧州で初めて小数を提唱したと紹介したシモン・ステヴィン(1548-1620)で、その後メルセンヌ数で有名なマラン・メルセンヌ(1588-1648)がより高精度の十二平均律を作成したとされている。
2 ピタゴラスは、鍛冶屋で重さの異なるハンマーの音を聞いて、音律を定めたと言われている。
3 「五度」はドとソのように音が(それ自身を含めて)5つ離れていること、「完全」は、その2つの音を同時に響かせると美しく響和する音程、という意味を有している。
4 ただし、この方法によると、十二平均律では1オクターヴの差になる音との間に「ピタゴラスコンマ」と呼ばれる若干のずれが生じる(平均律は無理数の比、ピタゴラス音律は有理数の比で音を設定しているので、これは不可避)形になる。
「ピタゴラス音律」は、簡単な整数比で表される2音が良く響和するとの考えから、3:2の周波数比の繰り返しで策定されたが、これをより簡単な整数比で表現するような形で「純正律」が現れた。ただし、「純正律」では転調が難しくなる(周波数の比率がずれてしまい、元との音の関係が崩れてしまう)ことから、「十二平均律」が策定され、現在の主流となっている。ただし、これも完璧な音律というわけでもなく、今後、電子的に音を制御できるような楽器や演奏ができるようになれば、さらなる音律も普及してくるかもしれない。
1 欧州で最初に平均律を2の12乗根に基づいて算出したのは、以前の研究員の眼「小数について(その1)-小数の起源や記法等はどうなっているのか-」(2023.1.23)において、欧州で初めて小数を提唱したと紹介したシモン・ステヴィン(1548-1620)で、その後メルセンヌ数で有名なマラン・メルセンヌ(1588-1648)がより高精度の十二平均律を作成したとされている。
2 ピタゴラスは、鍛冶屋で重さの異なるハンマーの音を聞いて、音律を定めたと言われている。
3 「五度」はドとソのように音が(それ自身を含めて)5つ離れていること、「完全」は、その2つの音を同時に響かせると美しく響和する音程、という意味を有している。
4 ただし、この方法によると、十二平均律では1オクターヴの差になる音との間に「ピタゴラスコンマ」と呼ばれる若干のずれが生じる(平均律は無理数の比、ピタゴラス音律は有理数の比で音を設定しているので、これは不可避)形になる。
音楽における音符・拍子
音符は、西洋音楽の楽譜において、音を書き表すのに使われる符号であるが、これには、全音符、2分音符、4分音符、8分音符、16分音符等があり、分数で呼ばれる形になっている。「〇分音符」の〇には(倍全音符を含めて)2のべき乗数値が入る。全音符が基準で、例えば4分音符は全音符の4分の1の長さになる。
音楽の拍子が「3/4」拍子といった形で表記されるが、これは分母で示される音符が小節内にいくつあるかを示している(「3/4」は、小節内に四分音符が3つ含まれている)。分数を表しているわけではなく、あくまでも表記や呼び方として使用されている。
音楽の拍子が「3/4」拍子といった形で表記されるが、これは分母で示される音符が小節内にいくつあるかを示している(「3/4」は、小節内に四分音符が3つ含まれている)。分数を表しているわけではなく、あくまでも表記や呼び方として使用されている。
カメラのシャッタースピード
このうち、実際のシャッタースピードは、上記の1段ごとだけでなく、1/3段や1/2段ずつ変えられる。
金のカラット数
金は、アルファベットのKを用いた「カラット(karat)」6という単位で、純度が表示されている。
このカラットの計算方法は、24進法7で行われており、24カラットが純金を表し、24KあるいはK24と表される(実際には、99.9%以上の純度の金が24カラットということになっている)。
18カラットは、18/24(=75%)の金を含んでいる、即ち純度75%の金、ということになり、18KあるいはK18と表される(これも最低75%の金を含んでいるということになっているようだ)。
6 ダイヤモンドの重さを表す「カラット(carat)」とは異なるものなので、混同しないように注意が必要となる。
7 24進法が採用された理由については、必ずしも明確ではないようだが、例えば、かつて金の取引に使用されていた「イナゴ豆」が24個単位で取引されており、その何粒分の重さか、が基準になっていたから、と言われているようだ。また、「karat」や「carat」は、古代ギリシャ語で「イナゴ豆」を意味する「κερατιον(keration)」が語源になっていると言われている。
このカラットの計算方法は、24進法7で行われており、24カラットが純金を表し、24KあるいはK24と表される(実際には、99.9%以上の純度の金が24カラットということになっている)。
18カラットは、18/24(=75%)の金を含んでいる、即ち純度75%の金、ということになり、18KあるいはK18と表される(これも最低75%の金を含んでいるということになっているようだ)。
6 ダイヤモンドの重さを表す「カラット(carat)」とは異なるものなので、混同しないように注意が必要となる。
7 24進法が採用された理由については、必ずしも明確ではないようだが、例えば、かつて金の取引に使用されていた「イナゴ豆」が24個単位で取引されており、その何粒分の重さか、が基準になっていたから、と言われているようだ。また、「karat」や「carat」は、古代ギリシャ語で「イナゴ豆」を意味する「κερατιον(keration)」が語源になっていると言われている。
(2023年04月28日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
新着記事
-
2025年10月28日
試練の5年に踏み出す中国(前編)-「第15次五カ年計画」の5年間は、どのような5年か -
2025年10月28日
地域医療連携推進法人の現状と今後を考える-「連携以上、統合未満」で協力する形態、その将来像は? -
2025年10月28日
東宝の自己株式取得-公開買付による取得 -
2025年10月28日
今週のレポート・コラムまとめ【10/21-10/27発行分】 -
2025年10月27日
大学卒女性の働き方別生涯賃金の推計(令和6年調査より)-正社員で2人出産・育休・時短で2億円超
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【分数について(その4)-分数は日常生活や社会でどのように使われているのか-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
分数について(その4)-分数は日常生活や社会でどのように使われているのか-のレポート Topへ



















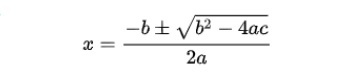


 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




