- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 「対数」に、もう一度興味・関心を持ってみませんか(その3)-対数はどこで役に立っているのか-
コラム
2021年10月08日
文字サイズ
- 小
- 中
- 大
はじめに
このシリーズの前回の研究員の眼「「対数」に、もう一度興味・関心を持ってみませんか(その2)-対数はどこで役に立っているのか-」(2021.9.27)では、対数が実際の社会の中で幅広く利用されている例として、「化石の年代測定」、「星の明るさ」、「地震の規模」及び「水素イオン指数」という身近な応用例について説明した。
今回の研究員の眼では、それ以外の応用例として、音の大きさ(dB(デシベル))、音のラウドネス(聴覚的な強さ)(phon(フォン))、音階や人間の感覚に関連する「ウェーバー-フェヒナーの法則(Weber–Fechner law)」等について説明することとしたい。
今回の研究員の眼では、それ以外の応用例として、音の大きさ(dB(デシベル))、音のラウドネス(聴覚的な強さ)(phon(フォン))、音階や人間の感覚に関連する「ウェーバー-フェヒナーの法則(Weber–Fechner law)」等について説明することとしたい。
音について
以前の研究員の眼「「三角関数」と「波」の関係-三角関数による「波」の表現と 各種の波(電磁波、音波、地震波等)-」(2021.5.18)で、音は疎密波であると述べたが、これは大気圧の圧力変動であるということができる。音の大きさや強さといった時に、一般の人にとって、それが何を指すのかは必ずしも明確ではない。ここでは、言葉の使い分けとして、「音の強さ」は音の物理的エネルギーを、「音の大きさ」は人の聴覚が感じる音の大きさ(ラウドネス)を表すものとする。
音の強さ
大気圧からの圧力変動である音の圧力の変動分を「音圧」と呼んで、音の物理的エネルギーの大きさを表している。この音圧の大きさを表現するのが、我々が良く耳にする「dB(デシベル)」である。
ご存知の方も多いと思われるが、一般的に圧力の単位としては「Pa(パスカル)」が使われ、1Paは1㎡に1N(ニュートン)=約0.1㎏の力が働いている状態を指している。天気予報でよく耳にする1気圧は1000hPa(ヘクトパスカル)=100000Paという巨大な圧力であるが、我々の周りに存在する音の音圧はこれに比べると圧倒的に小さいものとなっている。
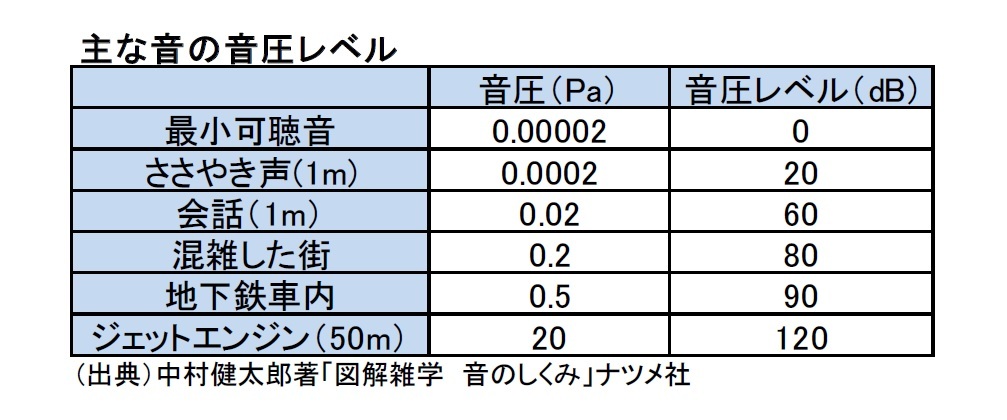
ただし、人間が聴くことができる音圧の範囲は非常に広く、6桁から7桁に及ぶとされている。例えば、人間が聴くことができる最小の音を「最小可聴音」というが、これは4kHz付近の周波数で0.00002Pa(20μPa)と言われている。また、ジェットエンジンの音を50m離れた場所で聞くとその音圧は20Pa程度と言われている。
そこで、音の強さを表現するのに、Paによる音圧ではなくて、「「最小可聴音」の音圧に対して何桁大きいかという値に20を掛けた数値」である「音圧レベル(sound pressure level:SPL)」を用いている。この時に使われる単位が「dB(デシベル)」ということになる。即ち音圧pに対して、音圧レベルLpは、p0(=0.00002Pa(20μPa))として、以下のように定義される。
Lp=20×log10(p/p0)
主な音の音圧レベルは、以下のようになっている。
ご存知の方も多いと思われるが、一般的に圧力の単位としては「Pa(パスカル)」が使われ、1Paは1㎡に1N(ニュートン)=約0.1㎏の力が働いている状態を指している。天気予報でよく耳にする1気圧は1000hPa(ヘクトパスカル)=100000Paという巨大な圧力であるが、我々の周りに存在する音の音圧はこれに比べると圧倒的に小さいものとなっている。
ただし、人間が聴くことができる音圧の範囲は非常に広く、6桁から7桁に及ぶとされている。例えば、人間が聴くことができる最小の音を「最小可聴音」というが、これは4kHz付近の周波数で0.00002Pa(20μPa)と言われている。また、ジェットエンジンの音を50m離れた場所で聞くとその音圧は20Pa程度と言われている。
そこで、音の強さを表現するのに、Paによる音圧ではなくて、「「最小可聴音」の音圧に対して何桁大きいかという値に20を掛けた数値」である「音圧レベル(sound pressure level:SPL)」を用いている。この時に使われる単位が「dB(デシベル)」ということになる。即ち音圧pに対して、音圧レベルLpは、p0(=0.00002Pa(20μPa))として、以下のように定義される。
Lp=20×log10(p/p0)
主な音の音圧レベルは、以下のようになっている。
音のラウドネス(聴覚的な強さ)
音の「ラウドネス(loudness)」というのは、人の聴覚が感じる音の大小を表す心理量である。これは心理量であるため、本来的には個々人が感じた「音量」を調査することでしか把握できない。音圧が倍になったからといって、音の大きさが2倍大きくなったと感じるわけではないが、一方で、ラウドネスは音圧と強い相関関係がある。従って、ラウドネスも、音圧を通じて、対数と強く関係していることになる。
そこで、ラウドネスを物理量から推定できる尺度として、「ラウドネスレベル(loudness level)」というものがある。これは、聴覚の特性に合わせて周波数補正され標準化された音圧レベルである。純音のラウドネスがその周波数によって変わる事実に基づいて、「等ラウドネス曲線」で補正をかけられた音圧レベルであり、単位は「フォン(phon)」(あるいはホン、ホーン)となる1。
「フォン (phon) 」は、基準音圧を20µPaとした音圧レベルのデシベル (dB) 値を周波数ごとに補正した値であり、以下の特徴を有している。
・1000Hzの純音に対しては音圧レベルのデシベル値に等しい。
・同じ音圧でも周波数によって聴覚的な聞こえ方が異なるので、同じデシベル値を示す音圧レベルでも周波数が違えば異なる値を示す。
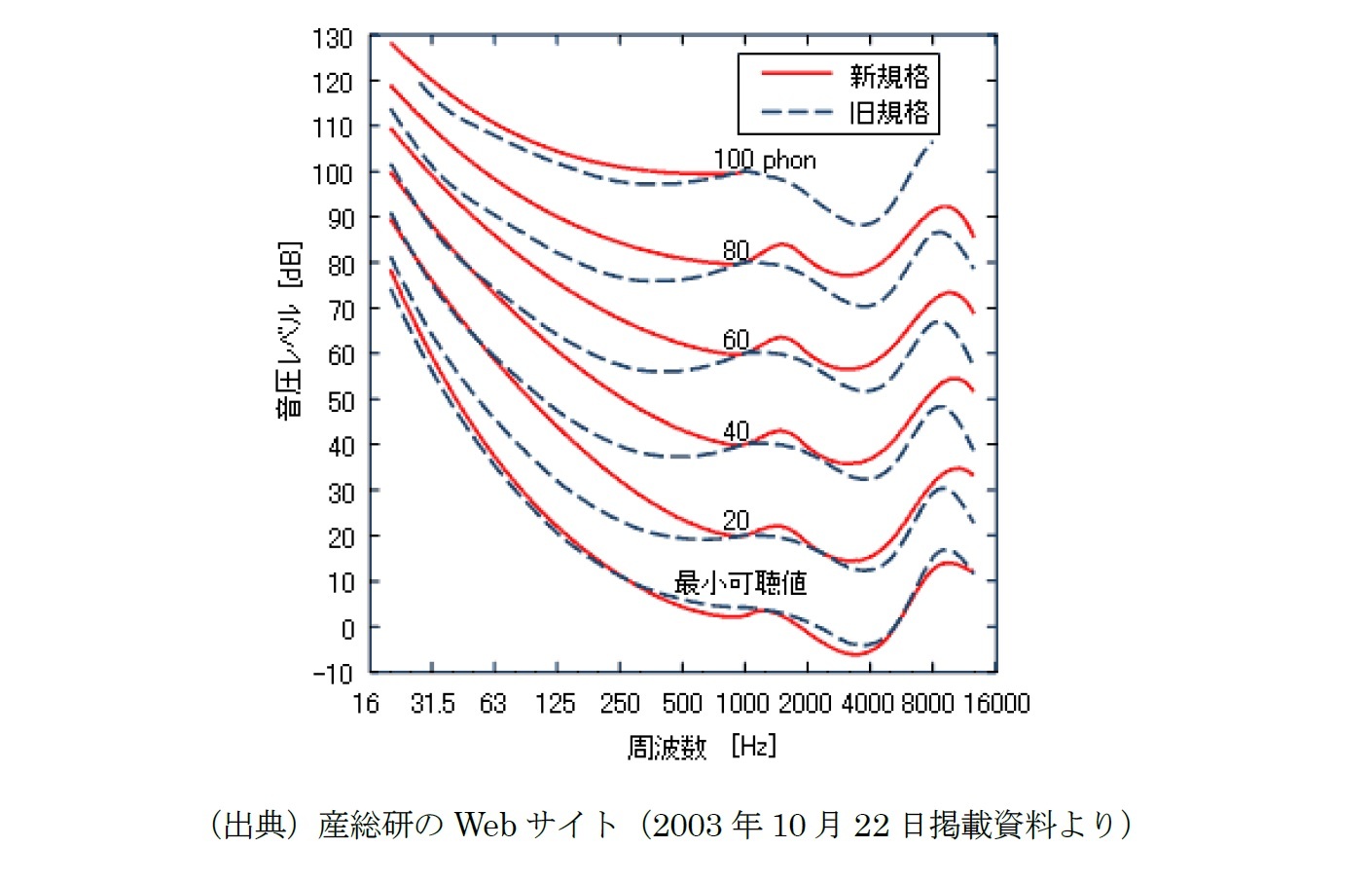
ラウドネスレベルを表すフォン(phon)と音圧レベルを表すデシベル (dB) との関係を示す「等ラウドネス曲線」は、以下の図表の通りになっている(産総研の資料に基づき、2003年にISO 226:2003 として改正された時の新旧を掲載したもの)。
この図表が示すように、同じ40dBという音圧レベルでも、1000Hzでは40フォンとなるが、100Hzならば10フォン程度、さらに50Hz以下になるとほとんど聞こえなくなってしまう。即ち、人の耳は、低周波数の感度が良くないことがわかる。人の可聴帯域の下限である20Hzの音が聞こえるためには70dB程度の音圧レベルが必要になってくる。一方で、かなり高い周波数に対しても感度が低下する。これに対して、3000~4000Hz付近の周波数の音の感度が良くなっている。また、音圧レベルの低い音は周波数による差がより大きいことがわかる。
そこで、ラウドネスを物理量から推定できる尺度として、「ラウドネスレベル(loudness level)」というものがある。これは、聴覚の特性に合わせて周波数補正され標準化された音圧レベルである。純音のラウドネスがその周波数によって変わる事実に基づいて、「等ラウドネス曲線」で補正をかけられた音圧レベルであり、単位は「フォン(phon)」(あるいはホン、ホーン)となる1。
「フォン (phon) 」は、基準音圧を20µPaとした音圧レベルのデシベル (dB) 値を周波数ごとに補正した値であり、以下の特徴を有している。
・1000Hzの純音に対しては音圧レベルのデシベル値に等しい。
・同じ音圧でも周波数によって聴覚的な聞こえ方が異なるので、同じデシベル値を示す音圧レベルでも周波数が違えば異なる値を示す。
ラウドネスレベルを表すフォン(phon)と音圧レベルを表すデシベル (dB) との関係を示す「等ラウドネス曲線」は、以下の図表の通りになっている(産総研の資料に基づき、2003年にISO 226:2003 として改正された時の新旧を掲載したもの)。
この図表が示すように、同じ40dBという音圧レベルでも、1000Hzでは40フォンとなるが、100Hzならば10フォン程度、さらに50Hz以下になるとほとんど聞こえなくなってしまう。即ち、人の耳は、低周波数の感度が良くないことがわかる。人の可聴帯域の下限である20Hzの音が聞こえるためには70dB程度の音圧レベルが必要になってくる。一方で、かなり高い周波数に対しても感度が低下する。これに対して、3000~4000Hz付近の周波数の音の感度が良くなっている。また、音圧レベルの低い音は周波数による差がより大きいことがわかる。
日本人が一般的な話をする時の周波数は、男性500Hz、女性800Hzと言われているが、赤ちゃんが大声で泣いた時の声の周波数は、2,000Hz以上の高周波音が含まれており、そのため赤ちゃんの泣き声は聞こえやすくなっていると言われている。
いずれにしても、この「等ラウドネス曲線」を用いることで、必要な音を聴き取りやすい周波数で流すことができ、また人の耳の特性に合わせた音響機器を設計することができるようになる。
1 「騒音レベル」を表すときにも「フォン」が使用されるが、これは「ラウドネスレベル」の「フョン」とは異なる定義を有している。「騒音レベル」は、周波数毎に定められた特性値を音圧レベルのdBに足して得られる。
いずれにしても、この「等ラウドネス曲線」を用いることで、必要な音を聴き取りやすい周波数で流すことができ、また人の耳の特性に合わせた音響機器を設計することができるようになる。
1 「騒音レベル」を表すときにも「フォン」が使用されるが、これは「ラウドネスレベル」の「フョン」とは異なる定義を有している。「騒音レベル」は、周波数毎に定められた特性値を音圧レベルのdBに足して得られる。
音階と平均律
「音階(scale)」というのは、音をその高さによって昇順あるいは降順にならべたものである。
「平均律(equal temperament)」は、1オクターブなどの音程を均等な周波数比で分割した音律(音高の相対的な関係の規定)のことをいい、一般には「十二平均律」を指すことが多い。
「十二平均律」は、1オクターブを12等分した音律である。音を1オクターブ高くすると、周波数は2倍になる(これが、オクターブの定義)となるので、十二平均律の隣り合う音(半音)の周波数比は常に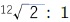 となる。
となる。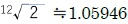 なので、音が一つ高くなると、周波数は約1.06倍になることになる。
なので、音が一つ高くなると、周波数は約1.06倍になることになる。
なお、複数の音を同時にならす「和音」については、それぞれの音の周波数が簡単な整数比で表されるときに心地よいと感じると言われている。一定の周波数をもった自然音は、その整数倍の周波数を持った倍音を成分として無限に含んでおり、こうした倍音の高さの音は、元の音(基音)の一部でもあるため同時に鳴らすと協和して聞こえるのがその理由のようである。因みに、最も有名な和音「ド、ミ、ソ」については、3つの音の周波数比が、1:1.260:1.498≒4:5:6 となっている。
「平均律(equal temperament)」は、1オクターブなどの音程を均等な周波数比で分割した音律(音高の相対的な関係の規定)のことをいい、一般には「十二平均律」を指すことが多い。
「十二平均律」は、1オクターブを12等分した音律である。音を1オクターブ高くすると、周波数は2倍になる(これが、オクターブの定義)となるので、十二平均律の隣り合う音(半音)の周波数比は常に
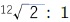 となる。
となる。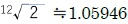 なので、音が一つ高くなると、周波数は約1.06倍になることになる。
なので、音が一つ高くなると、周波数は約1.06倍になることになる。なお、複数の音を同時にならす「和音」については、それぞれの音の周波数が簡単な整数比で表されるときに心地よいと感じると言われている。一定の周波数をもった自然音は、その整数倍の周波数を持った倍音を成分として無限に含んでおり、こうした倍音の高さの音は、元の音(基音)の一部でもあるため同時に鳴らすと協和して聞こえるのがその理由のようである。因みに、最も有名な和音「ド、ミ、ソ」については、3つの音の周波数比が、1:1.260:1.498≒4:5:6 となっている。
(参考)ギターの仕組みの概要2
ギターには6本の弦が張られていて、細い方の弦から、第1弦、第2弦、…第6弦と呼んでいる。ギターの弦をはじいて、振動させて得られる音の高さは、弦の太さや弦の張りつめ具合等によって変化し、弦が太くなるにつれて、音は低くなり、弦の貼りつめ度合いを高めると音は高くなる。音は、弦の長さによっても変化し、弦が短くなるにつれて、音は高くなる。このことは一般的な感覚として認識されているものと思われる。
1つの弦を考えた場合、ギターには「フレット」と呼ばれる部分があって、この部分を指で押さえることで、振動する弦の長さが変わり、出る音の高さが変わってくることになる。
実は、このフレットは、サウンドホールまでの弦の長さから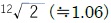 倍の刻みになるような位置に設定されている3。これにより、弦の振動する長さが1.06倍になるにつれて、出る音の高さが半音ずつ変化していくことになる。フレットは全部で20あるので、元の弦の長さは、サウンドホールに最も近いフレットを抑えた時と比べて、
倍の刻みになるような位置に設定されている3。これにより、弦の振動する長さが1.06倍になるにつれて、出る音の高さが半音ずつ変化していくことになる。フレットは全部で20あるので、元の弦の長さは、サウンドホールに最も近いフレットを抑えた時と比べて、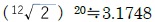 倍となり、即ち1つの弦で2オクターブ弱の範囲の音が出せる形になっている。
倍となり、即ち1つの弦で2オクターブ弱の範囲の音が出せる形になっている。
これを算式で示すと、以下の通りとなる。
ある弦の長さをa0とし、n番目のフレットを抑えた時の弦の長さをanとすると、

となっている。これはまた、(その「十二平均律」の定義から明らかだが)弦の長さが1/2になれば、音が1オクターブ高くなることを表している。これにより、

となって、弦の長さから、音の高さが求められることになり、対数が使用されていることがわかる。
今まで、ネックに並んでいるフレットの間隔が、ボディに近いほど狭くなっているのを疑問に感じていた方々もおられるかもしれないが、こうした理由によるものである。
なお、第1弦と第6弦では、出る音の高さが2オクターブ異なるようになっているので、結果的にギターは約4オクターブの音が出せるようになっているようだ。
2 ここの記述は、以下のヤマハのWebサイト「楽器解体全書」を参照させていただいた。
https://www.yamaha.com/ja/musical_instrument_guide/classical_guitar/
3 上記の「楽器解体全書」によれば、実際は、様々な要素が絡んでくるので、より複雑な計算式でフレットの位置を算出しているようである。
ギターには6本の弦が張られていて、細い方の弦から、第1弦、第2弦、…第6弦と呼んでいる。ギターの弦をはじいて、振動させて得られる音の高さは、弦の太さや弦の張りつめ具合等によって変化し、弦が太くなるにつれて、音は低くなり、弦の貼りつめ度合いを高めると音は高くなる。音は、弦の長さによっても変化し、弦が短くなるにつれて、音は高くなる。このことは一般的な感覚として認識されているものと思われる。
1つの弦を考えた場合、ギターには「フレット」と呼ばれる部分があって、この部分を指で押さえることで、振動する弦の長さが変わり、出る音の高さが変わってくることになる。
実は、このフレットは、サウンドホールまでの弦の長さから
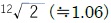 倍の刻みになるような位置に設定されている3。これにより、弦の振動する長さが1.06倍になるにつれて、出る音の高さが半音ずつ変化していくことになる。フレットは全部で20あるので、元の弦の長さは、サウンドホールに最も近いフレットを抑えた時と比べて、
倍の刻みになるような位置に設定されている3。これにより、弦の振動する長さが1.06倍になるにつれて、出る音の高さが半音ずつ変化していくことになる。フレットは全部で20あるので、元の弦の長さは、サウンドホールに最も近いフレットを抑えた時と比べて、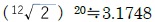 倍となり、即ち1つの弦で2オクターブ弱の範囲の音が出せる形になっている。
倍となり、即ち1つの弦で2オクターブ弱の範囲の音が出せる形になっている。これを算式で示すと、以下の通りとなる。
ある弦の長さをa0とし、n番目のフレットを抑えた時の弦の長さをanとすると、

となっている。これはまた、(その「十二平均律」の定義から明らかだが)弦の長さが1/2になれば、音が1オクターブ高くなることを表している。これにより、

となって、弦の長さから、音の高さが求められることになり、対数が使用されていることがわかる。
今まで、ネックに並んでいるフレットの間隔が、ボディに近いほど狭くなっているのを疑問に感じていた方々もおられるかもしれないが、こうした理由によるものである。
なお、第1弦と第6弦では、出る音の高さが2オクターブ異なるようになっているので、結果的にギターは約4オクターブの音が出せるようになっているようだ。
2 ここの記述は、以下のヤマハのWebサイト「楽器解体全書」を参照させていただいた。
https://www.yamaha.com/ja/musical_instrument_guide/classical_guitar/
3 上記の「楽器解体全書」によれば、実際は、様々な要素が絡んでくるので、より複雑な計算式でフレットの位置を算出しているようである。
ウェーバー-フェヒナーの法則
人間の感覚も「対数」的なものであると言われる。より具体的には、「人間の感覚の大きさは、受ける刺激の強さの対数に比例する」(あるいは「刺激による感覚の変化率は、現在の刺激量に反比例する」)というもので、これが「ウェーバー-フェヒナーの法則(Weber–Fechner law」4と呼ばれている。ドイツの生理学者エルンスト・ウェーバーが発見した法則を、その弟子であるグスタフ・フェヒナーが発展させた法則である。
これを算式で表すと、Rを刺激量、Eを感覚量とした場合に、感覚量の変化率は刺激量に反比例するので、
dE/dR = k/R (k は定数)
となる。これにより、
E=k logR +C
と表されることになる。
ウェーバーは、人が重さの変化を感じ取る実験をして、「100gの重さが110gになった時に初めて重さの変化を感じ取った人は、200gが210gになっても重さの変化を感じ取ることはなく、220gになって初めて重さの変化を感じ取る」という結果を得ている。
フェヒナーは、これを発展させ、「人間の感覚の大きさが、受ける刺激の強さの対数に比例する」ことを発見している。
4 ドイツ語名の日本語表記として「ヴェーバー-フェヒナーの法則」と呼ばれることもある。
これを算式で表すと、Rを刺激量、Eを感覚量とした場合に、感覚量の変化率は刺激量に反比例するので、
dE/dR = k/R (k は定数)
となる。これにより、
E=k logR +C
と表されることになる。
ウェーバーは、人が重さの変化を感じ取る実験をして、「100gの重さが110gになった時に初めて重さの変化を感じ取った人は、200gが210gになっても重さの変化を感じ取ることはなく、220gになって初めて重さの変化を感じ取る」という結果を得ている。
フェヒナーは、これを発展させ、「人間の感覚の大きさが、受ける刺激の強さの対数に比例する」ことを発見している。
4 ドイツ語名の日本語表記として「ヴェーバー-フェヒナーの法則」と呼ばれることもある。
ウェーバー-フェヒナーの法則の例
ウェーバー-フェヒナーの法則の例は、いくつか挙げられる。
ウェーバーが発見した重量感覚だけでなく、甘い辛いといった味覚(カレーライスの辛さの感じ方等)、臭いの強さに関する臭覚(臭気指数も対数で表され、臭いの成分量を半分にしても臭さはあまり変わらない等)、音の大きさに関する聴覚等の人間の五感は、この法則に支配されているようだ。
また、マネー感覚にも通じるところがある。投資等で、10万円が11万円に増えたら嬉しく思っても、100万円が101万円になってもあまり嬉しく感じないと思われる。逆に、1000円の商品が800円に値引きされていたら、安くなっていると感じるが、10000円の商品が9800円に値引きされていてもそれほど安くなったとは感じないものと思われる。
時間感覚でも同様で、待ち時間が予定の10分が実際に20分になったら、随分待たされたと感じるが、予定の1時間が実際には1時間10分になってもそれほど待たされたとは感じないと思われる。
実は、前回の研究員の眼で紹介した、星の明るさや地震の規模、さらには今回紹介した音の大きさ等も、人間の感覚に基づいているものが自然に感じられることから、その程度を表現する基準として、対数が使用されているといえる。
ウェーバーが発見した重量感覚だけでなく、甘い辛いといった味覚(カレーライスの辛さの感じ方等)、臭いの強さに関する臭覚(臭気指数も対数で表され、臭いの成分量を半分にしても臭さはあまり変わらない等)、音の大きさに関する聴覚等の人間の五感は、この法則に支配されているようだ。
また、マネー感覚にも通じるところがある。投資等で、10万円が11万円に増えたら嬉しく思っても、100万円が101万円になってもあまり嬉しく感じないと思われる。逆に、1000円の商品が800円に値引きされていたら、安くなっていると感じるが、10000円の商品が9800円に値引きされていてもそれほど安くなったとは感じないものと思われる。
時間感覚でも同様で、待ち時間が予定の10分が実際に20分になったら、随分待たされたと感じるが、予定の1時間が実際には1時間10分になってもそれほど待たされたとは感じないと思われる。
実は、前回の研究員の眼で紹介した、星の明るさや地震の規模、さらには今回紹介した音の大きさ等も、人間の感覚に基づいているものが自然に感じられることから、その程度を表現する基準として、対数が使用されているといえる。
まとめ
以上、今回の研究員の眼では、「対数」が応用されている例として、前回の研究員の眼で紹介した「化石の年代測定」、「星の明るさ」、「地震の規模」及び「水素イオン指数」という身近な例以外の応用例として、音の大きさ(dB(デシベル))、音のラウドネス(聴覚的な強さ)(phon(フォン))、音階について説明した。さらには、人間の感覚に関連する「ウェーバー-フェヒナーの法則(Weber–Fechner law)」についても説明し、前回の説明での身近な例における対数の使用がこの法則に関係していることを説明した。
今回簡単に紹介したもの以外にも、我々が意識していなくても、同様の感じ方をしている例は数多くあるものと思われる。何かの折に、この研究員の眼を思い出して、そういえばこれもウェーバー-フェヒナーの法則に従っているのだな、と感じていただければと思う。
また、人間の感覚が幅広く「対数」で支配されているということで、少しは「対数」に対する興味・関心を増大させていただけたら、と思っている。
今回簡単に紹介したもの以外にも、我々が意識していなくても、同様の感じ方をしている例は数多くあるものと思われる。何かの折に、この研究員の眼を思い出して、そういえばこれもウェーバー-フェヒナーの法則に従っているのだな、と感じていただければと思う。
また、人間の感覚が幅広く「対数」で支配されているということで、少しは「対数」に対する興味・関心を増大させていただけたら、と思っている。
(2021年10月08日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
新着記事
-
2025年10月28日
今週のレポート・コラムまとめ【10/21-10/27発行分】 -
2025年10月27日
秋の夜長に市民と経済の主食を考える-農業と電力はこれからも日本の食欲を満たせるのか -
2025年10月27日
大学卒女性の働き方別生涯賃金の推計(令和6年調査より)-正社員で2人出産・育休・時短で2億円超 -
2025年10月27日
なぜ味噌汁は動くのか -
2025年10月24日
米連邦政府閉鎖と代替指標の動向-代替指標は労働市場減速とインフレ継続を示唆、FRBは政府統計を欠く中で難しい判断を迫られる
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【「対数」に、もう一度興味・関心を持ってみませんか(その3)-対数はどこで役に立っているのか-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
「対数」に、もう一度興味・関心を持ってみませんか(その3)-対数はどこで役に立っているのか-のレポート Topへ



















 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




