- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 「対数」に、もう一度興味・関心を持ってみませんか(その2)-対数はどこで役に立っているのか-
コラム
2021年09月27日
文字サイズ
- 小
- 中
- 大
はじめに
以前の研究員の眼「「対数」に、もう一度興味・関心を持ってみませんか(その1)-対数って、何だろう?」(2021.6.4)では、対数の概念について、その語源や定義、さらには基本公式やグラフについて説明した。その「まとめ」において、対数は実際の社会の中で幅広く利用されているとして、いくつかの例を挙げておいた。
今回の研究員の眼では、そのうちの「化石の年代測定」、「星の明るさ」、「地震の規模」及び「水素イオン指数」という身近な応用例について説明することとしたい。
今回の研究員の眼では、そのうちの「化石の年代測定」、「星の明るさ」、「地震の規模」及び「水素イオン指数」という身近な応用例について説明することとしたい。
化石の年代測定
「化石の年代測定」というのは、おそらく対数が使用されている例として、最も有名なのではないかと思われる。これは、放射性元素の減少量に基づいて、年代測定を行うものである。
放射性物質に含まれる原子核は不安定で、放射線を出して「崩壊」して、他の原子核に変化していくが、その確率は放射性物質の種類ごとに一定の値となっている。多数の放射性物質の原子が「崩壊」を起こして元の個数の1/2になる時間を「半減期」というが、この「半減期」も放射性物質ごとに決まっている。
このことを利用して、生物の遺骸に含まれている特定の放射性物質の量を測定することができれば、その生物が死んでからどれくらいの年月が経過したのかを知ることができることになる。
「放射性炭素年代測定(radiocarbon dating)」は、「炭素14(14C)」と呼ばれる放射性物質を利用する手法である。炭素14は大気上層で太陽から来る宇宙線によって絶えず窒素からつくられているため、地球の自然の生物圏内では炭素14の存在比率がほぼ一定となっている。生物の内部における存在比率も、死ぬまで変わらないが、死後は新しい炭素の補給が止まることから、存在比率が下がっていくことになる。この性質と炭素14の半減期が5730年であることを利用して年代測定を行うことができる。
具体的には、例えば、ある生物の化石の炭素14の量が5分の1に減少していたとする。
炭素14の半減期が5730年であることから、毎年の減少率をpとすれば、
p5730=1/2
となっている。これにより、
p=(1/2)1/5730
一方で、5分の1に減少する年数をxとすると、
px=1/5
従って、
(1/2)x/5730=1/5
(x/5730)log10(1/2)= log10(1/5)
x=5730×log105/log102=5730×0.69897/0.30103=13305
となり、この化石は約13305年前のものということになる。
放射性物質に含まれる原子核は不安定で、放射線を出して「崩壊」して、他の原子核に変化していくが、その確率は放射性物質の種類ごとに一定の値となっている。多数の放射性物質の原子が「崩壊」を起こして元の個数の1/2になる時間を「半減期」というが、この「半減期」も放射性物質ごとに決まっている。
このことを利用して、生物の遺骸に含まれている特定の放射性物質の量を測定することができれば、その生物が死んでからどれくらいの年月が経過したのかを知ることができることになる。
「放射性炭素年代測定(radiocarbon dating)」は、「炭素14(14C)」と呼ばれる放射性物質を利用する手法である。炭素14は大気上層で太陽から来る宇宙線によって絶えず窒素からつくられているため、地球の自然の生物圏内では炭素14の存在比率がほぼ一定となっている。生物の内部における存在比率も、死ぬまで変わらないが、死後は新しい炭素の補給が止まることから、存在比率が下がっていくことになる。この性質と炭素14の半減期が5730年であることを利用して年代測定を行うことができる。
具体的には、例えば、ある生物の化石の炭素14の量が5分の1に減少していたとする。
炭素14の半減期が5730年であることから、毎年の減少率をpとすれば、
p5730=1/2
となっている。これにより、
p=(1/2)1/5730
一方で、5分の1に減少する年数をxとすると、
px=1/5
従って、
(1/2)x/5730=1/5
(x/5730)log10(1/2)= log10(1/5)
x=5730×log105/log102=5730×0.69897/0.30103=13305
となり、この化石は約13305年前のものということになる。
星の明るさ
星の明るさについては、「1等星」や「2等星」といった形で言い表されることは多くの方がご存知だと思う。こうした分類は、もともと紀元前150年頃、ギリシャの天文学者ヒッパルコス(Hipparchus)が始めたもので、夜空でもっとも明るい星を1等星、次に明るい星を2等星、そして眼で見える最も暗い星を6等星と名付けていた。
これが、現在は星の明るさがより精密に測定され、対数に基づいて定められる「等級(magnitude)」から分類されるものとなっている。以下で説明するように、等級の数値が小さいほど明るい星ということになる。星の明るさは、当然のことながら、「1」とか「2」とか言った不連続にしか存在するものではなく、無数に星があれば、その明るさはほぼ連続的に存在していることになる。従って、現在の等級の考え方に基づくと、例えば、「2等星」というのは、「等級が1.5以上2.5未満の範囲にある星」のことを指すと定義されることになる。
なお、等級は1未満、さらにはマイナスになることもある。さらには、もちろん6を超える等級もあり、例えば(我々には実眼では見ることができないが)「13等星」等と分類される星もある。例えば現在1等星として知られる星は21個あるが、「〇等星」の丸の数字が大きくなればなるほど該当する星の数は大きく増加していく構成になっている。
いずれにしても、ある星の「等級」がどうなるのか、あるいはどの「等星」に分類されるのかは、等級の定義において、起点となる原点の「0等級」をどう定義するのかによってくる。実は、等級にはいくつかの種類があり、また等級の原点にも主として2種類ある。
例えば、我々が通常、星図や星座早見盤などでみる等級は、地球から観測して得られる見かけ上の明るさによるもので「見かけの等級(apparent magnitude)」と呼ばれるものである。なお、これとは異なる概念で定義されるものとして、ヒトの肉眼による観測で得られる見かけの等級としての「実視等級(visual magnitude)」や、肉眼よりも近紫外線から青にかけての感度が高い写真の撮像から判定された等級としての「写真等級(photographic magnitude)」というものがある。いずれにしても、天体の明るさは距離の2乗に反比例することから、これらの等級は天体までの距離に依存することになる。
これに対して、天体を地球から10パーセク(pc)(1パーセクは、約 3.085677581×1016 m(約3.26光年)であることから、約32.6光年)の距離に置いたものと仮定したときの見かけの明るさで示された等級を「絶対等級(absolute magnitude)」と呼び、天体の絶対的な明るさの指標となっている。
その他にも等級の種類があるが、いずれの等級においても、等級間の関係については、「等級が1上がると、星の明るさは約2.5倍」になる。具体的には、等級が5等級小さくなると、明るさが100倍になる、すなわち1等級の差が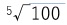 ≒ 2.512倍に相当するように定められる。則ち、等級をm、明るさをℓで表すと、2つの等級と明るさの間に以下の関係式が成り立つ。
≒ 2.512倍に相当するように定められる。則ち、等級をm、明るさをℓで表すと、2つの等級と明るさの間に以下の関係式が成り立つ。
m1-m2=-2.5log10(ℓ1/ℓ2)
これが、1856年に英国の天文学者ノーマン・ロバート・ポグソン(Norman Robert Pogson)が定義したもので、「ポグソンの式」と呼ばれて、定着している。これにより、等級の原点(ゼロ点)、即ち「0等級」の明るさℓ0を定めることで、等級は以下の式で定められることになる。
m=-2.5log10(ℓ1/ℓ0)
さて、それでは等級の原点(ゼロ点)、即ち「0等級」の明るさとはどう定義されているのだろうか。
これについても時代によって変遷があり、現在も「ベガ等級」と「AB等級」の2種類の等級の原点が主に使われている。これらの詳しい説明はここでは省略させていただくことにするが、いずれにしても両者は波長が548.0 nm のときに一致するというようなものである。
なお、地球からdパーセクの距離にある天体の見かけの等級 m と絶対等級 M の間には、その定義から
m-M= -2.5log10(102/d2)=5 log10d-5
という関係が成り立つことになる。「m-M」は「距離指数」と呼ばれ、ある天体の絶対等級を何らかの方法で見積もることができれば、距離指数を使うことでその天体までの距離を見積もることができることになる。
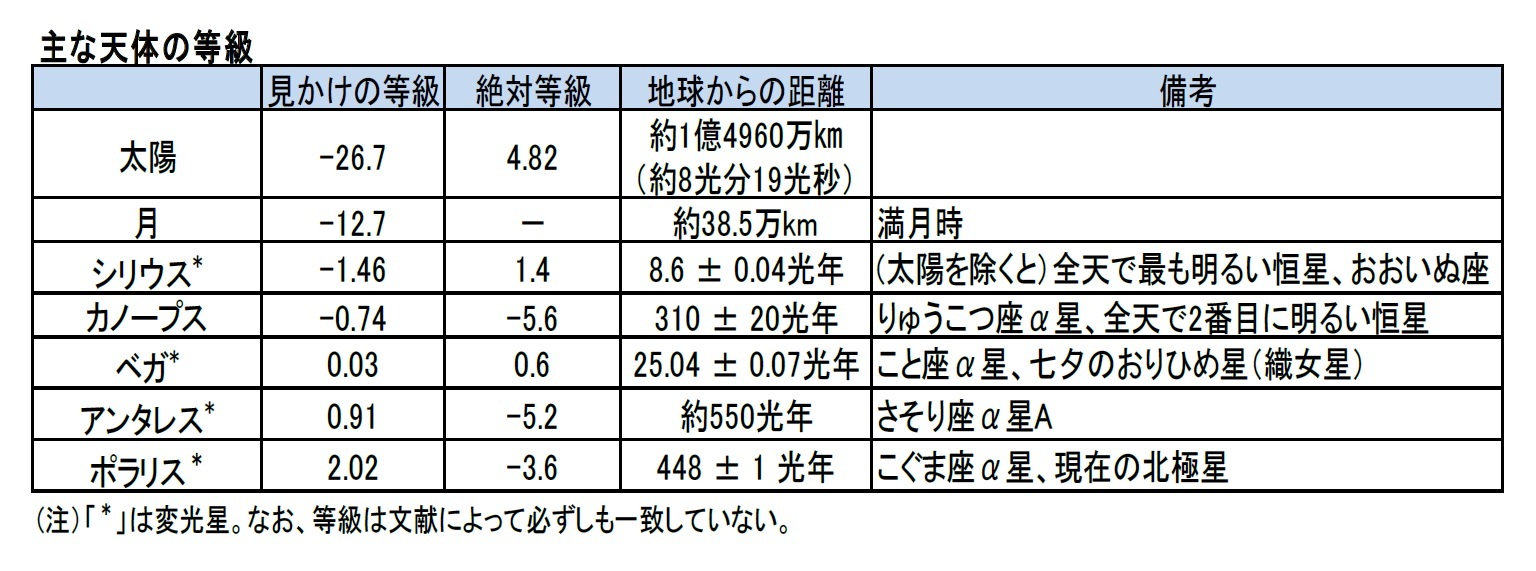
因みに、主な天体の等級等は以下の通りとなっている。惑星のように明るさが変わるものは、その時々の明るさが等級で示される。例えば、金星は、もっとも明るくなったときは、マイナス4.3等級まで明るくなるようだ。等級は文献によっても必ずしも一致していないようなので、あくまでもこの図表の数値は1つの参考程度にみていただければと思う。
これが、現在は星の明るさがより精密に測定され、対数に基づいて定められる「等級(magnitude)」から分類されるものとなっている。以下で説明するように、等級の数値が小さいほど明るい星ということになる。星の明るさは、当然のことながら、「1」とか「2」とか言った不連続にしか存在するものではなく、無数に星があれば、その明るさはほぼ連続的に存在していることになる。従って、現在の等級の考え方に基づくと、例えば、「2等星」というのは、「等級が1.5以上2.5未満の範囲にある星」のことを指すと定義されることになる。
なお、等級は1未満、さらにはマイナスになることもある。さらには、もちろん6を超える等級もあり、例えば(我々には実眼では見ることができないが)「13等星」等と分類される星もある。例えば現在1等星として知られる星は21個あるが、「〇等星」の丸の数字が大きくなればなるほど該当する星の数は大きく増加していく構成になっている。
いずれにしても、ある星の「等級」がどうなるのか、あるいはどの「等星」に分類されるのかは、等級の定義において、起点となる原点の「0等級」をどう定義するのかによってくる。実は、等級にはいくつかの種類があり、また等級の原点にも主として2種類ある。
例えば、我々が通常、星図や星座早見盤などでみる等級は、地球から観測して得られる見かけ上の明るさによるもので「見かけの等級(apparent magnitude)」と呼ばれるものである。なお、これとは異なる概念で定義されるものとして、ヒトの肉眼による観測で得られる見かけの等級としての「実視等級(visual magnitude)」や、肉眼よりも近紫外線から青にかけての感度が高い写真の撮像から判定された等級としての「写真等級(photographic magnitude)」というものがある。いずれにしても、天体の明るさは距離の2乗に反比例することから、これらの等級は天体までの距離に依存することになる。
これに対して、天体を地球から10パーセク(pc)(1パーセクは、約 3.085677581×1016 m(約3.26光年)であることから、約32.6光年)の距離に置いたものと仮定したときの見かけの明るさで示された等級を「絶対等級(absolute magnitude)」と呼び、天体の絶対的な明るさの指標となっている。
その他にも等級の種類があるが、いずれの等級においても、等級間の関係については、「等級が1上がると、星の明るさは約2.5倍」になる。具体的には、等級が5等級小さくなると、明るさが100倍になる、すなわち1等級の差が
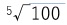 ≒ 2.512倍に相当するように定められる。則ち、等級をm、明るさをℓで表すと、2つの等級と明るさの間に以下の関係式が成り立つ。
≒ 2.512倍に相当するように定められる。則ち、等級をm、明るさをℓで表すと、2つの等級と明るさの間に以下の関係式が成り立つ。m1-m2=-2.5log10(ℓ1/ℓ2)
これが、1856年に英国の天文学者ノーマン・ロバート・ポグソン(Norman Robert Pogson)が定義したもので、「ポグソンの式」と呼ばれて、定着している。これにより、等級の原点(ゼロ点)、即ち「0等級」の明るさℓ0を定めることで、等級は以下の式で定められることになる。
m=-2.5log10(ℓ1/ℓ0)
さて、それでは等級の原点(ゼロ点)、即ち「0等級」の明るさとはどう定義されているのだろうか。
これについても時代によって変遷があり、現在も「ベガ等級」と「AB等級」の2種類の等級の原点が主に使われている。これらの詳しい説明はここでは省略させていただくことにするが、いずれにしても両者は波長が548.0 nm のときに一致するというようなものである。
なお、地球からdパーセクの距離にある天体の見かけの等級 m と絶対等級 M の間には、その定義から
m-M= -2.5log10(102/d2)=5 log10d-5
という関係が成り立つことになる。「m-M」は「距離指数」と呼ばれ、ある天体の絶対等級を何らかの方法で見積もることができれば、距離指数を使うことでその天体までの距離を見積もることができることになる。
因みに、主な天体の等級等は以下の通りとなっている。惑星のように明るさが変わるものは、その時々の明るさが等級で示される。例えば、金星は、もっとも明るくなったときは、マイナス4.3等級まで明るくなるようだ。等級は文献によっても必ずしも一致していないようなので、あくまでもこの図表の数値は1つの参考程度にみていただければと思う。
地震の規模
地震の強さを表す指標の1つに、地震が発するエネルギーの大きさを基準とする「マグニチュード(magnitude)」がある。もう一つの有名な指標である「震度」は揺れの大きさを示しているが、地震の規模(エネルギー)が大きくても、震源地から遠く離れていれば震度は小さくなり、地震の規模(エネルギー)が小さくても震源地から近ければ震度は大きくなる、という関係がある。
このマグニチュードは、米国の地震学者チャールズ・リヒター(Charles Richter)によって1935年に定義された。マグニチュードは地震のエネルギーを1000の平方根を底とした対数で表され、マグニチュードが1増えると地震のエネルギーは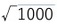 (=約31.6)倍に、マグニチュードが2増えると地震のエネルギーは1000倍となる。
(=約31.6)倍に、マグニチュードが2増えると地震のエネルギーは1000倍となる。
なお、リヒターの定義から、さらに改良が加えられた「モーメントマグニチュード」等の各種のマグニチュードが考案されてきている。
因みに、過去に大きな被害をもたらした主たる地震のマグニチュードは以下の通りとなっている。なお、広島の原爆が放出した全エネルギーはマグニチュードで言えば約5.5に相当するようである。
このマグニチュードは、米国の地震学者チャールズ・リヒター(Charles Richter)によって1935年に定義された。マグニチュードは地震のエネルギーを1000の平方根を底とした対数で表され、マグニチュードが1増えると地震のエネルギーは
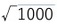 (=約31.6)倍に、マグニチュードが2増えると地震のエネルギーは1000倍となる。
(=約31.6)倍に、マグニチュードが2増えると地震のエネルギーは1000倍となる。なお、リヒターの定義から、さらに改良が加えられた「モーメントマグニチュード」等の各種のマグニチュードが考案されてきている。
因みに、過去に大きな被害をもたらした主たる地震のマグニチュードは以下の通りとなっている。なお、広島の原爆が放出した全エネルギーはマグニチュードで言えば約5.5に相当するようである。
水素イオン指数(酸性・アルカリ性の度合い)
「水素イオン指数」というのは、溶液の酸性・アルカリ性の度合いを表す物理量で、記号pH(ピーエッチ、ペーハー)で表されるものである。
水溶液の液性は、液体に含まれる水素イオン H+ と水酸化物イオン OH− の多寡で決まる。液体中に存在する H+ の数が OH− の数よりも多いとき、その水溶液は「酸性」となり、逆に、H+ の数が OH− の数よりも少ないとき、「アルカリ性」、H+ の数が OH− の数とちょうど同じときは、酸性でもアルカリ性でもなく、「中性」となる。
希薄溶液のpHは、「水素イオンの濃度をモル濃度で表した数値の逆数の常用対数」にほぼ等しくなる。則ち、[H+]で水素イオンのモル濃度を表すことにすると、以下の式で表される。
pH≒-log10[H+]
なお、分子6.023×1,023個分の質量が1molとなる。
純粋な水では、[H+]=[OH-]=10-7(mol/ℓ)となるので、pH=7となる。これらの積は[H+]×[OH-]=10-14 となり、これを「イオン積」という。この値は、温度が一定であれば、水溶液において一定に保たれる。則ち、水溶液の水素イオン濃度が10分の1になると、水酸化物イオンの濃度は10倍になり、逆に水素イオン濃度が10倍になると、水酸化物イオンの濃度は10分の1になる。
現在のpHは、水素イオンのモル濃度 [H+] ではなく、水素イオンの活量(実在溶液における実効モル濃度)aH+ に基づいて定義されている。
pH=-log10(aH+)
ただし、希薄水溶液に限れば、活量を使わずにモル濃度から求めた計算値が実測値とそれなりに一致している。
その定義により、pHに上限や下限があるわけではなく、例えばアルカリ乾電池の電解液のpHは14を超えている。
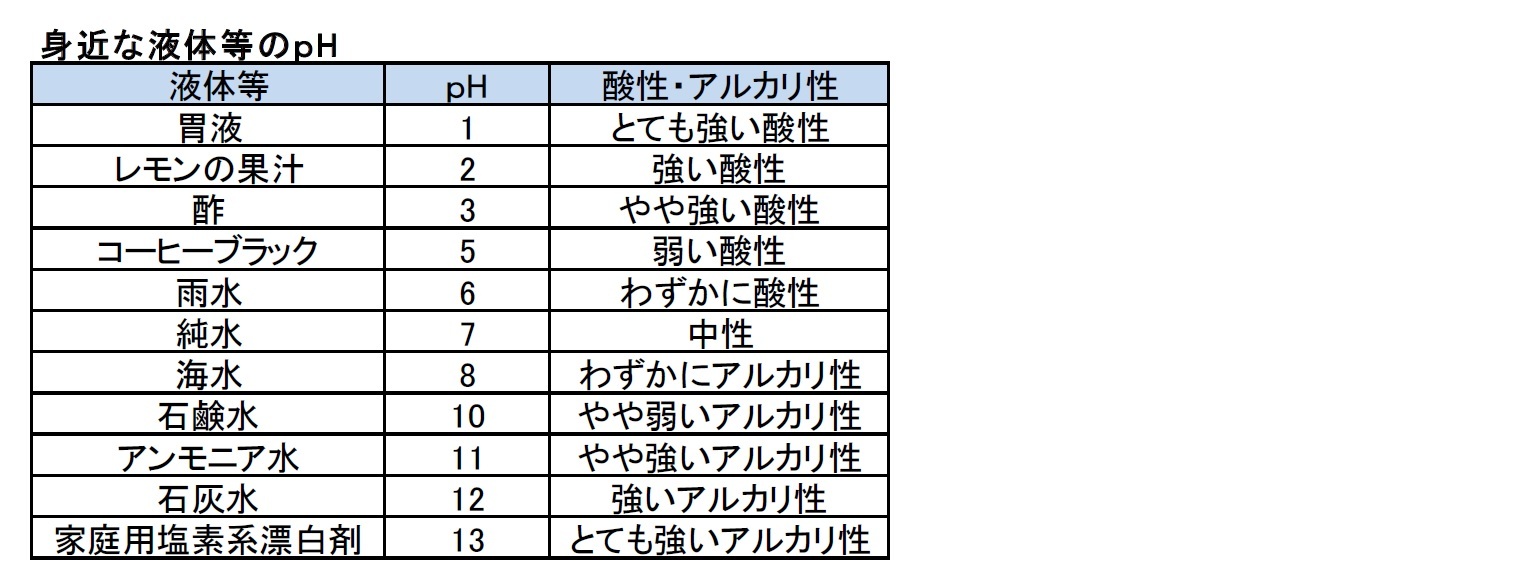
身近な液体等のpHは、以下の通りとなっている。
水溶液の液性は、液体に含まれる水素イオン H+ と水酸化物イオン OH− の多寡で決まる。液体中に存在する H+ の数が OH− の数よりも多いとき、その水溶液は「酸性」となり、逆に、H+ の数が OH− の数よりも少ないとき、「アルカリ性」、H+ の数が OH− の数とちょうど同じときは、酸性でもアルカリ性でもなく、「中性」となる。
希薄溶液のpHは、「水素イオンの濃度をモル濃度で表した数値の逆数の常用対数」にほぼ等しくなる。則ち、[H+]で水素イオンのモル濃度を表すことにすると、以下の式で表される。
pH≒-log10[H+]
なお、分子6.023×1,023個分の質量が1molとなる。
純粋な水では、[H+]=[OH-]=10-7(mol/ℓ)となるので、pH=7となる。これらの積は[H+]×[OH-]=10-14 となり、これを「イオン積」という。この値は、温度が一定であれば、水溶液において一定に保たれる。則ち、水溶液の水素イオン濃度が10分の1になると、水酸化物イオンの濃度は10倍になり、逆に水素イオン濃度が10倍になると、水酸化物イオンの濃度は10分の1になる。
現在のpHは、水素イオンのモル濃度 [H+] ではなく、水素イオンの活量(実在溶液における実効モル濃度)aH+ に基づいて定義されている。
pH=-log10(aH+)
ただし、希薄水溶液に限れば、活量を使わずにモル濃度から求めた計算値が実測値とそれなりに一致している。
その定義により、pHに上限や下限があるわけではなく、例えばアルカリ乾電池の電解液のpHは14を超えている。
身近な液体等のpHは、以下の通りとなっている。
雨水は、降水中に二酸化炭素が溶け込むことから、わずかに酸性となる。
人間の血液は、中性に近いがわずかにアルカリ性で、pH調節のための生理機能が働いていて、常に7.35から7.45の範囲に保たれている。
なお、学生時代に体験したように、リトマス紙で、水溶液の大まかな液性を調べることができる。青色のリトマス紙が赤色になれば酸性、赤色のリトマス紙が青色になればアルカリ性、そのいずれでもなければ中性いうことになる。ただし、リトマス紙では、pHの数値までは分からない。pH試験紙を用いると、pHの数値を知ることができる。
人間の血液は、中性に近いがわずかにアルカリ性で、pH調節のための生理機能が働いていて、常に7.35から7.45の範囲に保たれている。
なお、学生時代に体験したように、リトマス紙で、水溶液の大まかな液性を調べることができる。青色のリトマス紙が赤色になれば酸性、赤色のリトマス紙が青色になればアルカリ性、そのいずれでもなければ中性いうことになる。ただし、リトマス紙では、pHの数値までは分からない。pH試験紙を用いると、pHの数値を知ることができる。
まとめ
以上、今回の研究員の眼では、「対数」が応用されている例として、「化石の年代測定」、「星の明るさ」、「地震の規模」及び「水素イオン指数」という身近な応用例について説明した。
我々が身近に使用している「等級」や「マグニチュード」や「pH」といった基準や指標が実は対数を使用して定義されていることが認識いただけたのではないかと思う。
このシリーズの次回の研究員の眼では、今回紹介した以外の応用例として、音の大きさ(dB(デシベル))、音のラウドネス(聴覚的な強さ)(phon(フォン))、音階や人間の感覚に関連する「ウェーバー‐フェヒナーの法則(Weber–Fechner law)」等について説明することとしたい。
我々が身近に使用している「等級」や「マグニチュード」や「pH」といった基準や指標が実は対数を使用して定義されていることが認識いただけたのではないかと思う。
このシリーズの次回の研究員の眼では、今回紹介した以外の応用例として、音の大きさ(dB(デシベル))、音のラウドネス(聴覚的な強さ)(phon(フォン))、音階や人間の感覚に関連する「ウェーバー‐フェヒナーの法則(Weber–Fechner law)」等について説明することとしたい。
(2021年09月27日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
| 2025/09/25 | 数字の「49」に関わる各種の話題-49という数字に皆さんはどんなイメージを有しているのだろう- | 中村 亮一 | 研究員の眼 |
新着記事
-
2025年10月17日
EUの金融システムのリスクと脆弱性(2025秋)-欧州の3つの金融監督当局の合同委員会報告書 -
2025年10月17日
日本における「老衰死」増加の背景 -
2025年10月17日
選択と責任──消費社会の二重構造(1)-欲望について考える(2) -
2025年10月17日
首都圏の中古マンション価格~隣接する行政区単位での価格差は?~ -
2025年10月17日
「SDGs疲れ」のその先へ-2015年9月国連採択から10年、2030年に向け問われる「実装力」
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【「対数」に、もう一度興味・関心を持ってみませんか(その2)-対数はどこで役に立っているのか-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
「対数」に、もう一度興味・関心を持ってみませんか(その2)-対数はどこで役に立っているのか-のレポート Topへ




















 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




