- シンクタンクならニッセイ基礎研究所 >
- 「数学的帰納法」って何でしたっけ-「帰納法」と「演繹法」-
コラム
2021年08月06日
文字サイズ
- 小
- 中
- 大
はじめに
皆さん「数学的帰納法(きのうほう)」については、学生時代に学んだ覚えがあるのではないかと思われる。ただし、これに対する印象は、他の数学の概念に比べればわかりやすいと感じた方もおられるかもしれないが、これに関する試験問題に苦労して、やっぱり苦手意識を有しておられる方も多いのではないかと思われる。
今回は、この「数学的帰納法」に関する話題について述べてみたい。
今回は、この「数学的帰納法」に関する話題について述べてみたい。
「数学的帰納法」とは
「数学的帰納法(mathematical induction)」というのは、「自然数nに対する命題が、全ての自然数nについて成り立つことを証明せよ」というタイプの問題の証明において使用される手法の1つである。ここで、「命題」というのは、真偽が必ず定まる文章のことを言う。
具体的には、以下のような証明方法となる。
具体的には、以下のような証明方法となる。
ある命題Xについて
(1) n=1のときに、Xが成り立つ。
(2) n=kのときにXが成り立つとすると、n=k+1のときもXは成り立つ。
ことを証明することにより、
(3) (1)と(2)から、全ての自然数について、Xが成り立つ。
ことが示されることになる。
となり、n=k+1 のときにも上式が成り立つことが確認できる。
よって、全ての自然数nに対して、上式が成り立つことが証明された。
よって、全ての自然数nに対して、上式が成り立つことが証明された。
そもそもなぜ「数学的帰納法」と呼ぶのか-帰納法と演繹法
「数学的帰納法」という名称からは、それはより一般的な「帰納法」の一種ではないか、ということになる。そこで、まずは「帰納法」とそれに対峙する「演繹法(えんえきほう)」について簡単に説明する。
帰納法
「帰納法」とは、観察された事実やデータ等の具体的な事実から、一般的な法則を導き出す等、「特殊なケースから一般的な結論を推論する手法」である。いわゆる「経験則」に基づいた推論や「統計的手法」に基づいた結論の導出が「帰納法」の考え方を採用していることになる。
これは、多くの自然科学系の学問の基礎的な手法となっている。ただし、この形で得られた一般的な結論が必ずしも常に正しいとは限らない。特殊なケースが本当に全てのケースを代表しているとは限らないからである。
最も有名なケースとして挙げられるものが「カラス(烏)は全身が黒い」というものがある。
確かに我々が日常眼にするカラスは全て全身が黒い。従って、殆どの人がこれは正しいと思っている。ところが、世の中には「白黒2色」や「暗褐色に白斑」のカラスもいて、必ずしも全身が真っ黒のものだけではない。ただし、これは「カラス」というものの定義がどのようになってのかにもよると言えるかもしれない。動物分類学的には真っ黒ではないカラスもカラスなのかもしれないが、殆どの人にとって、真っ黒なものだけが(我々が通常認識している)カラスだと思っているから、何ら問題はないとの考え方もできるのかもしれない。
いずれにしても、「帰納法」は常にこうした要素を内在していることを認識しておく必要がある。
これは、多くの自然科学系の学問の基礎的な手法となっている。ただし、この形で得られた一般的な結論が必ずしも常に正しいとは限らない。特殊なケースが本当に全てのケースを代表しているとは限らないからである。
最も有名なケースとして挙げられるものが「カラス(烏)は全身が黒い」というものがある。
確かに我々が日常眼にするカラスは全て全身が黒い。従って、殆どの人がこれは正しいと思っている。ところが、世の中には「白黒2色」や「暗褐色に白斑」のカラスもいて、必ずしも全身が真っ黒のものだけではない。ただし、これは「カラス」というものの定義がどのようになってのかにもよると言えるかもしれない。動物分類学的には真っ黒ではないカラスもカラスなのかもしれないが、殆どの人にとって、真っ黒なものだけが(我々が通常認識している)カラスだと思っているから、何ら問題はないとの考え方もできるのかもしれない。
いずれにしても、「帰納法」は常にこうした要素を内在していることを認識しておく必要がある。
演繹法
こうした「帰納法」に対応する手法が「演繹法」と言われているものである。これは、「一般的な原理等から、特殊な結論を導き出す手法」である。その代表的な手法として「三段論法」が挙げられる。即ち、
この「演繹法」については、前提となっている一般的な原理が正しければ、結論も常に正しいことになる。
大前提:AはBである。
小前提:BはCである。
結論 :従って、AはCである。
この「演繹法」については、前提となっている一般的な原理が正しければ、結論も常に正しいことになる。
なぜ「数学的帰納法」と呼ばれるのか
数学における証明においては、一般的に「演繹法」が使用されている。
そうした中にあって、「数学的帰納法」については、限られた自然数の例から、次々と命題の正しさが証明されていき、一般的な結論を導き出していることから、それがいかにも「帰納的」に見えるということで「帰納法」という名称が付されている。
以前に「数学記号の由来」シリーズの研究員の眼の中で、例えば「∞(無限大)」の記号を導入したとして紹介したジョン・ウォリス(John Wallis)が初めてこの手法に「induction」の名称を使用したとされている。
ところが、「数学的帰納法」によって証明される結論は、その手法の使用に過ちがなければ常に正しいことになるし、その証明方法はまさに「演繹的」であるとの言い方ができるので、実は「演繹法」の一種ではないかとも言われている。
ところで、「数学的帰納法」を最初に使用したのは、17世紀の著名なフランスの数学者ブレーズ・パスカル(Blaise Pascal)で、彼が1654年に発表した「三角形に関する論文(Traite du Triangle Arithmetique)」においてであるとされている。数学の世界におけるもう一つの有名な証明法である「背理法」(帰謬法)については、紀元前300年頃に活躍したユークリッド(Euclid)が「素数が無数にある」ことの証明で使用していることと比較すると、相当に新しい手法であることがわかる。
以上ここまで、「帰納法」と「演繹法」について述べてきた。数学の世界の証明は、ある意味で全て「演繹的」であるといえるが、その証明すべき命題や仮説を導き出す際には経験則等に基づいた「帰納的」な考え方が採用されている。「演繹法」で使用されている原理等も、今は自明な命題や前提として認識されているかもしれないが、帰納的に導かれてきたものであるともいえる。その意味で、2つの手法は相互に関連しあって、ともに重要な位置付けを有するものとなっている。
そうした中にあって、「数学的帰納法」については、限られた自然数の例から、次々と命題の正しさが証明されていき、一般的な結論を導き出していることから、それがいかにも「帰納的」に見えるということで「帰納法」という名称が付されている。
以前に「数学記号の由来」シリーズの研究員の眼の中で、例えば「∞(無限大)」の記号を導入したとして紹介したジョン・ウォリス(John Wallis)が初めてこの手法に「induction」の名称を使用したとされている。
ところが、「数学的帰納法」によって証明される結論は、その手法の使用に過ちがなければ常に正しいことになるし、その証明方法はまさに「演繹的」であるとの言い方ができるので、実は「演繹法」の一種ではないかとも言われている。
ところで、「数学的帰納法」を最初に使用したのは、17世紀の著名なフランスの数学者ブレーズ・パスカル(Blaise Pascal)で、彼が1654年に発表した「三角形に関する論文(Traite du Triangle Arithmetique)」においてであるとされている。数学の世界におけるもう一つの有名な証明法である「背理法」(帰謬法)については、紀元前300年頃に活躍したユークリッド(Euclid)が「素数が無数にある」ことの証明で使用していることと比較すると、相当に新しい手法であることがわかる。
以上ここまで、「帰納法」と「演繹法」について述べてきた。数学の世界の証明は、ある意味で全て「演繹的」であるといえるが、その証明すべき命題や仮説を導き出す際には経験則等に基づいた「帰納的」な考え方が採用されている。「演繹法」で使用されている原理等も、今は自明な命題や前提として認識されているかもしれないが、帰納的に導かれてきたものであるともいえる。その意味で、2つの手法は相互に関連しあって、ともに重要な位置付けを有するものとなっている。
数学的帰納法のパターン
数学的帰納法とは言っても、いくつかの異なるパターンがある、以下にそのパターンとそれぞれの具体的な使用例を示しておく(なお、実際の証明については、ここでは省略している)。
1.基本パターン
まさに、1ページの四角囲みの中で説明しているパターンである。なお、ここでは、自然数の1からスタートしているが、1以外の任意の整数からスタートすることもできる。
1.基本パターン
まさに、1ページの四角囲みの中で説明しているパターンである。なお、ここでは、自然数の1からスタートしているが、1以外の任意の整数からスタートすることもできる。
2.直前だけでなく二つ前のケースも仮定するパターン
これは、基本パターンの(1)、(2)の代わりに、以下のような証明を行うパターンである。
「 aとbを自然数とする2次方程式x2-ax+b=0 の2つの実数解をα、βとするとき、
全ての自然数nについて、αn+βn は整数となる。 」
なお、このパターンでは、さらに3つ以上を仮定することもある。
また、偶数のケースと奇数のケースを分けて、それぞれのケースで、「n=kのときにXが成り立つとすると、n=k+2のときもXは成り立つ。」ことを示すことで、全ての自然数で成り立つことを証明するパターンもある。
これは、基本パターンの(1)、(2)の代わりに、以下のような証明を行うパターンである。
(1) n=1及びn=2ときに、Xが成り立つ。
(2) n=k及びn=k+1のときにXが成り立つとすると、n=k+2のときもXは成り立つ。
「 aとbを自然数とする2次方程式x2-ax+b=0 の2つの実数解をα、βとするとき、
全ての自然数nについて、αn+βn は整数となる。 」
なお、このパターンでは、さらに3つ以上を仮定することもある。
また、偶数のケースと奇数のケースを分けて、それぞれのケースで、「n=kのときにXが成り立つとすると、n=k+2のときもXは成り立つ。」ことを示すことで、全ての自然数で成り立つことを証明するパターンもある。
4.後ろ向き帰納法(無限降下法(infinite descent))
これは、これまでのパターンとは逆に、「n=kのときにXが成り立つとすると、n=k―1のときもXは成り立つ。」とするものである。実際には、以下のような証明パターンとなり、背理法と数学的帰納法を組み合わせた証明手法となっている。
例えば、このパターンは、フェルマーの最終定理として知られる 「xn+yn=zn(n≧3)となる自然数の解の組は存在しない」において、n=4のときの証明に使用される。さらには、「pが素数であるときに、√pが無理数になる」ことの証明にも使用される。
これは、これまでのパターンとは逆に、「n=kのときにXが成り立つとすると、n=k―1のときもXは成り立つ。」とするものである。実際には、以下のような証明パターンとなり、背理法と数学的帰納法を組み合わせた証明手法となっている。
命題Xが成り立たないような自然数nが存在すると仮定して、その最小値をkとしたときに、n=k-1でも成り立たないことを示すことで、これはkの取り方に矛盾することから、このようなkは存在しない。よって、全ての自然数nに対して命題Xが成り立つ。
17世紀の数学者ピエール・ド・フェルマー(Pierre de Fermat)によって始められたとされ、彼はこの証明法を好んで用いたと言われている。例えば、このパターンは、フェルマーの最終定理として知られる 「xn+yn=zn(n≧3)となる自然数の解の組は存在しない」において、n=4のときの証明に使用される。さらには、「pが素数であるときに、√pが無理数になる」ことの証明にも使用される。
6.多変数の数学的帰納法
これは、「複数の自然数のペア(m、n)全てに関して、命題が成り立つことを証明するために、原点から縦軸及び横軸にも成り立つことを証明していく」パターンである。
これは、「複数の自然数のペア(m、n)全てに関して、命題が成り立つことを証明するために、原点から縦軸及び横軸にも成り立つことを証明していく」パターンである。
数学的帰納法に関するパラドックス
「パラドックス(paradox)」とは、一見すると正しそうに見える前提と、妥当に見える推論から、受け入れがたい結論が得られる事を指す言葉である。数学的帰納法に関連しても、いくつかの有名なパラドックスが存在しているが、以下に1つだけ有名な具体例を挙げておく。
それは、「砂山のパラドックス」と呼ばれるもので、以下のようなものである。
これを奇妙に感じるのは、例えば「砂山」の定義が明確になっていないことが理由に挙げられる。即ち証明すべき命題が特定化されていない。これは、ある意味で先に述べた「カラス(烏)は全身が黒い」という命題にも通じている。数学的帰納法を使用する場合には、その証明すべき命題が明確に定義された適切なものでなければならないことになる。
このように、数学的帰納法を使用する場合には注意が必要である。そのこともあり、数学以外の世界ではあまり一般的に使用されていないようである。もちろん、繰り返しにはなるが、その根底にある「演繹的」な手法や「帰納的」な手法は、幅広く使用されている。
それは、「砂山のパラドックス」と呼ばれるもので、以下のようなものである。
砂山から砂を一粒減らしても、残りは砂山である。これを繰り返していけば、最後の砂一粒になってもそれは砂山である。
この種のパラドックスには、様々なバリエーションがあるが、いずれも「少量の変化では問題ないことから、数学的帰納法によりそれが累積した結果の大量の変化でも問題はない」という論理を展開している。これを奇妙に感じるのは、例えば「砂山」の定義が明確になっていないことが理由に挙げられる。即ち証明すべき命題が特定化されていない。これは、ある意味で先に述べた「カラス(烏)は全身が黒い」という命題にも通じている。数学的帰納法を使用する場合には、その証明すべき命題が明確に定義された適切なものでなければならないことになる。
このように、数学的帰納法を使用する場合には注意が必要である。そのこともあり、数学以外の世界ではあまり一般的に使用されていないようである。もちろん、繰り返しにはなるが、その根底にある「演繹的」な手法や「帰納的」な手法は、幅広く使用されている。
最後に
これまで「数学的帰納法」の考え方やその起源等、さらにはそれと関連する「演繹法」について述べてきた。「数学的帰納法」にもいろいろなパターンがあることを認識してもらうことで、今後何かの機会に利用できないかと考えてみていただければと思っている。
我々は、日常的に、明示的に意識してはいないが、常に、「帰納的」、「演繹的」な手法で物事を思考している。このことを再認識することで、今後各種の分析や判断等を行う機会において、このことを意識的に考えることで、適切な結論がより論理的に導き出せるようになるのではないかと思われる。
我々は、日常的に、明示的に意識してはいないが、常に、「帰納的」、「演繹的」な手法で物事を思考している。このことを再認識することで、今後各種の分析や判断等を行う機会において、このことを意識的に考えることで、適切な結論がより論理的に導き出せるようになるのではないかと思われる。
(2021年08月06日「研究員の眼」)
このレポートの関連カテゴリ
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/11/04 | 数字の「26」に関わる各種の話題-26という数字で思い浮かべる例は少ないと思われるが- | 中村 亮一 | 研究員の眼 |
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
新着記事
-
2025年11月07日
フィリピンGDP(25年7-9月期)~民間消費の鈍化で4.0%成長に減速、電子部品輸出は堅調 -
2025年11月07日
次回の利上げは一体いつか?~日銀金融政策を巡る材料点検 -
2025年11月07日
個人年金の改定についての技術的なアドバイス(欧州)-EIOPAから欧州委員会への回答 -
2025年11月07日
中国の貿易統計(25年10月)~輸出、輸入とも悪化。対米輸出は減少が続く -
2025年11月07日
英国金融政策(11月MPC公表)-2会合連続の据え置きで利下げペースは鈍化
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【「数学的帰納法」って何でしたっけ-「帰納法」と「演繹法」-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
「数学的帰納法」って何でしたっけ-「帰納法」と「演繹法」-のレポート Topへ




















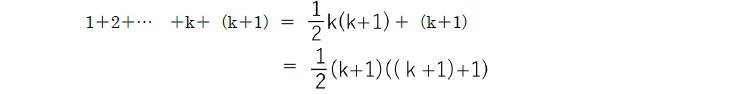



 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




