- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 分数について(その3)-既約分数に関する話題-
コラム
2023年04月25日
文字サイズ
- 小
- 中
- 大
はじめに
既約分数とファレイ数列
「規約分数(irreducible fraction)」というのは、分子と分母が1以外の公約数を持たない整数である分数、のことを指している。
「ファレイ数列(Farey sequence)」は、既約分数を順に並べた数列である。自然数nに対して、nに対応するファレイ数列Fn(あるいは次数nのファレイ数列Fn)とは、分母が n 以下で、 0 以上 1 以下の全ての既約分数を小さい順から並べてできる有限数列、を指している。 ただし、整数 0, 1 はそれぞれ分数 0/1、1/1として扱われる。ファレイ数列という名前は、イギリスの地質学者ジョン・ファレイ(John Farey Sr.)(1766-1826)に因んでいる1。
このファレイ数列Fnは、いくつかの興味深い性質を有している。
(1) その定義からFn+1で新たに現れる分数の分母はn+1となるが、これらは隣接することはない(これは、1≦k≦nに対して、k/(n+1)<k/n<(k+1)/(n+1) となることによる)
(2) 2つの分数 p/q、r/sが、あるファレイ数列で隣接している場合、この 2つの分数の間に新たな分数が加わるのは、次数 q + s のファレイ数列においてであり、それは p/q、r/sの中間数(mediant)と呼ばれる分数(p + r)/(q + s)となる。
不思議に思われるかもしれないが、こうして作成されていく中間数は、常に既約分数で、しかも全ての既約分数がちょうど1回だけ現れてくる。
(3) あるファレイ数列で、2 つの分数 p/q、r/sがこの順で隣接している場合、その差は
(qr – ps)/qs となるが、この時 にqr-ps = 1 となる。逆に、もし 0 ≦ p/q < r/s ≦ 1 であるような負でない整数 p, r と正の整数 q, s に対し、qr − ps = 1 が成り立つならば、p/q と r/s は、次数max {q, s} のファレイ数列において隣接している。
具体的に、nが1から8までのファレイ数列Fnは、以下の通りとなっているが、上記で説明した事実が確認できると思う。
「ファレイ数列(Farey sequence)」は、既約分数を順に並べた数列である。自然数nに対して、nに対応するファレイ数列Fn(あるいは次数nのファレイ数列Fn)とは、分母が n 以下で、 0 以上 1 以下の全ての既約分数を小さい順から並べてできる有限数列、を指している。 ただし、整数 0, 1 はそれぞれ分数 0/1、1/1として扱われる。ファレイ数列という名前は、イギリスの地質学者ジョン・ファレイ(John Farey Sr.)(1766-1826)に因んでいる1。
このファレイ数列Fnは、いくつかの興味深い性質を有している。
(1) その定義からFn+1で新たに現れる分数の分母はn+1となるが、これらは隣接することはない(これは、1≦k≦nに対して、k/(n+1)<k/n<(k+1)/(n+1) となることによる)
(2) 2つの分数 p/q、r/sが、あるファレイ数列で隣接している場合、この 2つの分数の間に新たな分数が加わるのは、次数 q + s のファレイ数列においてであり、それは p/q、r/sの中間数(mediant)と呼ばれる分数(p + r)/(q + s)となる。
不思議に思われるかもしれないが、こうして作成されていく中間数は、常に既約分数で、しかも全ての既約分数がちょうど1回だけ現れてくる。
(3) あるファレイ数列で、2 つの分数 p/q、r/sがこの順で隣接している場合、その差は
(qr – ps)/qs となるが、この時 にqr-ps = 1 となる。逆に、もし 0 ≦ p/q < r/s ≦ 1 であるような負でない整数 p, r と正の整数 q, s に対し、qr − ps = 1 が成り立つならば、p/q と r/s は、次数max {q, s} のファレイ数列において隣接している。
具体的に、nが1から8までのファレイ数列Fnは、以下の通りとなっているが、上記で説明した事実が確認できると思う。
1 ジョン・ファレイ Sr.(John Farey Sr.)(1766-1826)は、英国の地質学者で、これらの数列について、1816年に雑誌に論文を掲載したが、それ以前の1802年に、フランスの数学者シャルル・アロ(Charles Haros)が同様の結果を発表していた。また、ファレイは、ファレイ数列の各項が、隣接する数の中間数になると推測したが、その証明は与えておらず、それはフランスの数学者オーギュスタン=ルイ・コーシー(Augustin-Louis Cauchy)(1789-1857)によってなされている。
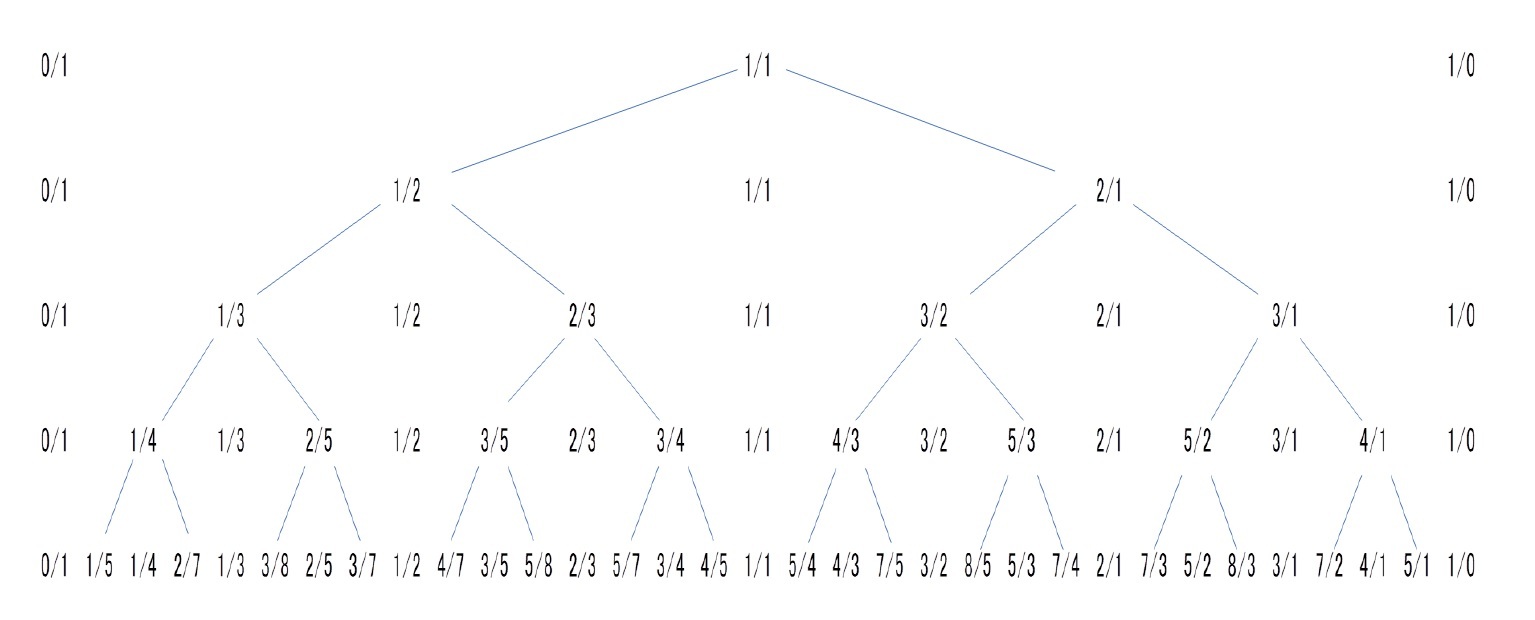
スターン=ブロコット木
範囲 (0,1) の有理数を含むスターン=ブロコット木の左側の部分木は、「ファレイ木(Farey Tree)」と呼ばれ、先に述べたファレイ数列(上図の場合、F1からF5及びF6からF8の一部)を作り出すものとなっている。
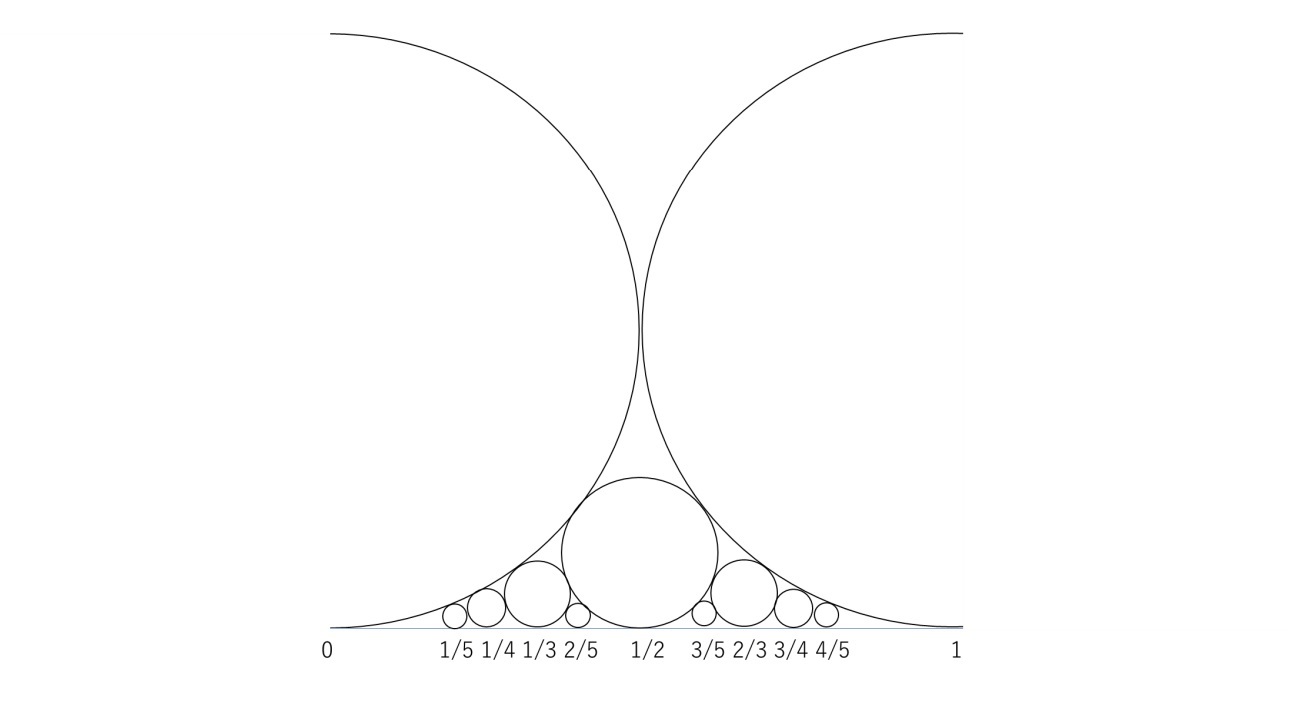
フォードの円
「フォードの円(Ford circle)」C(p/q)というのは、任意の既約分数p/qに対して、「中心が平面座標(p/q,1/2q2 )にある半径1/2q2の円」のことを指している。フォードの円の名称は、1938年にこれについて言及したアメリカの数学者Lester R. Ford(1886-1967)に由来している。
これらの円は全てx軸に接している。また、異なる2つの既約分数に対する2つのフォードの円は、互いに交わらないか接しているかのいずれかとなる(下図を参照)。
隣接する分数のフォードの円は接している。逆に、C(p/q)(0<p/q<1)に接するフォードの円は、ファレイ数列において隣接している分数のフォードの円になる。2つのフォードの円C(p/q)とC(r/s)は、|qr-ps|=1の場合にのみ接し、それ以外の場合には交わらない。
これらの円は全てx軸に接している。また、異なる2つの既約分数に対する2つのフォードの円は、互いに交わらないか接しているかのいずれかとなる(下図を参照)。
隣接する分数のフォードの円は接している。逆に、C(p/q)(0<p/q<1)に接するフォードの円は、ファレイ数列において隣接している分数のフォードの円になる。2つのフォードの円C(p/q)とC(r/s)は、|qr-ps|=1の場合にのみ接し、それ以外の場合には交わらない。
オイラー関数
具体的には、φ(n)の1から20までの値は、以下の通りとなる。
1, 1, 2, 2, 4, 2, 6, 4, 6, 4, 10, 4, 12, 6, 8, 8, 16, 6, 18, 8・・・
1, 1, 2, 2, 4, 2, 6, 4, 6, 4, 10, 4, 12, 6, 8, 8, 16, 6, 18, 8・・・
が成り立つ。ここで、d | n は d が n を割り切ることを意味しており、上記式は、全ての自然数は、その約数のオイラー関数の合計値に等しくなる、ことを表している。
具体的には、以下のような具合である。
φ(20)=φ(1)+φ(2)+φ(4)+φ(5)+φ(10)+φ(20)
=1+1+2+4+4+8
=20
具体的には、以下のような具合である。
φ(20)=φ(1)+φ(2)+φ(4)+φ(5)+φ(10)+φ(20)
=1+1+2+4+4+8
=20
フォードの円とオイラー関数
具体的にはこの値は0.87程度となる。
ファレイ数列と連分数展開の関係
となる。
2 下記の連分数展開の表記法については、前回の研究員の眼「分数について(その2)-連分数に関する話題-」(2023.4.18)を参照していただきたい。
2 下記の連分数展開の表記法については、前回の研究員の眼「分数について(その2)-連分数に関する話題-」(2023.4.18)を参照していただきたい。
その他の話題
最後になってしまったが、実は基本的で重要な話を述べておく。
任意の有理数は分母が正の既約分数として一意に表現される。これは素因数分解の一意性から証明される。
この事実は、√2等が無理数であることの証明に使用される。
任意の有理数は分母が正の既約分数として一意に表現される。これは素因数分解の一意性から証明される。
この事実は、√2等が無理数であることの証明に使用される。
最後に
今回は、分数を巡る話題のうち、既約分数に関する話題について、述べてきた。
ファレイ数列は、無理数の有理数近似を見つけるのに非常に便利なツールであり、各種の研究における計算の複雑さや最適性を特徴付ける上において利用され、洗練された効率的な計算方法を提供している。
いずれにしても、今回の内容は、知られている事実を述べることが中心で、その証明等については触れていない。それでも、小中学校で学んだ既約分数という概念だけを取り上げても、結構興味深い話題があることを知っていただいて、関心を抱いていただければと思って紹介することにした。
次回は、分数が日常生活や社会でどのように使われているのかについて、述べることとする。
ファレイ数列は、無理数の有理数近似を見つけるのに非常に便利なツールであり、各種の研究における計算の複雑さや最適性を特徴付ける上において利用され、洗練された効率的な計算方法を提供している。
いずれにしても、今回の内容は、知られている事実を述べることが中心で、その証明等については触れていない。それでも、小中学校で学んだ既約分数という概念だけを取り上げても、結構興味深い話題があることを知っていただいて、関心を抱いていただければと思って紹介することにした。
次回は、分数が日常生活や社会でどのように使われているのかについて、述べることとする。
(2023年04月25日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
新着記事
-
2025年10月28日
今週のレポート・コラムまとめ【10/21-10/27発行分】 -
2025年10月27日
秋の夜長に市民と経済の主食を考える-農業と電力はこれからも日本の食欲を満たせるのか -
2025年10月27日
大学卒女性の働き方別生涯賃金の推計(令和6年調査より)-正社員で2人出産・育休・時短で2億円超 -
2025年10月27日
なぜ味噌汁は動くのか -
2025年10月24日
米連邦政府閉鎖と代替指標の動向-代替指標は労働市場減速とインフレ継続を示唆、FRBは政府統計を欠く中で難しい判断を迫られる
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【分数について(その3)-既約分数に関する話題-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
分数について(その3)-既約分数に関する話題-のレポート Topへ





















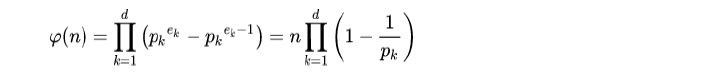



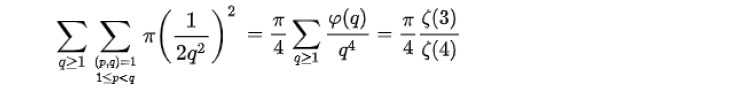




 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




