5回連続成功までに何回かかる?－練習が “地獄の猛特訓” に変貌するとき

保険研究部主席研究員兼気候変動リサーチセンターチーフ気候変動アナリスト兼ヘルスケアリサーチセンター主席研究員篠原拓也

このレポートの関連カテゴリ

◇ 野球の守備練習－「5回連続でエラーをしなかったら終了」の場合、平均して、何本ノックを受ける?

さて、話をコイン投げから、基本動作の繰り返し練習に戻そう。野球の守備練習でノックを受ける場合を考えてみる。ある野球チームの練習方法は、「5回連続でエラーをしなかったら終了」として、それまでノックを受け続けるものとしよう。さて、このチームの選手は、平均して、何回ノックを受ける必要があるだろうか?

守備が上手い選手と下手な選手がいるだろうから、一概には言えない。そこで、ある選手が1回のノックでエラーをしない確率をp、エラーをする確率を (1-p) (pは、0～1の値) として、この選手の平均ノック回数を考えてみる。

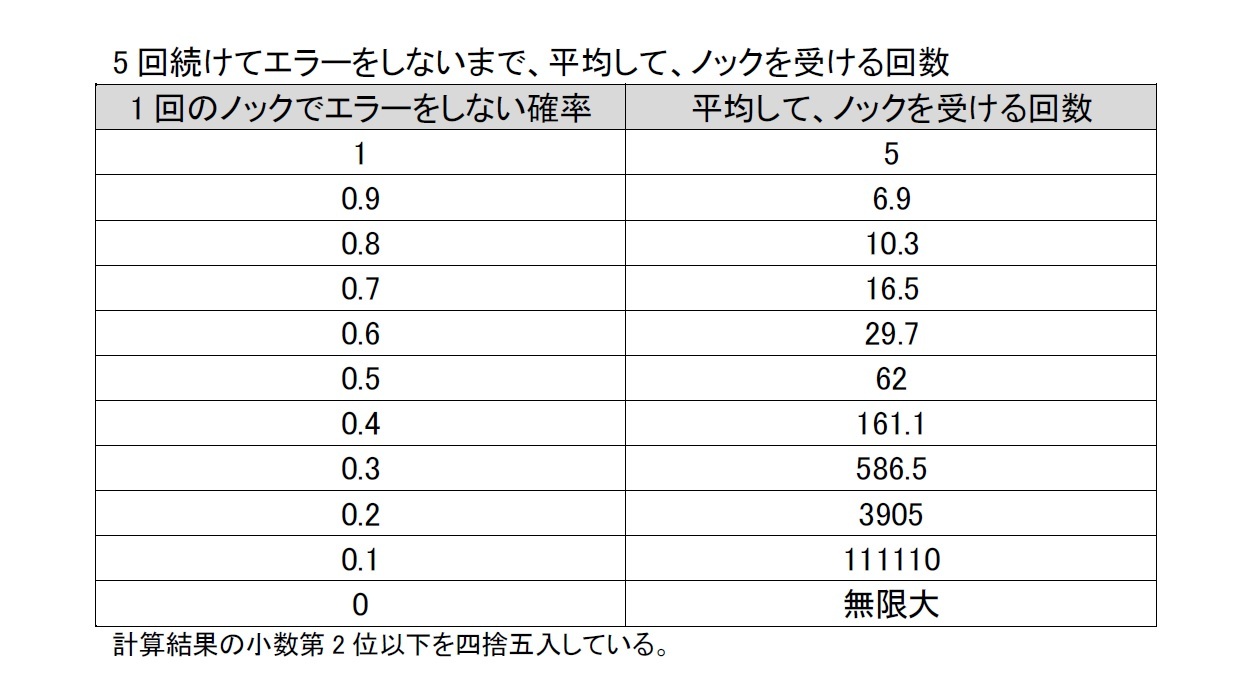
pが0.5の場合、つまり、1回のノックでエラーをしないかするかが半分ずつの場合、先ほどのコイン投げと同じことになる。その計算結果から、5回続けてエラーをしないまでに、平均して、62回のノックが必要となる。

では、pが0.5以外の場合はどうか? コイン投げと同様に、連立方程式を解いて、計算することになる。

いまノックを受けていて、k回続けてエラーをしていない状態だとしよう。この状態から、平均して、あとz_k回ノックを受けたら、5回続けてエラーをしない状態に至って練習が終了する。kの範囲は、0～4だ。

このとき、つぎの5つの関係式を作ることができる。

z₀　＝　1 ＋ p × z₁ ＋ (1-p) × z₀　…　(11)
z₁　＝　1 ＋ p × z₂ ＋ (1-p) × z₀　…　(12)
z₂　＝　1 ＋ p × z₃ ＋ (1-p) × z₀　…　(13)
z₃　＝　1 ＋ p × z₄ ＋ (1-p) × z₀　…　(14)
z₄　＝　1 ＋ (1-p) × z₀　 …　(15)

確率として、0.5の代わりに、pや(1-p) を用いた式となっている。(11)～(15)を解くと、次の通りとなる。

z₀　＝　{(1/p)⁵ － 1} / (1-p)
z₁　＝　{(1/p)⁵ － 1/p} / (1-p)
z₂　＝　{(1/p)⁵ － (1/p)²} / (1-p)
z₃　＝　{(1/p)⁵ － (1/p)³} / (1-p)
z₄　＝　{(1/p)⁵ － (1/p)⁴} / (1-p)

一応、連立方程式は解けたが、何とも、おどろおどろしい感じの結果となり実感がわいてこない。そこで、実際に、pに値を代入して、計算をしてみる。

守備が上手な選手で、1回のノックでエラーをしない確率が0.8の場合、平均して、10回程度のノックで終了となる。

問題は、この練習法を、守備が下手な選手に用いる場合だ。1回のノックでエラーをしない確率が0.3の場合、平均回数は500回を超える。この確率が0.2の場合は、3900回を超える。こうなると、ノックを受ける選手にとっても、ノックをするコーチにとっても、まさに“地獄の猛特訓”となる。

注意すべきなのは、この計算では、1回1回のノックでエラーをしない事象(またはエラーをする事象)は独立である、と暗黙のうちに仮定している点だ。実際には、何回もノックを受けるうちに、守備が上手くなっていき、5回続けてエラーをしないまでの平均回数は減っていくかもしれない。

だが、逆のことも考えられる。ノックを繰り返すうちに、疲労がたまったり、集中力が低下していったりして、エラーをしやすくなるというケースだ。また、1度エラーをすると、2度も3度もエラーをしてしまう、いわゆる「エラー癖がつく」ということもあるかもしれない。こうなると、平均して、この表の計算結果よりも、さらに多くのノックの回数が必要となる。

「5回連続で成功したら、今日の練習は、お仕舞いにしましょう」― こういう練習法は、プレーヤーの技術をよく考えて行わないと大変なことになる。

コーチは、選手、プレーヤーの力量を把握したうえで、適切な指導を行うべきと言えるだろう。

(参考文献)

“Mathematical Puzzles” Peter Winkler (CRC Press, 2021)

「コイン投げで4回連続の表」坂井公 (パズルの国のアリス, SCIENTIFIC AMERICAN日本版・日経サイエンスホームページ)
https://www.nikkei-science.com/page/magazine/alice/202108/question.html
https://www.nikkei-science.com/page/magazine/alice/202108/answer.html

日付	タイトル	執筆者	媒体
2025/04/28	リスクアバースの原因－やり直しがきかないとリスクはとれない	篠原拓也	研究員の眼
2025/04/22	審査の差の定量化－審査のブレはどれくらい?	篠原拓也	研究員の眼
2025/04/15	患者数:入院は減少、外来は増加－2023年の「患者調査」にコロナ禍の影響はどうあらわれたか?	篠原拓也	基礎研レター
2025/04/08	センチネル効果の活用－監視されていると行動が改善する?	篠原拓也	研究員の眼

日付

タイトル

執筆者

媒体

2025/04/28

リスクアバースの原因－やり直しがきかないとリスクはとれない

篠原拓也

研究員の眼

2025/04/22

審査の差の定量化－審査のブレはどれくらい?

篠原拓也

研究員の眼