コンプリートまでの買い物回数－レアアイテムが加わると回数が増える

保険研究部主席研究員兼気候変動リサーチセンターチーフ気候変動アナリスト兼ヘルスケアリサーチセンター主席研究員篠原拓也

このレポートの関連カテゴリ

何か好きな物を集めたいというのは、人間の持っている本性の1つかもしれない。

昔から、ある一連の物を蒐集(しゅうしゅう)することを趣味とする人は数多くいる。いわゆる“コレクター”と呼ばれる人だ。コレクターは、ときどき集めた物をうっとりと眺めることで、至福のときを過ごすという。

ひとくちにコレクターといっても、集める対象はさまざまだ。代表的なものとして、絵画、造形といった美術品や骨董品、工芸品などが挙げられる。コインや切手や切符などの蒐集も王道といえるだろう。野球やサッカーなどのスポーツの選手カードにも根強い人気がある。アニメなどのキャラクター関連のアイテムもさまざまな種類があり、多くのコレクターを惹きつけている。

このうち、昔から、選手カードやキャラクター関連のアイテムは、お菓子のおまけとして提供されてきた。また、日本では1970年代から、カプセル自動販売機(いわゆる「ガチャガチャ」)も普及している。現在は、カプセルトイとして、さまざまな種類のアイテムが提供されるようになっている。

選手カードやキャラクターアイテムなどには、買うものを自分で選べない、という特徴がある。誰の選手カードが入っているか、どのキャラクターアイテムがゲットできるかは、実際にお菓子を買ってみたり、カプセルトイを取り出してみたりするまでわからない。そのドキドキ感が、魅力につながっているともいえる。

ただし、このシステムだと、ある一連の物をすべて集める、すなわちコンプリートするまで、何回も買い物をしないといけない、という事態が生じる。今回は、コンプリートまでの買い物の回数について、確率をもとに考えいくことにしよう。

◇ 「大人買い」では対応不能と想定する

まず、「○○回買えば、絶対にコンプリートできる」ということは想定しないことにしよう。

最近は、よく「大人買い」と称して、おまけのついたお菓子を大量に買い込むケースが見られる。子どものときに、おこづかいが少なくて集めるのに苦労したアイテムを、大人になったいま、大金をもとに一気に蒐集してしまおうという行動だ。

大人買いは、いっぺんに多くのアイテムを得ることができて気持ちがよいが、あっさりとコンプリートしてしまった後には、どこか味気なさも残るものかもしれない。

この大人買いが成立するためには、“段ボール1カートン分”などと、一定数のお菓子を大量に買うことで、必ず全てのアイテムがゲットできるという前提がある。アイテムを製造、提供するメーカー側の事情もあって、そのようなことになるのだろうが、これでは、確率の出番がない。

そこで、こうした事情はいったん脇に置いて、「○○回買えば、絶対にコンプリートできる」ということは想定しないことにする。純粋に確率的に見れば、100％の確率でコンプリートするために必要となる買い物の回数は、無限大ということになる。

無限大の回数について考えるのは簡単ではない。そこで、本稿では、コンプリートまでの買い物回数の平均値(平均買い物回数)について、検討していくことにしよう。

◇ “発生確率p” の事象が起きるまでの平均回数はpの逆数

ここで、確率と平均回数に関する命題を1つ挙げておこう。「“発生確率p”の事象が起きるまでの平均回数はpの逆数(p分の1)」というものだ。

たとえば、ある自然災害が年間1%の確率、つまり100年に1度の確率で発生するとした場合、その災害が発生するまでの平均年数は0.01分の1で100年、というものだ。

読者からは「そんなことは当たり前だろう」という声が聞こえてきそうだ。だが、高校の数学では、こういう当たり前に見えることも、キッチリと計算して確認する。(以下、少し記号を使った計算をするが、「当たり前だろう」という読者は、次節まで読み飛ばしていただいても構わない。)

平均買い物回数は、1回、2回、3回、4回、… の各回数に、それぞれの確率を掛け算して、それらをすべて合計して計算される。平均買い物回数をＳとすれば、つぎのような計算式となる。

Ｓ＝　1×p　＋　2×(1-p)p　＋　3×(1-p)²p　＋　4×(1-p)³p　＋　…

こういう数列の和が出てきたら、両辺を(1-p)倍して、次のようにする。

(1-p)Ｓ＝　1×(1-p)p　＋　2×(1-p)²p　＋　3×(1-p)³p　＋　4×(1-p)⁴p　＋　…

辺ごとに、第一の算式から第二の算式を引き算すると、次のようになる。

(左辺)　＝Ｓ－ (1-p)Ｓ　＝　pＳ

(右辺)　＝{ 1×p　＋　2×(1-p)p　＋　3×(1-p)²p　＋　4×(1-p)³p　＋　…　}
　　　　　　　－ { 1×(1-p)p　＋　2×(1-p)²p　＋　3×(1-p)³p　＋　4×(1-p)⁴p　＋　…}

　　　　＝　   p　＋　　 (1-p)p　＋　   (1-p)²p　＋　   (1-p)³p　＋     (1-p)⁴p　＋　…

　　　　＝　   p　×　{　1　＋　(1-p)　＋　(1-p)²　＋　(1-p)³　＋　(1-p)⁴　＋　…　}

　　　　＝　   p　×　1／{ 1 － (1-p)}

　　　　＝　   1

(左辺)　＝ (右辺)として、Ｓ＝1/p　が得られる。なお数学では、厳密には、数列の和がある一定の水準に収束することが、こういう計算ができるための前提条件となるが、いまはこれ以上細かいことは気にしないでおくことにしよう。

◇ 6種類のアイテムをコンプリートするためには、平均的に14.7回の買い物が必要

それでは、コンプリートするまでの平均買い物回数の計算をしてみよう。全部でn種類のアイテムがあって、それを全部買い揃えるものとする。1回の買い物で各アイテムがゲットできる確率はどれも同じで1/nずつ、と仮定しよう。

まず、1種類目のアイテム。1回買い物をすれば、どれかの種類のアイテムが必ず手に入る。したがって、1種類目のアイテムをゲットするには、1回の買い物で達成できる。

次に、2種類目のアイテム。通算2回目の買い物で、2種類目がゲットできればよいが、運悪く1種類目と同じものが手に入ることもある。2種類目がゲットできる確率は、1種類目と異なるものが出る確率だから、(n-1)/nだ。前節の命題をもとにすると、1種類目のアイテムを手に入れた後、2種類目をゲットするまでの平均回数は、n/(n-1)回ということになる。

続いて、3種類目のアイテム。2種類目を手に入れた後、次の買い物で3種類目がゲットできればよいが、運悪く1種類目や2種類目と同じものが手に入ることもある。3種類目がゲットできる確率は、1種類目や2種類目と異なるものが出る確率だから、(n-2)/nだ。前節の命題をもとにすると、2種類目のアイテムを手に入れた後、3種類目をゲットするまでの平均回数は、n/(n-2)回ということになる。

………

こんな感じで何回も買い物をしてアイテム蒐集を進めていき、(n-1)種類目のアイテムが手に入ったとしよう。この状態で、1回の買い物で、最後に残った1種類のアイテムがゲットできる確率は1/nだ。前節の命題をもとにすると、(n-1)種類目のアイテムを手に入れた後、n種類目をゲットするまでの平均回数は、n回ということになる。

こうして求められた回数を全部足す。結局、全部でn種類のアイテムがあって、それを全部買い揃えるまでの買い物の回数は、以下のような算式で計算できることとなる。

1 ＋ n/(n-1)　＋ n/(n-2) ＋ …　n/2 ＋ n

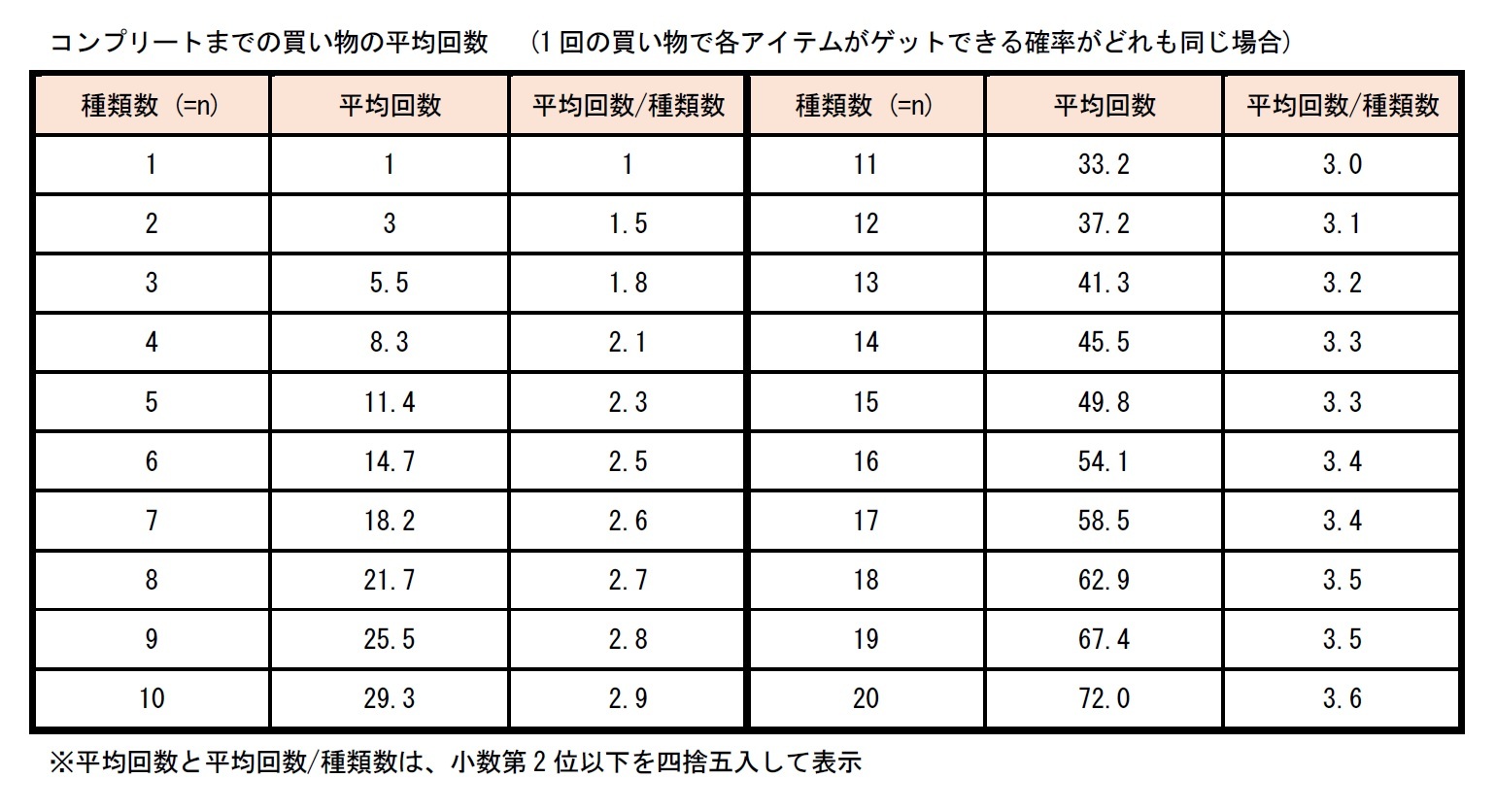
この算式をもとに、アイテムが1～20種類の場合の回数を計算すると、次の表のとおりとなる。

コンプリートまでの買い物の平均回数 (1回の買い物で各アイテムがゲットできる確率がどれも同じ場合)

たとえば、6種類のアイテムをコンプリートするためには、平均的に14.7回の買い物が必要ということになる。種類数と買い物の平均回数の比(平均回数/種類数)は、2.5倍程度となる。

この種類数と買い物の平均回数の比は、種類数が多くなるにつれて徐々に大きくなっている。

この比(平均回数/種類数)でnを無限大にしたものは、数学では「調和級数」と呼ばれるものに相当する。種類数nが増大していくと、この比は、ある水準に収束することなく、(非常にゆっくりとではあるが) 無限大に発散することが知られている。

◇ 激レアアイテムがあると、平均買い物回数は激増する

前節の計算で、種類数が20種類までの場合、コンプリートに必要な買い物の平均回数は、種類数の3.6倍以内にとどまることがわかった。「平均回数がこの程度にとどまるのならば、やっぱり大人買いをして、簡単にコンプリートできる」という気がしてくるかもしれない。

ところが、ここに1つ大きな仮定があった。「1回の買い物で各アイテムがゲットできる確率はどれも同じで1/nずつ」という仮定だ。もし、この仮定が崩れて、各アイテムがゲットできる確率が同じではなかったとしたらどうなるだろうか。つまり、レアアイテムが存在する場合だ。

具体例として、全部で4種類のアイテムがある場合で、これをコンプリートすることを目指す。レアアイテムがなく、1回の買い物で各アイテムがゲットできる確率はどれも25%ずつだとすると、前節の計算結果の表の通り、平均買い物回数は約8.3回となる。

しかし、4種類のアイテムのうち1つがレアもので、1回の買い物でゲットできる確率は10%。残り3つがゲットできる確率はそれぞれ30%ずつとすると、平均買い物回数は約11.9回となる。

もし、4種類のアイテムのうち1つが激レアもので、1回の買い物でゲットできる確率は1%。残り3つがゲットできる確率はそれぞれ33%ずつとすると、平均買い物回数は約100.2回となる。

コンプリートするためには、レアものや激レアもののアイテムが平均何回の買い物でゲットできるかが問題となるため、このように回数が激増するわけだ。

◇ 蒐集熱もほどほどに…

アイテムを製造、提供する側からすると、レアものや激レアもののアイテムは販売に大変効果的だ。コンプリートを目指すコレクターの買い物回数を増加させることができる。SNSを通じて、レアものや激レアものの話題性に火がつけば、さらに販促効果が高まることも期待できる。

コレクターの側からすれば、こういうアイテムのコンプリートに躍起になるうちに、いつのまにか買い物の回数が増えて、買い物の金額が大きく膨らんでしまっている、ということもあるだろう。

こういうふうに蒐集を始めたアイテムがなかなかコンプリートできない場合、少し冷静になってみることも必要かもしれない。

ただ、実際には、頭では理屈を理解していても、「もう1回買い物をすれば、出るかもしれない。もう1回。もう1回だけ…。」などという気がしてしまうことが多い。

特に、“あと1種類出ればコンプリート”という、リーチがかかった状態になると、そこで買い物を止めてコンプリートをあきらめることは簡単ではないだろう。

理屈だけではあきらめきれない ―― これが、人間の本性なのかもしれない。

(参考文献)

“Mathematical Puzzles” Peter Winkler (CRC Press, 2021)

日付	タイトル	執筆者	媒体
2025/03/25	産業クラスターを通じた脱炭素化－クラスターは温室効果ガス排出削減の潜在力を有している	篠原拓也	基礎研レター
2025/03/18	気候変動:アクチュアリースキルの活用－「プラネタリー・ソルベンシー」の枠組みに根差したリスク管理とは?	篠原拓也	基礎研レター
2025/03/11	国民負担率 24年度45.8%の見込み－高齢化を背景に、欧州諸国との差は徐々に縮小	篠原拓也	研究員の眼
2025/03/04	サイバーリスクのモデリング－相互に接続されたシステミックリスクをどうモデリングする?	篠原拓也	保険・年金フォーカス

日付

タイトル

執筆者

媒体

2025/03/25

産業クラスターを通じた脱炭素化－クラスターは温室効果ガス排出削減の潜在力を有している

篠原拓也

基礎研レター

2025/03/18

気候変動:アクチュアリースキルの活用－「プラネタリー・ソルベンシー」の枠組みに根差したリスク管理とは?

篠原拓也

基礎研レター