- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 無限について(その6)-無限級数について-
コラム
2022年11月21日
文字サイズ
- 小
- 中
- 大
なお、有限数列の場合には、和の順番をどのような形に変更しても結果は同じになるが、無限級数の場合には、足す順番も重要で、足し算の順序を変更することはできない。無限級数の和は足す順序を変更することによって、その結果(収束や発散、収束するとしてもその極限値)が変わってくることがある。
無限級数の和の例
収束する無限級数の場合には、有限級数と同様になるが、収束しない無限級数や収束の有無が不明な無限級数の場合には順番が重要になる。以下でその具体例を示す。
具体例(その1)
1-1+1-1+1-1+・・・
この答えをSとした時、もし有限級数と同じような考え方を使用すると、以下のような計算ができることになる。
(1) S=1-(1-1+1-1+1-1+・・・ )
=1-S
∴S=1/2
(2) S=(1-1)+(1-1)+(1-1)+・・・
=0+0+0+・・・
=0
(3) S=1-((1-1)+(1-1)+(1-1)+・・・)
=1-0
=1
具体例(その2)
1-2+4-8+16-32+64-・・・
この答えをSとした時、もし有限級数と同じような考え方を使用すると、以下のような計算ができることになる。
(1) S=1-2(1-2+4-8+16-32+・・・ )
=1-2S
∴S=1/3
(2) S=1+(-2+4)+(-8+16)+(-32+64)+・・・
=1+2+8+32+・・・
=∞
(3) S=(1+4+16+64+・・・)-(2+8+32+・・・ )
=(1+4+16+64+・・・)-2(1+4+16+64+・・・)
=-(1+4+16+64+・・・)
=-∞
これは、どれも間違っている。無限級数の計算では、勝手に括弧記号を使って、足し算の順番を変更することは許されていない。さらに、勝手に収束する値が存在するとの前提を置くことはできない。
上記のケースはいずれも一定の値には収束せず、発散することになる。
一方で、同様に和と差が交互に現れてくる級数でも、以下のケースでは収束することが示される。
具体例(その3)
1-1/2+1/2-1/3+1/3-1/4+1/4-・・・
この級数の場合、
S2n-1=1 S2n=1-1/(n+1)
となることから、いずれにしても1に収束することになる。
具体例(その1)
1-1+1-1+1-1+・・・
この答えをSとした時、もし有限級数と同じような考え方を使用すると、以下のような計算ができることになる。
(1) S=1-(1-1+1-1+1-1+・・・ )
=1-S
∴S=1/2
(2) S=(1-1)+(1-1)+(1-1)+・・・
=0+0+0+・・・
=0
(3) S=1-((1-1)+(1-1)+(1-1)+・・・)
=1-0
=1
具体例(その2)
1-2+4-8+16-32+64-・・・
この答えをSとした時、もし有限級数と同じような考え方を使用すると、以下のような計算ができることになる。
(1) S=1-2(1-2+4-8+16-32+・・・ )
=1-2S
∴S=1/3
(2) S=1+(-2+4)+(-8+16)+(-32+64)+・・・
=1+2+8+32+・・・
=∞
(3) S=(1+4+16+64+・・・)-(2+8+32+・・・ )
=(1+4+16+64+・・・)-2(1+4+16+64+・・・)
=-(1+4+16+64+・・・)
=-∞
これは、どれも間違っている。無限級数の計算では、勝手に括弧記号を使って、足し算の順番を変更することは許されていない。さらに、勝手に収束する値が存在するとの前提を置くことはできない。
上記のケースはいずれも一定の値には収束せず、発散することになる。
一方で、同様に和と差が交互に現れてくる級数でも、以下のケースでは収束することが示される。
具体例(その3)
1-1/2+1/2-1/3+1/3-1/4+1/4-・・・
この級数の場合、
S2n-1=1 S2n=1-1/(n+1)
となることから、いずれにしても1に収束することになる。
これについては、「2つの無限級数がそれぞれAとBに収束し、少なくとも一方の級数が絶対収束するならば、それらのコーシー積はABに収束する」(Mertensの定理)が成り立つことが示されている。
最後に
今回は、無限級数に関する話題について紹介してきた。
無限級数なるものは、日常生活では殆ど関係のないものといえるかもしれないが、実は各種の考え方のベースに無限級数的な概念が存在している。その意味で、何らかの機会に一応気にかけてもらえればと思って、紹介させていただいた。
以上、今回までの6回の研究員の眼で、無限に関する話題について紹介してきた。無限については、さらに幾何学的な面からの捉え方等もあり、その概念は極めて奥深いものがある。今回の6回の比較的身近と思われるテーマを通じて、無限というものに、少しは興味・関心を抱いてもらえればと思った次第である。
無限級数なるものは、日常生活では殆ど関係のないものといえるかもしれないが、実は各種の考え方のベースに無限級数的な概念が存在している。その意味で、何らかの機会に一応気にかけてもらえればと思って、紹介させていただいた。
以上、今回までの6回の研究員の眼で、無限に関する話題について紹介してきた。無限については、さらに幾何学的な面からの捉え方等もあり、その概念は極めて奥深いものがある。今回の6回の比較的身近と思われるテーマを通じて、無限というものに、少しは興味・関心を抱いてもらえればと思った次第である。
(2022年11月21日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
| 2025/09/25 | 数字の「49」に関わる各種の話題-49という数字に皆さんはどんなイメージを有しているのだろう- | 中村 亮一 | 研究員の眼 |
| 2025/09/12 | 数字の「48」に関わる各種の話題-48という数字は、結構いろいろな場面で現れてくるようだ- | 中村 亮一 | 研究員の眼 |
新着記事
-
2025年10月14日
今週のレポート・コラムまとめ【10/7-10/10発行分】 -
2025年10月10日
企業物価指数2025年9月~国内企業物価の上昇率は前年比2.7%、先行きは鈍化予想~ -
2025年10月10日
中期経済見通し(2025~2035年度) -
2025年10月10日
保険・年金関係の税制改正要望(2026)の動き-関係する業界・省庁の改正要望事項など -
2025年10月10日
若者消費の現在地(4)推し活が映し出す、複層的な消費の姿~データで読み解く20代の消費行動
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【無限について(その6)-無限級数について-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
無限について(その6)-無限級数について-のレポート Topへ



















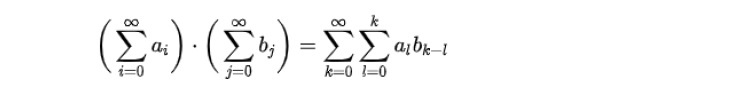

 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




