- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 無限について-無限に関するパラドックス(3)-
コラム
2022年09月28日
文字サイズ
- 小
- 中
- 大
はじめに
研究員の眼「無限について―無限に関するパラドックス(1)」で、有名なゼノンのパラドックスの「アキレスと亀」及び「飛んでいる矢は止まっている」について紹介し、「有限と無限」の関係、さらには「実無限と可能無限」の考え方について紹介した。また、研究員の眼「無限について―無限に関するパラドックス(2)」では、「ヒルベルトの無限ホテル」や「部分と全体が同じ」ということで、無限集合の特質及び濃度の概念について紹介した。
今回は、無限に関するパラドックス(3)ということで、前回の研究員の眼で紹介できなかった無限集合に関する有名なパラドックスについて紹介するとともに、これらのパラドックスの背景にある素朴集合論と公理的集合論に関して、私なりの理解に基づいて、簡単に紹介していきたいと思っている。
今回は、無限に関するパラドックス(3)ということで、前回の研究員の眼で紹介できなかった無限集合に関する有名なパラドックスについて紹介するとともに、これらのパラドックスの背景にある素朴集合論と公理的集合論に関して、私なりの理解に基づいて、簡単に紹介していきたいと思っている。
カントールのパラドックス
ゲオルグ・カントール(Georg Cantor)は、後に説明するいわゆる素朴集合論の確立者で、前回の研究員の眼で説明したように濃度の概念を導入しているが、彼に因むパラドックスとして、「カントールのパラドックス」と呼ばれるものがある。これは、「集合全体の集合(全ての集合の集合)」を考えることによって、出てくる次のようなパラドックスである。
・全ての集合の集合Xを考える。すると、前回の研究員の眼で紹介したように、その冪集合(部分集合全体の集合)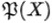 (あるいは2X )は、カントールの定理によって、より大きな濃度を有することになる。一方で、
(あるいは2X )は、カントールの定理によって、より大きな濃度を有することになる。一方で、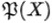 は、集合としてXに含まれることになるため、その濃度はXの濃度以下となるはずである。 ここに矛盾が生じることになる。
は、集合としてXに含まれることになるため、その濃度はXの濃度以下となるはずである。 ここに矛盾が生じることになる。
これはまた、濃度が順序付けられていて(2つの集合の濃度の大小関係がわかる)、「最大の濃度(の集合)は存在しない。」という定理から「全ての濃度の集合は存在しない」と言うことができる。
・全ての集合の集合Xを考える。すると、前回の研究員の眼で紹介したように、その冪集合(部分集合全体の集合)
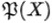 (あるいは2X )は、カントールの定理によって、より大きな濃度を有することになる。一方で、
(あるいは2X )は、カントールの定理によって、より大きな濃度を有することになる。一方で、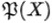 は、集合としてXに含まれることになるため、その濃度はXの濃度以下となるはずである。 ここに矛盾が生じることになる。
は、集合としてXに含まれることになるため、その濃度はXの濃度以下となるはずである。 ここに矛盾が生じることになる。これはまた、濃度が順序付けられていて(2つの集合の濃度の大小関係がわかる)、「最大の濃度(の集合)は存在しない。」という定理から「全ての濃度の集合は存在しない」と言うことができる。
ラッセルのパラドックス
「ラッセルのパラドックス」というのは、「自分自身を要素として含まない集合全体の集合」を考えることによって出てくるパラドックスである。バートランド・ラッセル(Bertrand Russell)は、英国の哲学者、論理学者、数学者であり、1950年には哲学の分野でノーベル文学賞を受賞している。
具体的には、Xを集合として、R={X|X ∉ X}(即ち、Rは「自分自身を要素として含まない集合X全体の集合」)とする1。
この時、R自身も集合とすると、Rは、自分自身を要素として含むかどうかを決定できない。
即ち、R ∊ R とすると、Rの定義によりR ∉ Rとなるから、これは矛盾する。従って、R ∉ Rとなるが、この時Rの定義により、R ∊ Rとなって、これも矛盾することになる。
あるいは、別の言い方をすれば、「自分自身を要素として含まない集合全体の集合」を作ったとしても、この集合自身が先の「自分自身を要素として含まない集合全体の集合」に含まれない、新しい「自分自身を要素として含まない集合」となってしまい、同じプロセスを繰り返していくことで、「自分自身を要素として含まない集合全体の集合」自体が無限に拡大していくことになってしまう2。
この「ラッセルのパラドックス」については、一般の人にも馴染みやすく分かり易くしたものとして、例えば、以下のようなパラドックスとして紹介されることも多い。
1 {a}を「aを要素とする集合」とすると、aと{a}は異なるので、{a}∉{a}となるので、「自分自身を要素として含まない集合」となる。例えば、「猫の集合」は集合であるが、「猫の集合」というものは「猫の集合」の要素には含まれないので、「自分自身を要素として含まない集合」となる。
2 同じことが、「自分自身を要素として含む集合」にも言える。則ち、例えば「猫でないものの集合」を考えると、「猫でないものの集合」自体も「猫でないものの集合」に該当するので、これは一見すると「自分自身を要素として含む集合」になっていると思われるかもしれない。ところが、この新たな「猫でないものの集合」は元々の「猫でないものの集合」には含まれていないので、その意味で「自分自身を要素として含んでいる」とは言えないことになる。そこで、この新たな「猫でないものの集合」を元々の「猫でないものの集合」に加えたものを新たな「猫でないものの集合」として考えたとしても、同じことが繰り返されていき、「猫でないものの集合」自体が無限に拡大していくことになってしまう。
具体的には、Xを集合として、R={X|X ∉ X}(即ち、Rは「自分自身を要素として含まない集合X全体の集合」)とする1。
この時、R自身も集合とすると、Rは、自分自身を要素として含むかどうかを決定できない。
即ち、R ∊ R とすると、Rの定義によりR ∉ Rとなるから、これは矛盾する。従って、R ∉ Rとなるが、この時Rの定義により、R ∊ Rとなって、これも矛盾することになる。
あるいは、別の言い方をすれば、「自分自身を要素として含まない集合全体の集合」を作ったとしても、この集合自身が先の「自分自身を要素として含まない集合全体の集合」に含まれない、新しい「自分自身を要素として含まない集合」となってしまい、同じプロセスを繰り返していくことで、「自分自身を要素として含まない集合全体の集合」自体が無限に拡大していくことになってしまう2。
この「ラッセルのパラドックス」については、一般の人にも馴染みやすく分かり易くしたものとして、例えば、以下のようなパラドックスとして紹介されることも多い。
1 {a}を「aを要素とする集合」とすると、aと{a}は異なるので、{a}∉{a}となるので、「自分自身を要素として含まない集合」となる。例えば、「猫の集合」は集合であるが、「猫の集合」というものは「猫の集合」の要素には含まれないので、「自分自身を要素として含まない集合」となる。
2 同じことが、「自分自身を要素として含む集合」にも言える。則ち、例えば「猫でないものの集合」を考えると、「猫でないものの集合」自体も「猫でないものの集合」に該当するので、これは一見すると「自分自身を要素として含む集合」になっていると思われるかもしれない。ところが、この新たな「猫でないものの集合」は元々の「猫でないものの集合」には含まれていないので、その意味で「自分自身を要素として含んでいる」とは言えないことになる。そこで、この新たな「猫でないものの集合」を元々の「猫でないものの集合」に加えたものを新たな「猫でないものの集合」として考えたとしても、同じことが繰り返されていき、「猫でないものの集合」自体が無限に拡大していくことになってしまう。
床屋のパラドックス
これは、次のようなパラドックスである3。
・ある村でただ一人の床屋は、自分で髭を剃らない村人の髭を剃り、自分で髭を剃る村人の髭は剃らない。この時、床屋自身の髭は誰が剃ることになるのか。
床屋が自分の髭を剃らなければ、彼は「自分で髭を剃らない村人」になるので、床屋は自分の髭を自分で剃らなくてはいけなくなり、矛盾が生じる。
床屋が自分の髭を剃るならば、彼は「自分で髭を剃る村人」になるので、自分で髭を剃る村人の髭を剃らないということに矛盾する。
したがって、いずれにしても矛盾が生ずることになる。
これは、ラッセルのパラドックスにおいて、Xを「自分で髭を剃る村人(の集合)」とした場合に相当している。
3 「床屋」は「理髪師」又は「理容師」(性別を問わない)というのがより適切な表現かもしれないが、ここでは一般的にこのパラドックスの紹介で使用される「床屋」の表現を使用している。
・ある村でただ一人の床屋は、自分で髭を剃らない村人の髭を剃り、自分で髭を剃る村人の髭は剃らない。この時、床屋自身の髭は誰が剃ることになるのか。
床屋が自分の髭を剃らなければ、彼は「自分で髭を剃らない村人」になるので、床屋は自分の髭を自分で剃らなくてはいけなくなり、矛盾が生じる。
床屋が自分の髭を剃るならば、彼は「自分で髭を剃る村人」になるので、自分で髭を剃る村人の髭を剃らないということに矛盾する。
したがって、いずれにしても矛盾が生ずることになる。
これは、ラッセルのパラドックスにおいて、Xを「自分で髭を剃る村人(の集合)」とした場合に相当している。
3 「床屋」は「理髪師」又は「理容師」(性別を問わない)というのがより適切な表現かもしれないが、ここでは一般的にこのパラドックスの紹介で使用される「床屋」の表現を使用している。
市長のパラドックス
これは、次のようなパラドックスである。
・自分が市長をしている市に住んでいない市長を「不在市長」と呼ぶ。全ての不在市長で構成される「不在市長市」を作ったとする時、不在市長市の市長はどこに住めばよいか。
不在市長市の市長Aが不在市長市に住むと、Aは自らが市長をしている市に住むこととなり、不在市長ではなくなるため、矛盾が生じる。
Aが不在市長市以外の市に住むと、Aは自らが市長をしている市には住んでないため、不在市長となるが、「不在市長市に全ての不在市長が住む」に矛盾する。
したがって、どちらにしても矛盾が生じることになる。
これは、ラッセルのパラドックスにおいて、Xを「不在市長(の集合)」とした場合に相当している。
・自分が市長をしている市に住んでいない市長を「不在市長」と呼ぶ。全ての不在市長で構成される「不在市長市」を作ったとする時、不在市長市の市長はどこに住めばよいか。
不在市長市の市長Aが不在市長市に住むと、Aは自らが市長をしている市に住むこととなり、不在市長ではなくなるため、矛盾が生じる。
Aが不在市長市以外の市に住むと、Aは自らが市長をしている市には住んでないため、不在市長となるが、「不在市長市に全ての不在市長が住む」に矛盾する。
したがって、どちらにしても矛盾が生じることになる。
これは、ラッセルのパラドックスにおいて、Xを「不在市長(の集合)」とした場合に相当している。
ラッセルのパラドックスを解決するには
これらのパラドックスは、いわゆる「自己言及のパラドックス」4を引き起こしているものといえる。これを解決するには、例えば、以下のように問題の前提等を変更することが必要になってくる。
(1) ラッセルのパラドックスについては、任意の集合の集合 X について、「Xの要素のうちで自分自身を要素として含まない集合の集合」はXの要素として見つけることはできず、Xの外にのみ、そのような集合を見つけることができることから、このようなXを集合とは異なるものと位置づける。
(2) 床屋のパラドックスについては、「床屋は村人ではない(例えば隣の村の人である)」とする。
(3) 不在市長市の市長は、いわゆる他の不在市長とは異なる存在である、と位置付ける。
いずれにしても、自己言及とならないように、自己に相当するものを現在対象としているものとは別のものと整理することが必要になってくる。
4 「自己言及のパラドックス」としては、「嘘つきのパラドックス」と呼ばれる「私は嘘つきである」あるいは「クレタ人はいつも嘘をつく」というものがある。私が嘘つきならば、私が嘘つきであると言っているのは嘘となり、私は嘘つきではないということになる。一方で、私が嘘つきでないならば、私は嘘つきであるというは嘘でないことになり、私は嘘つきと言うことになる。いずれにしても、矛盾が発生することになる。
(1) ラッセルのパラドックスについては、任意の集合の集合 X について、「Xの要素のうちで自分自身を要素として含まない集合の集合」はXの要素として見つけることはできず、Xの外にのみ、そのような集合を見つけることができることから、このようなXを集合とは異なるものと位置づける。
(2) 床屋のパラドックスについては、「床屋は村人ではない(例えば隣の村の人である)」とする。
(3) 不在市長市の市長は、いわゆる他の不在市長とは異なる存在である、と位置付ける。
いずれにしても、自己言及とならないように、自己に相当するものを現在対象としているものとは別のものと整理することが必要になってくる。
4 「自己言及のパラドックス」としては、「嘘つきのパラドックス」と呼ばれる「私は嘘つきである」あるいは「クレタ人はいつも嘘をつく」というものがある。私が嘘つきならば、私が嘘つきであると言っているのは嘘となり、私は嘘つきではないということになる。一方で、私が嘘つきでないならば、私は嘘つきであるというは嘘でないことになり、私は嘘つきと言うことになる。いずれにしても、矛盾が発生することになる。
素朴集合論と公理的集合論
さて、これらのパラドックスは、「素朴集合論(Naive set theory)」と呼ばれる集合論におけるパラドックスとして、有名なものである。
「素朴集合論」は、「公理的集合論」とは異なり、形式化されておらず、自然言語(人間が意思疎通のために日常的に用いる言語)を使用して、集合等が定義される。任意の性質を用いて、制限なしに集合を構築できるため、パラドックスを生み出すことになっている。
これに対応するのが「公理的集合論(axiomatic set theory)」と呼ばれるもので、これは形式的な論理を用いて定義される、公理化された集合論のことを言う。現在一般的に使われている集合の公理系としては「ツェルメロ=フレンケル集合論(ZF公理系)」又はZF公理系に選択公理(Axiom of Choice)と呼ばれるものを加えた「ZFC公理系(選択公理付きのZF公理系)」と呼ばれるものがある。ここで、「選択公理」というのは、「X が互いに交わらないような空でない集合の集合であるとき、X の各要素から一つずつ要素をとってきたような集合(選択集合)が存在する。」というものである。さらには、「フォン・ノイマン=ベルナイス=ゲーデル集合論(NBG)」と呼ばれるものもある。
「素朴集合論」は、「公理的集合論」とは異なり、形式化されておらず、自然言語(人間が意思疎通のために日常的に用いる言語)を使用して、集合等が定義される。任意の性質を用いて、制限なしに集合を構築できるため、パラドックスを生み出すことになっている。
これに対応するのが「公理的集合論(axiomatic set theory)」と呼ばれるもので、これは形式的な論理を用いて定義される、公理化された集合論のことを言う。現在一般的に使われている集合の公理系としては「ツェルメロ=フレンケル集合論(ZF公理系)」又はZF公理系に選択公理(Axiom of Choice)と呼ばれるものを加えた「ZFC公理系(選択公理付きのZF公理系)」と呼ばれるものがある。ここで、「選択公理」というのは、「X が互いに交わらないような空でない集合の集合であるとき、X の各要素から一つずつ要素をとってきたような集合(選択集合)が存在する。」というものである。さらには、「フォン・ノイマン=ベルナイス=ゲーデル集合論(NBG)」と呼ばれるものもある。
パラドックスの解消に向けて
「素朴集合論」の世界で、例えば「集合全体の集合X」というようなものを考えると、これまで述べてきたように、これをXの中に求めることができなくなり、それはXの外にある存在ということになってしまう。この論理は繰り返されていくので、どのようにXを拡張していっても、Xの要素で構成される集合で、Xの要素では表されないものが発生してくることになる。即ち、素朴集合論の中では、形式的にはそのような集合を考えることはできるが、実質的にはそのような集合を考えることは適切でない、ということになる。そのような集合を、他の集合と同じ種類のものとして認めないことをしなければ、パラドックスが発生することになる。
そこで、「集合」というものを明確に定義し、公理を設定して、その公理から導かれる性質のみを使用して、集合を取り扱おうとするものが「公理的集合論」ということになる。
より具体的には、素朴集合論で置かれている以下の「内包公理(Axiom of comprehension)」があるために、カントールのパラドックスやラッセルのパラドックスにおける「集合全体の集合」や「自分自身を要素として含まない集合全体の集合」のようなものが集合として構成できることになる。
「xに関する任意の性質P(x)に対して、P(x) を満たすx の集合 { x|P(x) } が存在する。」
そこで、公理的集合論では、内包公理を、以下の「分出公理(Axiom schema of specification)」に置き換えて、P(x)だけでなく、集合Aの存在を必要とすることで、カントールのパラドックスやラッセルのパラドックスにおけるようなものが集合として存在しないようにしている。
「集合Aの元xに関する任意の性質P(x)に対して、P(x)を満たすAの元xの集合{x∊A|P(x) }が存在する。」
なお、ZFC集合論では、分出公理は公理とされておらず、「置換公理(Axiom schema of replacement)」と呼ばれるものが設けられている(分出公理は置換公理から導ける)。
「公理的集合論」については、別の機会があればということで、これ以上の話はしないことにする5。
5 なお、実は、ZFC集合論の無矛盾性が証明されていないので、ZFC集合論がパラドックスを回避できていることも証明されていない、と言われている。
そこで、「集合」というものを明確に定義し、公理を設定して、その公理から導かれる性質のみを使用して、集合を取り扱おうとするものが「公理的集合論」ということになる。
より具体的には、素朴集合論で置かれている以下の「内包公理(Axiom of comprehension)」があるために、カントールのパラドックスやラッセルのパラドックスにおける「集合全体の集合」や「自分自身を要素として含まない集合全体の集合」のようなものが集合として構成できることになる。
「xに関する任意の性質P(x)に対して、P(x) を満たすx の集合 { x|P(x) } が存在する。」
そこで、公理的集合論では、内包公理を、以下の「分出公理(Axiom schema of specification)」に置き換えて、P(x)だけでなく、集合Aの存在を必要とすることで、カントールのパラドックスやラッセルのパラドックスにおけるようなものが集合として存在しないようにしている。
「集合Aの元xに関する任意の性質P(x)に対して、P(x)を満たすAの元xの集合{x∊A|P(x) }が存在する。」
なお、ZFC集合論では、分出公理は公理とされておらず、「置換公理(Axiom schema of replacement)」と呼ばれるものが設けられている(分出公理は置換公理から導ける)。
「公理的集合論」については、別の機会があればということで、これ以上の話はしないことにする5。
5 なお、実は、ZFC集合論の無矛盾性が証明されていないので、ZFC集合論がパラドックスを回避できていることも証明されていない、と言われている。
「クラス」という概念
「公理的集合論」では、「集合全体の集まり」は集合ではなくて、例えばフォン・ノイマン=ベルナイス=ゲーデル集合論(NBG)では、「クラス(class)」又は「類」と呼ばれ、さらにクラスであって集合でないものを「真のクラス(proper class)」と呼んでいる。
これによれば、先の素朴集合論におけるパラドックスは、「全てのクラスが集合である」という正しくない仮定により発生しているものである、と説明されることになる。その意味において、ラッセルのパラドックスはパラドックスではなくて、R={X|X ∉ X}が集合ではなく、真のクラスであることを証明している、とも言われる。
これによれば、先の素朴集合論におけるパラドックスは、「全てのクラスが集合である」という正しくない仮定により発生しているものである、と説明されることになる。その意味において、ラッセルのパラドックスはパラドックスではなくて、R={X|X ∉ X}が集合ではなく、真のクラスであることを証明している、とも言われる。
最後に
今回は、「無限に関するパラドックス(3)」ということで、前回の研究員の眼で紹介できなかった無限集合に関する有名なパラドックス、及びこれらのパラドックスの背景にある素朴集合論と公理的集合論に関して、簡単に紹介してきた。
今回のパラドックスは、これまでのパラドックスと比べると、ややわかりにくかったのではないかと思われる。数学だけでなく、論理学や哲学の要素が含まれていると感じられただろう。その意味では、やっぱり数学は難しいよね、という印象を持たれた方もいらっしゃるかもしれない。その点は、私の説明が不十分だったということで、ご容赦願いたい。
今回のパラドックスは、これまでのパラドックスと比べると、ややわかりにくかったのではないかと思われる。数学だけでなく、論理学や哲学の要素が含まれていると感じられただろう。その意味では、やっぱり数学は難しいよね、という印象を持たれた方もいらっしゃるかもしれない。その点は、私の説明が不十分だったということで、ご容赦願いたい。
(2022年09月28日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
新着記事
-
2025年10月31日
交流を広げるだけでは届かない-関係人口・二地域居住に求められる「心の安全・安心」と今後の道筋 -
2025年10月31日
ECB政策理事会-3会合連続となる全会一致の据え置き決定 -
2025年10月31日
2025年7-9月期の実質GDP~前期比▲0.7%(年率▲2.7%)を予測~ -
2025年10月31日
保険型投資商品の特徴を理解すること(欧州)-欧州保険協会の解説文書 -
2025年10月31日
鉱工業生産25年9月-7-9月期の生産は2四半期ぶりの減少も、均してみれば横ばいで推移
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【無限について-無限に関するパラドックス(3)-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
無限について-無限に関するパラドックス(3)-のレポート Topへ



















 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




