- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 無限について-無限に関するパラドックス(4)-ガブリエルのラッパ-
コラム
2022年10月11日
文字サイズ
- 小
- 中
- 大
はじめに
無限に関する前回までの3回の研究員の眼では、無限に関するパラドックスを紹介してきた。今回紹介する「ガブリエルのラッパ」と呼ばれるものも無限に関する1種のパラドックスを示すものとなっている。なお、関連するトピックスについては、以前の「フラクタル」に関する研究員の眼「フラクタルって知っていますか-1.26次元や1.58次元の図形ってどんなものなのだろう-」(2021.6.28)でも報告しているので、そちらも参照していただきたい。
ガブリエルのラッパとは
英語をそのまま訳せば「ガブリエルのホルン」ということになるのだろうが、その形から、いわゆる現在我々が「ホルン」と聞いてイメージする楽器とは異なることから、一般的には「ガブリエルのラッパ」あるいは「ガブリエルのトランペット」と呼ばれている。「ガブリエル(Gabriel)」1というのは、キリスト教において、最後の審判のときにラッパを鳴らし、死者を甦らせる天使である。聖書においてガブリエルは「神の言葉を伝える天使」であり、ガブリエルという名前は、ヘブライ語で「神の人」という意味を有している。
なお、「ガブリエルのラッパ」は、この図形を調べた最初の人である17世紀のイタリアの数学者に因んで「トリチェリのトランペット(Torricelli's trumpet)」とも呼ばれている2。
1 ガブリエルは、キリスト教では、イエス・キリストの受胎をマリアに告げる「受胎告知」の役割を有しており、この「受胎告知」のテーマに関しては、フラ・アンジェリコ、ヤン・ファン・エイク、レオナルド・ダ・ビンチ、ボッティチェリ、ティントレット等、数多くの有名な画家による絵画に描かれてきている。
2 エヴァンジェリスタ・トリチェリ(Evangelista Torricelli)は、イタリアの数学者・物理学者・天文学者で、ガリレオ・ガリレイの弟子。液体を入れた容器の側面に比較的小さな穴を空けたときの液体の流出速度に関する「トリチェリの定理」等で有名である。またトリチェリの名が付された小惑星もある。
なお、「ガブリエルのラッパ」は、この図形を調べた最初の人である17世紀のイタリアの数学者に因んで「トリチェリのトランペット(Torricelli's trumpet)」とも呼ばれている2。
1 ガブリエルは、キリスト教では、イエス・キリストの受胎をマリアに告げる「受胎告知」の役割を有しており、この「受胎告知」のテーマに関しては、フラ・アンジェリコ、ヤン・ファン・エイク、レオナルド・ダ・ビンチ、ボッティチェリ、ティントレット等、数多くの有名な画家による絵画に描かれてきている。
2 エヴァンジェリスタ・トリチェリ(Evangelista Torricelli)は、イタリアの数学者・物理学者・天文学者で、ガリレオ・ガリレイの弟子。液体を入れた容器の側面に比較的小さな穴を空けたときの液体の流出速度に関する「トリチェリの定理」等で有名である。またトリチェリの名が付された小惑星もある。
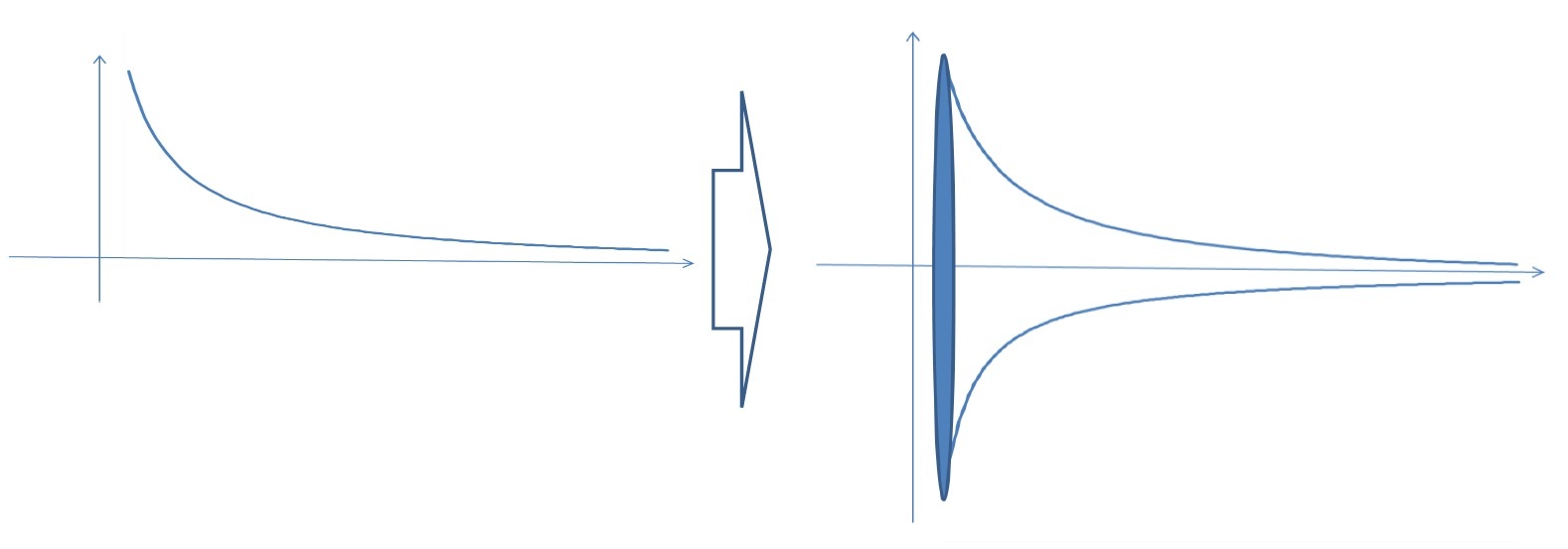
ガブリエルのラッパの定義
2番目の式は(xy平面における)断面積を表している。間の不等号は、「ガブリエルのラッパ」の側面積が断面積より大きいことを示していることになるが、これは図形の形から明らかであろう。
いずれにしても、これにより、「ガブリエルのラッパは、有限な体積と無限の表面積を有する図形」と言うことになる。
なお、「ガブリエルのラッパ」のケースの逆ともいえる「有限の表面積と無限の体積を有する回転体」については、通常は存在しないことが証明される。
いずれにしても、これにより、「ガブリエルのラッパは、有限な体積と無限の表面積を有する図形」と言うことになる。
なお、「ガブリエルのラッパ」のケースの逆ともいえる「有限の表面積と無限の体積を有する回転体」については、通常は存在しないことが証明される。
ガブリエルのラッパ-有限と無限の結び付き
「ガブリエルのラッパ」については、その(xy平面における)断面積は確かに無限大となるが、一方でこれと平行な他の任意の断面は有限な面積しか持たない。従って、各断面の重み付き平均の和としての体積は有限になる、という構造になっている。
まさに、(xy平面において)無限の面積を有する図形を回転させて得られる図形の体積が有限になるという意味において、逆説的(パラドクシカル)なものとなっている。
なお、「ガブリエルのラッパ」という名称は、このように有限と無限が結び付いている状況を、無限が神を表し、「新約聖書」において、「神の言葉を伝える天使」であり、最後の審判を告げる笛を吹くという伝承の大天使ガブリエルになぞらえる形で名付けられたものとなっている。
まさに、(xy平面において)無限の面積を有する図形を回転させて得られる図形の体積が有限になるという意味において、逆説的(パラドクシカル)なものとなっている。
なお、「ガブリエルのラッパ」という名称は、このように有限と無限が結び付いている状況を、無限が神を表し、「新約聖書」において、「神の言葉を伝える天使」であり、最後の審判を告げる笛を吹くという伝承の大天使ガブリエルになぞらえる形で名付けられたものとなっている。
有限な体積と無限の表面積を有する図形のペンキ塗装に関するパラドックス
さて、ここで有名なパラドックスを紹介する。
上記の「ガブリエルのラッパ」をペンキで塗装しようとする。この時に体積は有限なので、「ガブリエルのラッパ」は有限の量のペンキで満たすことができることになる。これにより、「ガブリエルのラッパ」の内側面はペンキで塗装できていることになる。一方で、「ガブリエルのラッパ」の表面積は無限なので、有限の量のペンキで本当に塗りつくすことができるのだろうかと疑問を感じるであろう。
数学的には、ペンキの膜の厚みを限りなく薄くしていけば、無限の面積に対しても有限の量のペンキで塗りつくすことができることになる。ただし、現実にはペンキの薄さには限界があると思われることから、現実的には難しいということになる。ましてや、ペンキの膜の厚さを一定とすれば、無限の表面積を有限の量のペンキで塗り立てることは不可能となる。
上記の「ガブリエルのラッパ」をペンキで塗装しようとする。この時に体積は有限なので、「ガブリエルのラッパ」は有限の量のペンキで満たすことができることになる。これにより、「ガブリエルのラッパ」の内側面はペンキで塗装できていることになる。一方で、「ガブリエルのラッパ」の表面積は無限なので、有限の量のペンキで本当に塗りつくすことができるのだろうかと疑問を感じるであろう。
数学的には、ペンキの膜の厚みを限りなく薄くしていけば、無限の面積に対しても有限の量のペンキで塗りつくすことができることになる。ただし、現実にはペンキの薄さには限界があると思われることから、現実的には難しいということになる。ましてや、ペンキの膜の厚さを一定とすれば、無限の表面積を有限の量のペンキで塗り立てることは不可能となる。
メンガ-のスポンジ-無限の表面積で体積が「0」の図形-
以前の研究員の眼「フラクタルって知っていますか-1.26次元や1.58次元の図形ってどんなものなのだろう-」(2021.6.28)で、2次元超3次元未満のフラクタル図形の例として、「メンガ-のスポンジ」を紹介した。
「メンガ-のスポンジ(Menger sponge)」というのは、以下のプロセスで作成される図形である。
(1) 立方体を、3×3×3の27個の区画に分け、中央(面心・体心)の7個を取り除く。
(2) 残った小さな20個の立方体に対して同じ事を繰り返していく。
「メンガ-のスポンジ」のフラクタル次元は、log20/log3=2.7268 となり、2.72次元の図形ということになる。
「メンガ-のスポンジ」は、1回のプロセスでその表面積が1/3ずつ増加することになるため、その(2次元的な大きさを示す)表面積は無限となる。一方で、1回のプロセスでその体積は7/27ずつ減少することになるため、その(3次元的な大きさを示す)体積は0となる。
すなわち、この「メンガ-のスポンジは、無限の表面積を有しながら、体積が0の図形」ということになる。
「メンガ-のスポンジ(Menger sponge)」というのは、以下のプロセスで作成される図形である。
(1) 立方体を、3×3×3の27個の区画に分け、中央(面心・体心)の7個を取り除く。
(2) 残った小さな20個の立方体に対して同じ事を繰り返していく。
「メンガ-のスポンジ」のフラクタル次元は、log20/log3=2.7268 となり、2.72次元の図形ということになる。
「メンガ-のスポンジ」は、1回のプロセスでその表面積が1/3ずつ増加することになるため、その(2次元的な大きさを示す)表面積は無限となる。一方で、1回のプロセスでその体積は7/27ずつ減少することになるため、その(3次元的な大きさを示す)体積は0となる。
すなわち、この「メンガ-のスポンジは、無限の表面積を有しながら、体積が0の図形」ということになる。
コッホ雪片-周長が無限で面積が有限な図形-
同じく上記の研究員の眼で紹介した「コッホ雪片(Koch snowflake)」は、「無限の周長と有限の面積を有する図形」になっている。
コッホ雪片を形成しているコッホ曲線については、その作り方から、1回の操作で線の長さが4/3倍になっていくことから、コッホ雪片の周長は無限大となるが、一方で、元々の正三角形の面積を1 とするとコッホ雪片の面積は 1.6 に収束する。
コッホ雪片を形成しているコッホ曲線については、その作り方から、1回の操作で線の長さが4/3倍になっていくことから、コッホ雪片の周長は無限大となるが、一方で、元々の正三角形の面積を1 とするとコッホ雪片の面積は 1.6 に収束する。
最後に
今回は、有限と無限の関係についての理解を深めるために、無限の表面積と有限の体積を有する図形について紹介した。これによれば、1つの幾何学的空間図形の上で、有限と無限が並列している、という極めて興味深い結果が得られていることになる。
このようなことが観測されるのは、面積は縦横の二乗の計算で算出されるのに対して、体積は縦横高さの三乗で算出されることに関係しているといえるだろう。1より小さい数の場合、二乗よりも三乗の方が小さくなる。あるいは、体積=面積×高さ なので、面積が無限に収束していっても、高さが無限に小さくなっていけば、体積は有限にもなりうることになる、といえるかもしれない。また、無限級数は、有限の値(極限値)に収束することもあれば、無限大に発散することもある、ということが関係しているといえるかもしれない。
いずれにしても、有限と無限の関係が一筋縄ではいかないことや数学的な考え方と現実の世界での考え方との乖離から、通常の感覚では違和感を覚えるようなパラドックスが生まれてくることになる。
こうしたことを通じて、無限というものに少しでも興味・関心を有してもらえればと思っている。
このようなことが観測されるのは、面積は縦横の二乗の計算で算出されるのに対して、体積は縦横高さの三乗で算出されることに関係しているといえるだろう。1より小さい数の場合、二乗よりも三乗の方が小さくなる。あるいは、体積=面積×高さ なので、面積が無限に収束していっても、高さが無限に小さくなっていけば、体積は有限にもなりうることになる、といえるかもしれない。また、無限級数は、有限の値(極限値)に収束することもあれば、無限大に発散することもある、ということが関係しているといえるかもしれない。
いずれにしても、有限と無限の関係が一筋縄ではいかないことや数学的な考え方と現実の世界での考え方との乖離から、通常の感覚では違和感を覚えるようなパラドックスが生まれてくることになる。
こうしたことを通じて、無限というものに少しでも興味・関心を有してもらえればと思っている。
(2022年10月11日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
| 2025/09/25 | 数字の「49」に関わる各種の話題-49という数字に皆さんはどんなイメージを有しているのだろう- | 中村 亮一 | 研究員の眼 |
| 2025/09/12 | 数字の「48」に関わる各種の話題-48という数字は、結構いろいろな場面で現れてくるようだ- | 中村 亮一 | 研究員の眼 |
新着記事
-
2025年10月14日
今週のレポート・コラムまとめ【10/7-10/10発行分】 -
2025年10月10日
企業物価指数2025年9月~国内企業物価の上昇率は前年比2.7%、先行きは鈍化予想~ -
2025年10月10日
中期経済見通し(2025~2035年度) -
2025年10月10日
保険・年金関係の税制改正要望(2026)の動き-関係する業界・省庁の改正要望事項など -
2025年10月10日
若者消費の現在地(4)推し活が映し出す、複層的な消費の姿~データで読み解く20代の消費行動
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【無限について-無限に関するパラドックス(4)-ガブリエルのラッパ-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
無限について-無限に関するパラドックス(4)-ガブリエルのラッパ-のレポート Topへ



















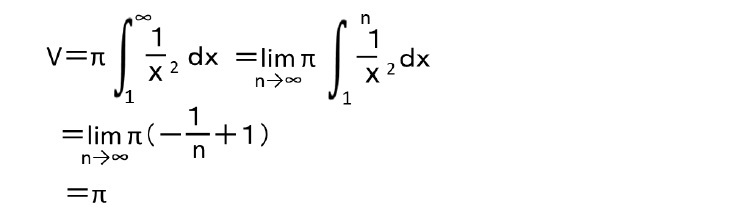
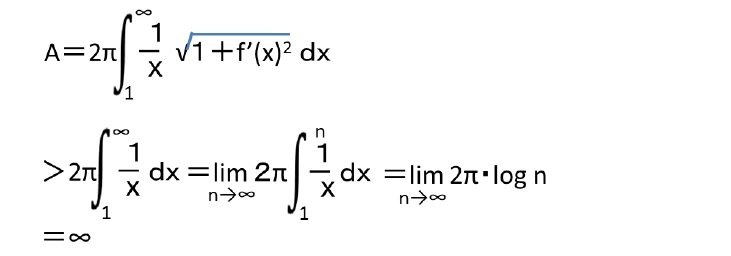


 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




