- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 無限について(その5)-無限大(∞)について-
コラム
2022年10月21日
文字サイズ
- 小
- 中
- 大
はじめに
無限に関する前回までの4回の研究員の眼で、無限に関する代表的なパラドックスのいくつかを紹介してきた。「無限」という場合、その意味合いは必ずしも同じものを指しているとは限らない。前回までの研究員の眼で紹介してきたように、「時間や空間の無限」を指している場合もあれば、「無限集合」を指している場合もある。
今回は、「数列の無限」に関連して、無限大(∞)に関する話題について紹介したい。
今回は、「数列の無限」に関連して、無限大(∞)に関する話題について紹介したい。
「∞」(無限大)を表す記号
「∞」(無限大記号)については、研究員の眼「数学記号の由来について(6)-無限大(∞)、比例(∝)、相似(∽)等-」(2020.8.7)において、その使用及び由来について紹介した。そこで、述べたように、「無限大(infinity又はunlimited)」という概念は、今や世の中に一定程度知られた概念になっている。ただし、その概念は直感的にはそれなりに理解できるものになっていると思われるが、その数学的な定義はなかなか難しいものと思われる。
「無限大」というのは、「どの実数よりも大きな数」という形で捉えられていると思われるが、特定の数を表しているわけではなく、「いかなる数よりも大きい状態」を表しているというのがより正確ということになる。従って、「∞」(無限大記号)というのは、「どの実数よりも大きな数を表す記号」ではなくて、こうした「いかなる数よりも大きくなるという状態を表す記号」ということになる。ただし、実際には、特定の数を表しているかのような(誤解されやすい)形で使用されているケースも多いものと思われる。
また、「無限大」といわれても、数値の大小関係において、プラス方向だけでなく、マイナス方向の場合もあると思われるが、この場合には正の無限大が「∞ (+∞)」で負の無限大が「−∞」と表されることになる。
ただし、何度も繰り返すが、これはあくまでも記号であって、数字ではない。数学では、以下のような形で使用され、順序数が果てしなく、無限に続くことを示す際に使用されている。
「無限大」というのは、「どの実数よりも大きな数」という形で捉えられていると思われるが、特定の数を表しているわけではなく、「いかなる数よりも大きい状態」を表しているというのがより正確ということになる。従って、「∞」(無限大記号)というのは、「どの実数よりも大きな数を表す記号」ではなくて、こうした「いかなる数よりも大きくなるという状態を表す記号」ということになる。ただし、実際には、特定の数を表しているかのような(誤解されやすい)形で使用されているケースも多いものと思われる。
また、「無限大」といわれても、数値の大小関係において、プラス方向だけでなく、マイナス方向の場合もあると思われるが、この場合には正の無限大が「∞ (+∞)」で負の無限大が「−∞」と表されることになる。
ただし、何度も繰り返すが、これはあくまでも記号であって、数字ではない。数学では、以下のような形で使用され、順序数が果てしなく、無限に続くことを示す際に使用されている。
∞に大小関係はない
∞は具体的な数字ではないので、仮に何らかの2つの∞が算式等の中で現れても、その2つの間に大小関係があるというわけではない。ましてや、上記で述べたように、通常我々が考えているような意味においての等号関係(∞=∞)というのも、普通は適切な表現ではなく、「∞」が現れる場合の「=」は上記のような意味合いを有していることになる。
数列
以下では、「数列」について考える。
数列{an}について、その数列anの値が、nが大きくなるにつれて、
(1) ある有限な実数aに近づいていく場合、「aに収束(converge)」するといい(この時のaを「極限(値)」という)、
(2) 限りなく大きくなる場合、「(正の)無限大に発散(diverge)」するといい、
(3) 限りなく小さくなる(0に近づくという意味ではない)場合、「(負の)無限大に発散」するといい、
(4) 有限な実数へ収束せず、正の無限大や負の無限大にも発散しない場合、「振動(oscillating)」するという。
(2)から(4)のケースを含めて「発散」するということもある。
以下では、(1)の数列を「a」、(2)の数列を「∞」、(3)の数列を「-∞」で表したりすることにする。
この定義から明らかなように、∞やaで表される数列は、一意ではなく無数に存在することになる。
なお、今回の研究員の眼では、あくまでも「無限数列」を対象にしており、無限数列を前から順番に加えていくことで得られる「無限級数」について述べているわけではない。「無限級数」については、次回の研究員の眼で紹介することにする。
数列{an}について、その数列anの値が、nが大きくなるにつれて、
(1) ある有限な実数aに近づいていく場合、「aに収束(converge)」するといい(この時のaを「極限(値)」という)、
(2) 限りなく大きくなる場合、「(正の)無限大に発散(diverge)」するといい、
(3) 限りなく小さくなる(0に近づくという意味ではない)場合、「(負の)無限大に発散」するといい、
(4) 有限な実数へ収束せず、正の無限大や負の無限大にも発散しない場合、「振動(oscillating)」するという。
(2)から(4)のケースを含めて「発散」するということもある。
以下では、(1)の数列を「a」、(2)の数列を「∞」、(3)の数列を「-∞」で表したりすることにする。
この定義から明らかなように、∞やaで表される数列は、一意ではなく無数に存在することになる。
なお、今回の研究員の眼では、あくまでも「無限数列」を対象にしており、無限数列を前から順番に加えていくことで得られる「無限級数」について述べているわけではない。「無限級数」については、次回の研究員の眼で紹介することにする。
数列の和、差、積、商
「数列の和、差、積、商」については、以下のように定義される。
2つの数列{an}及び{bn}が与えられた時に、
(1) 和 {an+bn} 即ち、第n項のそれぞれの数の和の数列
(2) 差 {an-bn} 即ち、第n項のそれぞれの数の差の数列
(3) 積 {an×bn} 即ち、第n項のそれぞれの数の積の数列
(4) 商 {an÷bn} 即ち、第n項のそれぞれの数の商の数列
即ち、「数列の和、差、積、商」については、各々の数列の各項通しの「和、差、積、商」の結果として得られるものとして定義されることになる。
2つの数列{an}及び{bn}が与えられた時に、
(1) 和 {an+bn} 即ち、第n項のそれぞれの数の和の数列
(2) 差 {an-bn} 即ち、第n項のそれぞれの数の差の数列
(3) 積 {an×bn} 即ち、第n項のそれぞれの数の積の数列
(4) 商 {an÷bn} 即ち、第n項のそれぞれの数の商の数列
即ち、「数列の和、差、積、商」については、各々の数列の各項通しの「和、差、積、商」の結果として得られるものとして定義されることになる。
∞の和(足し算)
まずは、∞を含む足し算を考える。
{an}を有限な実数aに収束する数列とすると、∞に発散する数列に、どのような有限な実数aに収束する数列を足して(あるいは引いて)も、それは∞となる。このことは、一般的な感覚として理解できるだろう。即ち、この時、「=」を用いて、以下の通りに表すことにする。ここでの「=」は、あくまでも算式の両辺がともに∞(正の無限大)に発散するという意味合いで使用されていることになる。
∞+a=a+∞=∞
同様に、
∞+∞=∞
となり、これは「無限大に発散する数列に、無限大に発散する数列を加えてできる数列は、無限大に発散する」ということを表している。∞+(-∞)については、次の「∞-∞」で考える。
{an}を有限な実数aに収束する数列とすると、∞に発散する数列に、どのような有限な実数aに収束する数列を足して(あるいは引いて)も、それは∞となる。このことは、一般的な感覚として理解できるだろう。即ち、この時、「=」を用いて、以下の通りに表すことにする。ここでの「=」は、あくまでも算式の両辺がともに∞(正の無限大)に発散するという意味合いで使用されていることになる。
∞+a=a+∞=∞
同様に、
∞+∞=∞
となり、これは「無限大に発散する数列に、無限大に発散する数列を加えてできる数列は、無限大に発散する」ということを表している。∞+(-∞)については、次の「∞-∞」で考える。
∞の差(引き算)
次に、∞を含む引き算を考える。
aを有限な実数とすれば、以下の通りとなる。
∞-a=∞
a-∞=-∞
次に、「∞-∞」を考える。具体的な数列で見てみると、以下の通りとなる。
・{2n}(即ち、偶数の数列)と{n}(即ち、自然数列)の差は{n}となり、これは∞となる。
・{n}(即ち、偶数の数列)と{2n}(即ち、自然数列)の差は{-n}となり、これは-∞となる。
・{n}(即ち、偶数の数列)と{n}(即ち、自然数列)の差は{0}となり、これは0となる。
・{2n}(即ち、偶数の数列)と{2n-1}(即ち、奇数の数列)の差は{1}となり、これは1となる。
・{2n}(即ち、偶数の数列)と{2n-a}(aは任意の実数)の差は{a}となり、これはaとなる。
・{n}(即ち、偶数の数列)と{2nと(2n-1)が交互に現れる数列}(偶数と奇数が交互に現れる数列)の差は{1と―1が交互に現れる数列}となり、これは振動列となる。
このように、「∞-∞」は、∞にも-∞にも、あるいは任意の実数aにもなりえ、さらには「1」と「-1」が交互に現れる数列となり、収束も発散もしないで、振動することにもなる。
このような時、「∞-∞」を考えるのは「無意味」ということになるが、これを「不定(ふてい)」というような言い方をする。まさに「定まらない」という意味だが、「解が無数に存在する」ことを意味している。
aを有限な実数とすれば、以下の通りとなる。
∞-a=∞
a-∞=-∞
次に、「∞-∞」を考える。具体的な数列で見てみると、以下の通りとなる。
・{2n}(即ち、偶数の数列)と{n}(即ち、自然数列)の差は{n}となり、これは∞となる。
・{n}(即ち、偶数の数列)と{2n}(即ち、自然数列)の差は{-n}となり、これは-∞となる。
・{n}(即ち、偶数の数列)と{n}(即ち、自然数列)の差は{0}となり、これは0となる。
・{2n}(即ち、偶数の数列)と{2n-1}(即ち、奇数の数列)の差は{1}となり、これは1となる。
・{2n}(即ち、偶数の数列)と{2n-a}(aは任意の実数)の差は{a}となり、これはaとなる。
・{n}(即ち、偶数の数列)と{2nと(2n-1)が交互に現れる数列}(偶数と奇数が交互に現れる数列)の差は{1と―1が交互に現れる数列}となり、これは振動列となる。
このように、「∞-∞」は、∞にも-∞にも、あるいは任意の実数aにもなりえ、さらには「1」と「-1」が交互に現れる数列となり、収束も発散もしないで、振動することにもなる。
このような時、「∞-∞」を考えるのは「無意味」ということになるが、これを「不定(ふてい)」というような言い方をする。まさに「定まらない」という意味だが、「解が無数に存在する」ことを意味している。
∞の積(掛け算)
次に、∞を含む積を考える。
まずは、「∞×a」(a≠0)を考えると、
∞×a=∞(a>0)
∞×a=-∞(a<0)
となる。また、
次に、「∞×0」を考える。具体的な数列で見てみると、以下の通りとなる。
ここで、敢えて繰り返して述べておくが、「0」というのは、数字の0を表しているのではなくて、「0に収束する数列」を表している。
・{n2}と{1/n}の積は{n}となり、これは∞となる。
・{n2}と{-1/n}の積は{-n}となり、これは-∞となる。
・{n}と{1/n2}の積は{1/n}となり、これは0となる。
・{n}と{1/n}の積は{1}となり、これは1となる。
・{n}と{a/n}(aは任意の実数)の積は{a}となり、これはaとなる。
このように、「∞×0」は、∞にも-∞にも、あるいは任意の実数aにもなりうることになり、「不定」ということになる。
最後に、「∞×∞」については、その定義から∞になる。
まずは、「∞×a」(a≠0)を考えると、
∞×a=∞(a>0)
∞×a=-∞(a<0)
となる。また、
次に、「∞×0」を考える。具体的な数列で見てみると、以下の通りとなる。
ここで、敢えて繰り返して述べておくが、「0」というのは、数字の0を表しているのではなくて、「0に収束する数列」を表している。
・{n2}と{1/n}の積は{n}となり、これは∞となる。
・{n2}と{-1/n}の積は{-n}となり、これは-∞となる。
・{n}と{1/n2}の積は{1/n}となり、これは0となる。
・{n}と{1/n}の積は{1}となり、これは1となる。
・{n}と{a/n}(aは任意の実数)の積は{a}となり、これはaとなる。
このように、「∞×0」は、∞にも-∞にも、あるいは任意の実数aにもなりうることになり、「不定」ということになる。
最後に、「∞×∞」については、その定義から∞になる。
∞の商(割り算)
次に、∞を含む商を考える。
まずは、「∞÷a」を考えると、
∞÷a=∞(a>0)
∞÷a=-∞(a<0)
∞÷0 は無意味
となる。また、
a÷∞=0
次に、「∞÷∞」を考える。具体的な数列で見てみると、以下の通りとなる。
・{n2}と{n}の商は{n}となり、これは∞となる。
・{n}と{n2}の商は{1/n}となり、これは0となる。
・{n}と{n}の商は{1}となり、これは1となる。
・{n}と{n/a}(aは任意の実数)の商は{a}となり、これはaとなる。
このように、「∞÷∞」は、∞にも、あるいは任意の実数aにもなりうることになり、「不定」ということになる。
なお、2つの無限大に発散する数列について、その商の数列が、∞、有限な実数a(≠0)、0となる場合、それぞれ、分子となる数列は分母となる数列に比べて、「より高位の無限大」、「同位の無限大」、「より低位の無限大」というような言い方をする。
まずは、「∞÷a」を考えると、
∞÷a=∞(a>0)
∞÷a=-∞(a<0)
∞÷0 は無意味
となる。また、
a÷∞=0
次に、「∞÷∞」を考える。具体的な数列で見てみると、以下の通りとなる。
・{n2}と{n}の商は{n}となり、これは∞となる。
・{n}と{n2}の商は{1/n}となり、これは0となる。
・{n}と{n}の商は{1}となり、これは1となる。
・{n}と{n/a}(aは任意の実数)の商は{a}となり、これはaとなる。
このように、「∞÷∞」は、∞にも、あるいは任意の実数aにもなりうることになり、「不定」ということになる。
なお、2つの無限大に発散する数列について、その商の数列が、∞、有限な実数a(≠0)、0となる場合、それぞれ、分子となる数列は分母となる数列に比べて、「より高位の無限大」、「同位の無限大」、「より低位の無限大」というような言い方をする。
通常の数と数列の和、差、積、商の関係
「数列の和、差、積、商」について、数列が有限な値に収束する場合には、それは「通常の和、差、積、商」と同じことになる。あくまでも、∞が出てくる場合には、それが数列を対象にした式ということになる。
これまでに∞を含む算式を示してきたが、これはあくまでも、「数列の和、差、積、商」の関係の示すために簡潔な表現として認められるものである。いわゆる数の四則演算とは異なるものであることは、改めて述べておきたい。
∞はあくまでも記号であって数字ではなく、数を対象にした演算の対象にはならないものである。
これまでに∞を含む算式を示してきたが、これはあくまでも、「数列の和、差、積、商」の関係の示すために簡潔な表現として認められるものである。いわゆる数の四則演算とは異なるものであることは、改めて述べておきたい。
∞はあくまでも記号であって数字ではなく、数を対象にした演算の対象にはならないものである。
最後に
今回は、無限大(∞)に関する話題について紹介してきた。
日常生活では全く関係のないものであるが、何らかの機会に一応気にかけてもらえればと思って、紹介させていただいた次第である。
日常生活では全く関係のないものであるが、何らかの機会に一応気にかけてもらえればと思って、紹介させていただいた次第である。
(2022年10月21日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
新着記事
-
2025年11月04日
今週のレポート・コラムまとめ【10/28-10/31発行分】 -
2025年10月31日
交流を広げるだけでは届かない-関係人口・二地域居住に求められる「心の安全・安心」と今後の道筋 -
2025年10月31日
ECB政策理事会-3会合連続となる全会一致の据え置き決定 -
2025年10月31日
2025年7-9月期の実質GDP~前期比▲0.7%(年率▲2.7%)を予測~ -
2025年10月31日
保険型投資商品の特徴を理解すること(欧州)-欧州保険協会の解説文書
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【無限について(その5)-無限大(∞)について-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
無限について(その5)-無限大(∞)について-のレポート Topへ


















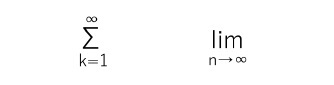

 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




