じゃんけんの拡張－“下剋上”のある、じゃんけんはいかが?

保険研究部主席研究員兼気候変動リサーチセンターチーフ気候変動アナリスト兼ヘルスケアリサーチセンター主席研究員篠原拓也

このレポートの関連カテゴリ

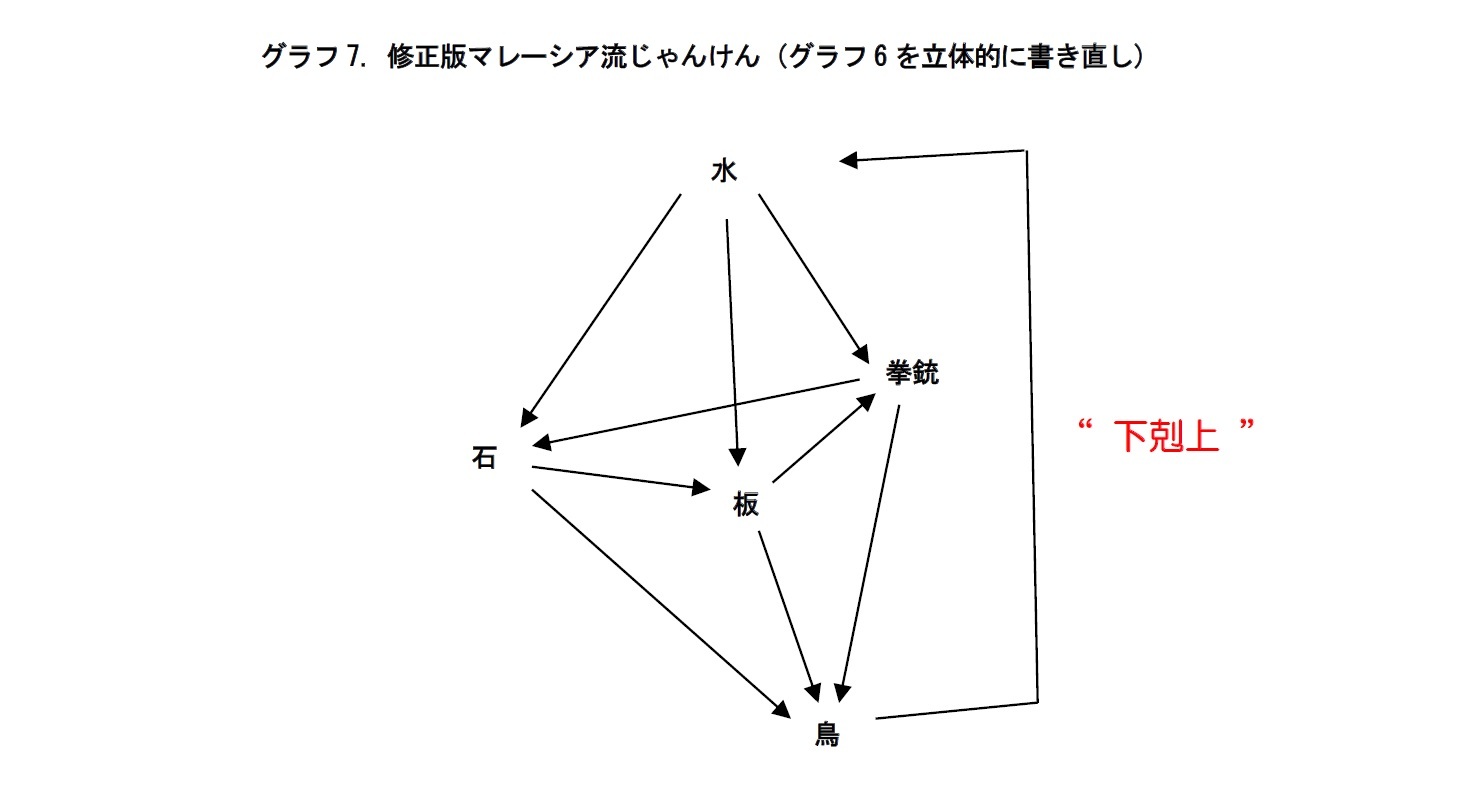
◇ 修正版マレーシア流じゃんけんには、“下剋上”が組み込まれている

このじゃんけんでは、水と鳥が味わい深い。水は、石と板と拳銃のどれにも勝てる強い手だ。対照的に、鳥は、石と板と拳銃のどれにも負けてしまう弱い手だ。しかし、弱い鳥が、強い水に勝つというルールを設けたことで、一種の“下剋上”の要素が組み込まれた格好になっている。このことは、次のように、グラフを立体的に書き直してみるとよくわかる。(グラフ6とグラフ7は同じ内容)

石、板、拳銃の3つの手は、通常のじゃんけんのグー、チョキ、パーの三すくみと同じ関係だ。各プレーヤーは、通常のじゃんけんのつもりで、石、板、拳銃を出すことができる。

そして、この3つのどれにも勝てる、水という強い手がある。「相手は通常のじゃんけんのつもりで石、板、拳銃のどれかを出してくるだろう」と読めたら、水を出せば勝てる。

ところが、板、石、拳銃のどれにも負けてしまう弱い手である鳥が、水にだけは勝てる。「相手が水を出してくる」と読んだら、ここぞとばかりに鳥を出して、“下剋上”を狙うことができるわけだ。

このように、相手の心理を踏まえて手を出す奥深さが、修正版マレーシア流じゃんけんの醍醐味といえる。

◇ じゃんけんで盛り上がってみるのもよいかも

じゃんけんは、何の道具も要らず、いつでもどこでもできる遊びだ。通常のじゃんけんだけではなく、5つの手を使った「下剋上」の要素を組み込んだものも考えられる。

さらに、出せる手の数を6つ、7つ、…と増やした、新種じゃんけんを考えてみるのもよいだろう。ただし、出せる手の数を増やせば、それぞれの手の間の勝ち負けの関係も増えてしまうため、複雑さが増してしまう点は覚悟しないといけない。

最近、コロナ禍の影響で、リアルの宴会はめっきり減った。だが、じゃんけんは、オンラインでもできる。オンラインの宴会などで、こうしたじゃんけんで盛り上がってみるのもよいように思うが、いかがだろうか。

(参考文献)

「狐拳」「虫拳」(フリー百科事典『ウィキペディア（Wikipedia）』)

「国によって違う！世界のジャンケンの話：キャスト」(何ゴト? 何かと気になる事が書いてあるブログ, 2019.3.18)

「一般化ジャンケン」伊藤大雄(「オペレーションズ・リサーチ」(公益社団法人日本オペレーションズ・リサーチ学会) , pp156-160, Vol.58 No.3 (2013年3月号))

(付録1) 「4つの手を使って行うじゃんけんには、必ず無意味な手がある」ことの説明

ある1つの手が、他の3つの手すべてに勝つような場合、他の3つの手は、いずれも無意味な手となる。(というか、そもそも、じゃんけんとして成立しなくなる。)

逆に、ある1つの手が、他の3つの手すべてに負けるような場合、この手は、無意味な手となる。

したがって、4つの手は、それぞれ他の手に対して、全勝したり、全敗したりすることはない。

ここで、4つの手を a、b、c、d としよう。そして、「aはbに勝つ」を「a>b」、「aはbに負ける」を「a<b」と表そう。

aはb、c、dに対して全勝したり、全敗したりしない。そこで、a>b、a>c、a<dとしよう。

そして、bとcの間の勝ち負けを、b>cと置いてみよう。

すると、cはaにもbにも負けているので、全敗しないためには、dに勝つ必要がある。つまり、c>dとなる。

ここで、少し振り返ってみると、aとその他の手の勝ち負けの関係、cとその他の手の勝ち負けの関係はすべて決している。まだ、決まっていないのは、bとdの勝ち負けの関係だけとなる。

b>dとしてみよう。このとき、bとcはいずれも、aに負けて、dに勝つ。そして、bはcに勝つ。したがって、どのようなケースでも、cを出す代わりに、bを出したほうがよいことになる。つまり、cは無意味な手となる。

b<dとしたらどうか。このとき、aとbはいずれも、dに負けて、cに勝つ。そして、aはbに勝つ。したがって、どのようなケースでも、bを出す代わりに、aを出したほうがよいことになる。つまり、bは無意味な手となる。

bとcの間の勝ち負けを、b<cと置いて話を進めた場合も、同様の展開となる。このように、4つの手を使って行うじゃんけんでは、いずれの場合も、無意味な手ができることとなる。

(付録2)「5つの手で行うじゃんけんのうち、無意味な手がないものは、トカゲスポックじゃんけんと、修正版マレーシア流じゃんけんの、2つのグラフの形しかない」ことの説明

ある1つの手が、他の4つの手すべてに勝つような場合、他の4つの手は、いずれも無意味な手となる。((付録1)の最初に述べたのと同様に、そもそも、じゃんけんとして成立しなくなる。)

逆に、ある1つの手が、他の4つの手すべてに負けるような場合、この手は、無意味な手となる。

したがって、5つの手は、それぞれ他の手に対して、全勝したり、全敗したりすることはない。5つの手は、他の手に対して、3勝1敗か、2勝2敗か、1勝3敗か、のいずれかとなる。

5つの手のうち、2勝2敗となる手がいくつありうるか、考えてみよう。

5つの手すべてが2勝2敗となるケースが、トカゲスポックじゃんけんとなる。また、5つの手のうち、3つが2勝2敗となるケースが、修正版マレーシア流じゃんけんとなる。

2勝2敗となる手の数が、4つや、2つや、ゼロ(なし)個といった、偶数個になることはありえない。なぜかというと、3勝1敗や、1勝3敗となる残りの手の数が、奇数個となり、5つの手からなる異なる手同士の勝ち負けの組み合わせ(全部で10通り)で、勝ちの数の合計と、負けの数の合計が合わなくなってしまうからだ。

したがって、トカゲスポックじゃんけんと、修正版マレーシア流じゃんけん以外で、無意味な手がないじゃんけんの可能性があるのは、5つの手のうち、1つの手が2勝2敗で、残り4つの手のうち、2つの手が3勝1敗、2つの手が1勝3敗、というケースだけとなる。

ここで、5つの手を a、b、c、d、e としよう。(付録1)と同じように、勝ち負けの関係を「a>b」、「a<b」などと表すことにしよう。

aが2勝2敗、bとcが3勝1敗、dとeが1勝3敗としよう。

そして、bとcの勝ち負けを b>c、dとeの勝ち負けを d>e と置こう。

すると、cは3勝1敗なので、b以外にはすべて勝つ。つまり、c>a、c>d、c>eとなる。

一方、dは1勝3敗なので、e以外にはすべて負ける。つまり、d<a、d<b、d<cとなる。

ここで、cとdはいずれも、bに負けて、eに勝つ。aに対しては、cはaに勝ち、dはaに負ける。そして、cはdに勝つ。したがって、どのようなケースでも、dを出す代わりに、cを出したほうがよいことになる。つまり、dは無意味な手となる。

bとcの勝ち負けをb<cと置いたり、dとeの勝ち負けを d<eと置いたりして話を進めた場合も、同様の展開となる。つまり、5つの手のうち、1つの手が2勝2敗で、残り4つの手のうち、2つの手が3勝1敗、2つの手が1勝3敗、というケースでは、無意味な手ができてしまう。

したがって、5つの手で行うじゃんけんのうち、無意味な手がないものは、トカゲスポックじゃんけんと、修正版マレーシア流じゃんけんの、2つのグラフの形しかない、こととなる。

日付	タイトル	執筆者	媒体
2025/04/22	審査の差の定量化－審査のブレはどれくらい?	篠原拓也	研究員の眼
2025/04/15	患者数:入院は減少、外来は増加－2023年の「患者調査」にコロナ禍の影響はどうあらわれたか?	篠原拓也	基礎研レター
2025/04/08	センチネル効果の活用－監視されていると行動が改善する?	篠原拓也	研究員の眼
2025/04/01	1, 2, 4, 8, 16, ○, …－思い込みには要注意！	篠原拓也	研究員の眼

日付

タイトル

執筆者

媒体

2025/04/22

審査の差の定量化－審査のブレはどれくらい?

篠原拓也

研究員の眼

2025/04/15

患者数:入院は減少、外来は増加－2023年の「患者調査」にコロナ禍の影響はどうあらわれたか?

篠原拓也

基礎研レター