- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 「三角関数」と「フーリエ変換」-三角関数の幅広い実社会利用での基礎となる重要な数学的手法-
コラム
2021年11月10日
文字サイズ
- 小
- 中
- 大
フーリエ変換
スペクトル
「スペクトル(spectrum)」というのは、一般的に「複雑な情報や信号をその成分に分解し、成分ごとの大小に従って配列したもの」をいう。光や音や電磁波信号は様々な周波数の成分から構成されているが、そのようなものから周波数毎の強さを定量的に求める処理を「スペクトル解析(spectrum analysis)」という。
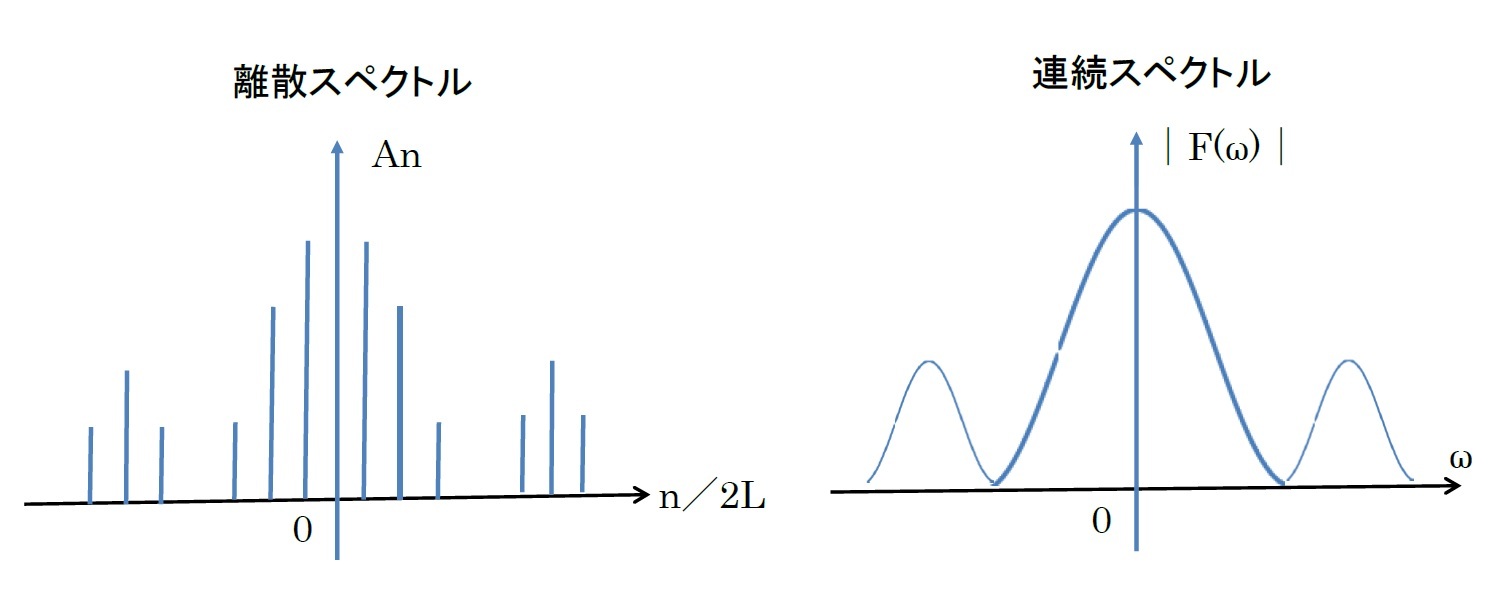
周期関数に対しては、フーリエ級数展開により、周波数毎のフーリエ係数に基づく振幅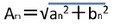 の値を縦軸にプロットすることで、「離散スペクトル」が得られる。また、無限に長い周期を持つ、結果として周期関数とは限らない関数に対しては、「フーリエ変換」により、フーリエ係数が周波数に対して連続的に得られ、これらの|F(ω)|を縦軸にプロットしたものとして、「連続スペクトル」が得られる。
の値を縦軸にプロットすることで、「離散スペクトル」が得られる。また、無限に長い周期を持つ、結果として周期関数とは限らない関数に対しては、「フーリエ変換」により、フーリエ係数が周波数に対して連続的に得られ、これらの|F(ω)|を縦軸にプロットしたものとして、「連続スペクトル」が得られる。
周期関数に対しては、フーリエ級数展開により、周波数毎のフーリエ係数に基づく振幅
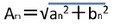 の値を縦軸にプロットすることで、「離散スペクトル」が得られる。また、無限に長い周期を持つ、結果として周期関数とは限らない関数に対しては、「フーリエ変換」により、フーリエ係数が周波数に対して連続的に得られ、これらの|F(ω)|を縦軸にプロットしたものとして、「連続スペクトル」が得られる。
の値を縦軸にプロットすることで、「離散スペクトル」が得られる。また、無限に長い周期を持つ、結果として周期関数とは限らない関数に対しては、「フーリエ変換」により、フーリエ係数が周波数に対して連続的に得られ、これらの|F(ω)|を縦軸にプロットしたものとして、「連続スペクトル」が得られる。
フーリエ変換は関数の表現の一種であり、時間の関数だったものを周波数の関数に変換したものと言え、これを「周波数領域表現」と呼んでいる。すなわち、フーリエ変換は、時間領域表現を周波数領域表現に変換するものとなる。時間領域で適用可能な線形操作(例えば2つの波形を重ね合わせる)は、周波数領域でも容易に行えることになる。
フーリエ級数とフーリエ変換の関係
これまで述べてきたように、「フーリエ級数展開」により、周期関数に対して、ある領域内にある波形を基本周波数の整数倍の振動で表現した時の、各周波数成分の係数としての「フーリエ係数」が得られることになる。
これに対して、無限に長い周期を持つ、結果として周期関数とは限らない関数を考えると、「フーリエ変換」により、フーリエ係数は周波数に対して連続的に得られ、この場合の関数は、無限級数ではなく、「フーリエ逆変換」として、積分で表されることになる。
即ち、周期関数を様々な正弦波の組み合わせとして表現することが「フーリエ級数展開」であり、無限に長い周期を有する関数を連続スペクトルに変換するのが「フーリエ変換」ということになる。なお、フーリエ変換の一種に「離散フーリエ変換」があり、この場合、離散的な関数から「離散スペクトル」が得られる。
これに対して、無限に長い周期を持つ、結果として周期関数とは限らない関数を考えると、「フーリエ変換」により、フーリエ係数は周波数に対して連続的に得られ、この場合の関数は、無限級数ではなく、「フーリエ逆変換」として、積分で表されることになる。
即ち、周期関数を様々な正弦波の組み合わせとして表現することが「フーリエ級数展開」であり、無限に長い周期を有する関数を連続スペクトルに変換するのが「フーリエ変換」ということになる。なお、フーリエ変換の一種に「離散フーリエ変換」があり、この場合、離散的な関数から「離散スペクトル」が得られる。
ジョゼフ・フーリエとは
さて、ここで、フーリエ変換の名で知られる「ジョセフ・フーリエ(Joseph Fourier)」について簡単に紹介しておく。ジョセフ・フーリエは、フランス革命の時代に活躍したフランスの数学者・物理学者で、固体内での熱伝導に関する研究から「熱伝導方程式(フーリエの方程式)」を導き、これを解くためにフーリエ解析と呼ばれる理論を展開した。
1798年にナポレオンがエジプト遠征を行ったときに、フーリエも文化使節団の一員として随行しており、この時に「熱」に興味を有したようだ。
フーリエは、1824年には、地球の大きさと太陽との距離に基づいて、地球の気温を算定し、地球の気温は本来的にはより低いはずだ、との結論から、いわゆる「温室効果(greenhouse effect)」3を発見している。
3 大気圏の存在により、地球の表面から発せられる放射が、大気圏外に届く前にその一部が大気中の物質に吸収されることで、そのエネルギーが大気圏より内側に滞留する結果として、大気圏内部の気温が上昇する現象
1798年にナポレオンがエジプト遠征を行ったときに、フーリエも文化使節団の一員として随行しており、この時に「熱」に興味を有したようだ。
フーリエは、1824年には、地球の大きさと太陽との距離に基づいて、地球の気温を算定し、地球の気温は本来的にはより低いはずだ、との結論から、いわゆる「温室効果(greenhouse effect)」3を発見している。
3 大気圏の存在により、地球の表面から発せられる放射が、大気圏外に届く前にその一部が大気中の物質に吸収されることで、そのエネルギーが大気圏より内側に滞留する結果として、大気圏内部の気温が上昇する現象
フーリエ解析とその応用
上記で述べたように、フーリエによる最初の動機は熱伝導方程式を解くことであった。ただし、フーリエが考え出したテクニックから発展してきた、フーリエ級数やフーリエ変換(以下、フーリエ逆変換を含む)に代表される「フーリエ解析4」は、複雑な関数を周波数成分に分解してより簡単に記述することを可能にすることから、電気工学、振動工学、音響学、光学、信号処理、量子力学などの現代科学の幅広い分野、さらには経済学等にも応用されてきている。
具体的に、いくつかの例を挙げると、以下の通りである。
まずは、前回の研究員の眼で説明したように、「音声処理」においては、音声信号を送信する場合に、変調という仕組みで音声信号を表現して送信するが、受信機でこれらの電波を音声信号に変える時、また、雑音を消すための「ノイズ除去」において、フーリエ解析が使用される。
さらに、画像等のデジタルデータの「圧縮技術」にもフーリエ解析が使用される。
また、「微分方程式」というのは、各種の要素(変数)の結果として定まる関数Fの微分係数(変化率)dF/dtの間の関係式を示すものであるが、多くの世の中の現象(波動や熱伝導等)が微分方程式5で表現される。この微分方程式を解いて、Fを求めることによって、こうした現象を解明することができることになる。フーリエ級数展開やフーリエ変換は、これらの微分方程式を解く上で、重要な役割を果たしている。例えば、物理学で現れるような微分方程式では、フーリエ級数展開を用いることで、微分方程式を代数方程式(我々が一般的に見かける、多項式を等号で結んだ形で表される方程式)に変換することで単純化をすることができることになる。
医療の分野では、「CT(computed tomography:コンピューター断層撮影)」や「MRI(magnetic resonance imaging:核磁気共鳴画像法)」の画像データ処理において、フーリエ解析が使用される。
「サンプリング理論」として知られる、自然界にある連続したアナログ情報(信号)をコンピューターが扱えるデジタル情報(信号)に変換するときに、どの程度の間隔でサンプリングすればよいかを定量的に示す「サンプリング定理」等の基礎的な理論があるが、このサンプリング理論とフーリエ変換を用いることで、CT、MRIなどの画像処理がコンピューターで行われていくことになる。
なお、有名な「DNA(デオキシリボ核酸)の二重らせん構造」は、X線解析とフーリエ変換によって発見されているし、宇宙探査機が撮影する天体の画像等にも、フーリエ変換を用いた信号処理が使用されている。
4 「フーリエ変換」も万能ではなく、フーリエ変換が可能な関数の条件がある。そこで、「ラプラス変換」という手法も使用されるが、今回の研究員の眼のシリーズでは、ラプラス変換については説明しない。また、「フーリエ解析」における重要な手法である「離散フーリエ変換」や「高速フーリエ変換」についても触れていない。
5 変数が1つの微分方程式が「常微分方程式」であり、複数の変数で表されるのが「偏微分方程式」となる。代表的なものとして、波動方程式、熱伝導方程式、ラプラス方程式などが挙げられる。
具体的に、いくつかの例を挙げると、以下の通りである。
まずは、前回の研究員の眼で説明したように、「音声処理」においては、音声信号を送信する場合に、変調という仕組みで音声信号を表現して送信するが、受信機でこれらの電波を音声信号に変える時、また、雑音を消すための「ノイズ除去」において、フーリエ解析が使用される。
さらに、画像等のデジタルデータの「圧縮技術」にもフーリエ解析が使用される。
また、「微分方程式」というのは、各種の要素(変数)の結果として定まる関数Fの微分係数(変化率)dF/dtの間の関係式を示すものであるが、多くの世の中の現象(波動や熱伝導等)が微分方程式5で表現される。この微分方程式を解いて、Fを求めることによって、こうした現象を解明することができることになる。フーリエ級数展開やフーリエ変換は、これらの微分方程式を解く上で、重要な役割を果たしている。例えば、物理学で現れるような微分方程式では、フーリエ級数展開を用いることで、微分方程式を代数方程式(我々が一般的に見かける、多項式を等号で結んだ形で表される方程式)に変換することで単純化をすることができることになる。
医療の分野では、「CT(computed tomography:コンピューター断層撮影)」や「MRI(magnetic resonance imaging:核磁気共鳴画像法)」の画像データ処理において、フーリエ解析が使用される。
「サンプリング理論」として知られる、自然界にある連続したアナログ情報(信号)をコンピューターが扱えるデジタル情報(信号)に変換するときに、どの程度の間隔でサンプリングすればよいかを定量的に示す「サンプリング定理」等の基礎的な理論があるが、このサンプリング理論とフーリエ変換を用いることで、CT、MRIなどの画像処理がコンピューターで行われていくことになる。
なお、有名な「DNA(デオキシリボ核酸)の二重らせん構造」は、X線解析とフーリエ変換によって発見されているし、宇宙探査機が撮影する天体の画像等にも、フーリエ変換を用いた信号処理が使用されている。
4 「フーリエ変換」も万能ではなく、フーリエ変換が可能な関数の条件がある。そこで、「ラプラス変換」という手法も使用されるが、今回の研究員の眼のシリーズでは、ラプラス変換については説明しない。また、「フーリエ解析」における重要な手法である「離散フーリエ変換」や「高速フーリエ変換」についても触れていない。
5 変数が1つの微分方程式が「常微分方程式」であり、複数の変数で表されるのが「偏微分方程式」となる。代表的なものとして、波動方程式、熱伝導方程式、ラプラス方程式などが挙げられる。
まとめ
以上、今回は「フーリエ級数展開」と「フーリエ変換」について、簡単に紹介した。
今回の研究員の眼は、算式が多く、また結果を示すだけに留めているので、やや複雑になってしまったと思われる。
ただし、これにより、いかに三角関数が我々の日常生活と深い関わり合いがあり、三角関数が無くてはならないものであるかが、少しはご理解いただけたら、と思っている。
これまで述べてきたことは、こうした分野に関わっている方々にとっては常識的なことではあるが、一般の人々にとっては必ずしも認識されていないものであると思われる。
現代の先端的な技術の基礎に三角関数があり、社会にとって必要不可欠なツールとなっていることを是非ご認識いただければと思っている。
今回の研究員の眼は、算式が多く、また結果を示すだけに留めているので、やや複雑になってしまったと思われる。
ただし、これにより、いかに三角関数が我々の日常生活と深い関わり合いがあり、三角関数が無くてはならないものであるかが、少しはご理解いただけたら、と思っている。
これまで述べてきたことは、こうした分野に関わっている方々にとっては常識的なことではあるが、一般の人々にとっては必ずしも認識されていないものであると思われる。
現代の先端的な技術の基礎に三角関数があり、社会にとって必要不可欠なツールとなっていることを是非ご認識いただければと思っている。
(2021年11月10日「研究員の眼」)
関連レポート
- 「三角関数」って、何でしたっけ?-sin(サイン)、cos(コサイン)、tan(タンジェント)-
- 数学記号の由来について(7)-三角関数(sin、cos、tan等)-
- 数学記号の由来について(9)-数学定数(e、π、φ、i)-
- 数学記号の由来について(8)-「数」を表す記号-
- 「三角関数」の基本的な定理とその有用性を再確認してみませんか(その1)-正弦定理、余弦定理、正接定理-
- 「三角関数」の基本的な定理とその有用性を再確認してみませんか(その2)-加法定理、二倍角、三倍角、半角の公式等-
- 「三角関数」と「波」の関係-三角関数による「波」の表現と各種の波(電磁波、音波、地震波等)-
- 「三角関数」と「波」の関係(その2)-電波によるデータ送信の仕組みと三角関数による「波」の表現の利用-
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
新着記事
-
2025年10月29日
生活習慣病リスクを高める飲酒の現状と改善に向けた対策~男女の飲酒習慣の違いに着目して -
2025年10月29日
地域イベントの現実と課題-渋谷のハロウィンをイベントとして運営できるか- -
2025年10月28日
試練の5年に踏み出す中国(前編)-「第15次五カ年計画」の5年間は、どのような5年か -
2025年10月28日
地域医療連携推進法人の現状と今後を考える-「連携以上、統合未満」で協力する形態、その将来像は? -
2025年10月28日
東宝の自己株式取得-公開買付による取得
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【「三角関数」と「フーリエ変換」-三角関数の幅広い実社会利用での基礎となる重要な数学的手法-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
「三角関数」と「フーリエ変換」-三角関数の幅広い実社会利用での基礎となる重要な数学的手法-のレポート Topへ


















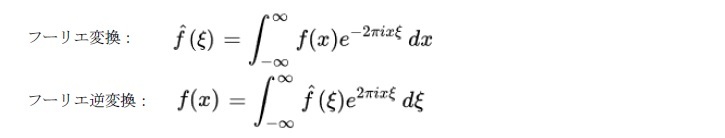
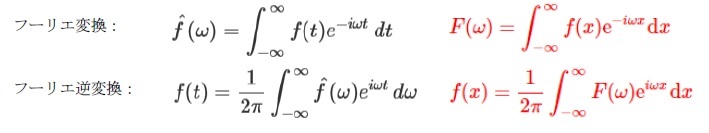

 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




