- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 「三角関数」と「波」の関係-三角関数による「波」の表現と各種の波(電磁波、音波、地震波等)-
コラム
2021年05月18日
文字サイズ
- 小
- 中
- 大
三角関数による「波」の表現
パターンが周期的である(周期性を有する)波動が一般的に取り扱われるが、このような場合、先の正弦曲線や余弦曲線といった三角関数のグラフをベースにして、これらにいくつかの要素を反映させたものを重ね合わせることで表すことができる。
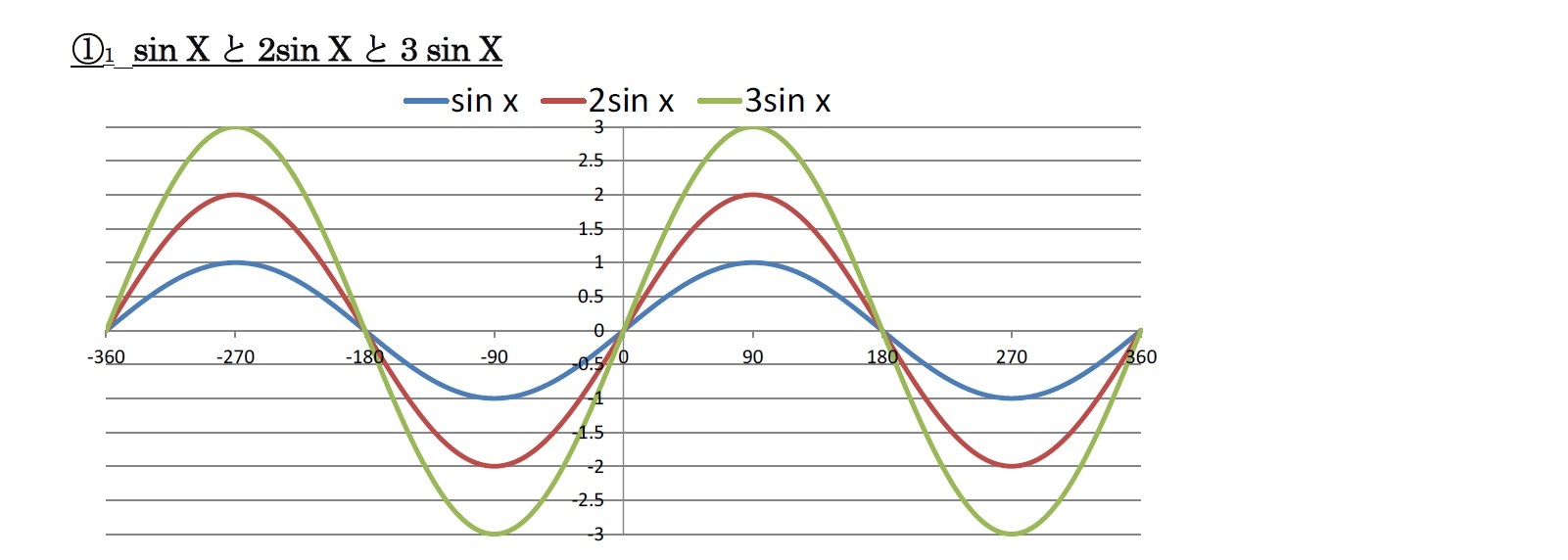
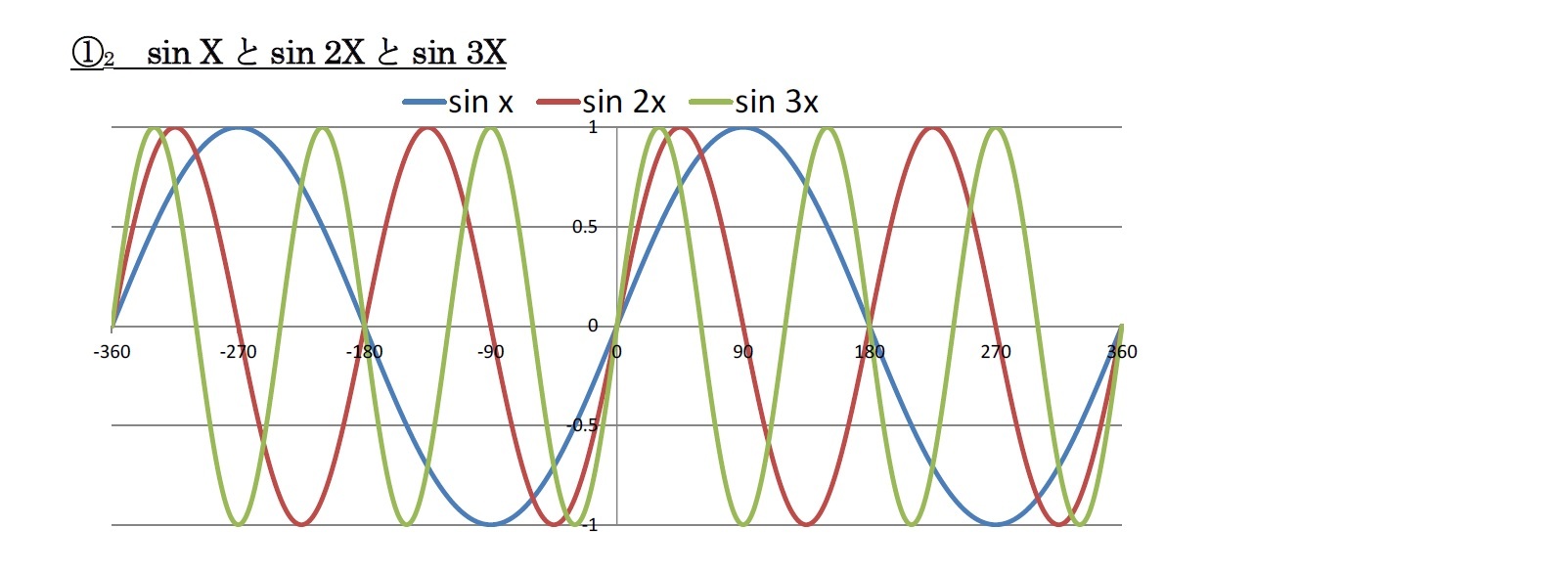
(1) y=a sin bx という関数を考えると、
・aが振幅を決定し、aが大きくなると振幅が大きくなる。
・bが波長を決定し、bが大きくなると波長が短くなる。
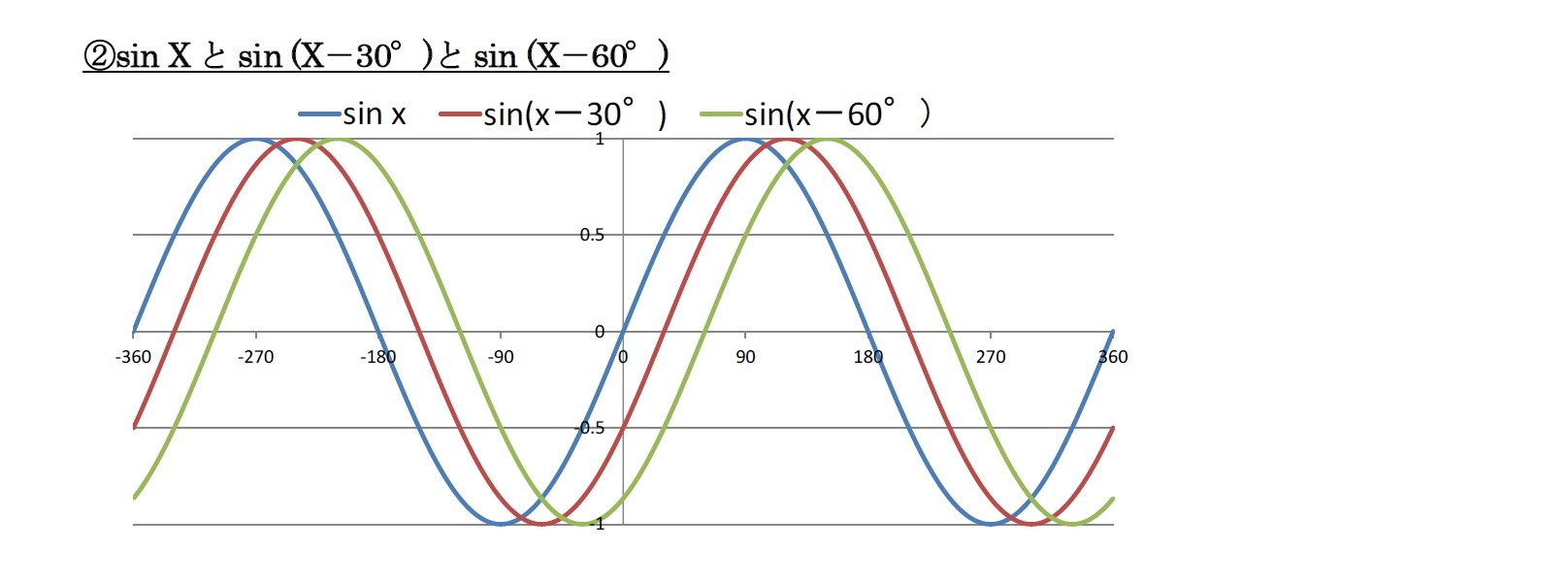
(2) y=sin(x±α) という関数を考えると、
・αだけ、x軸に左右にずれていくことになる。
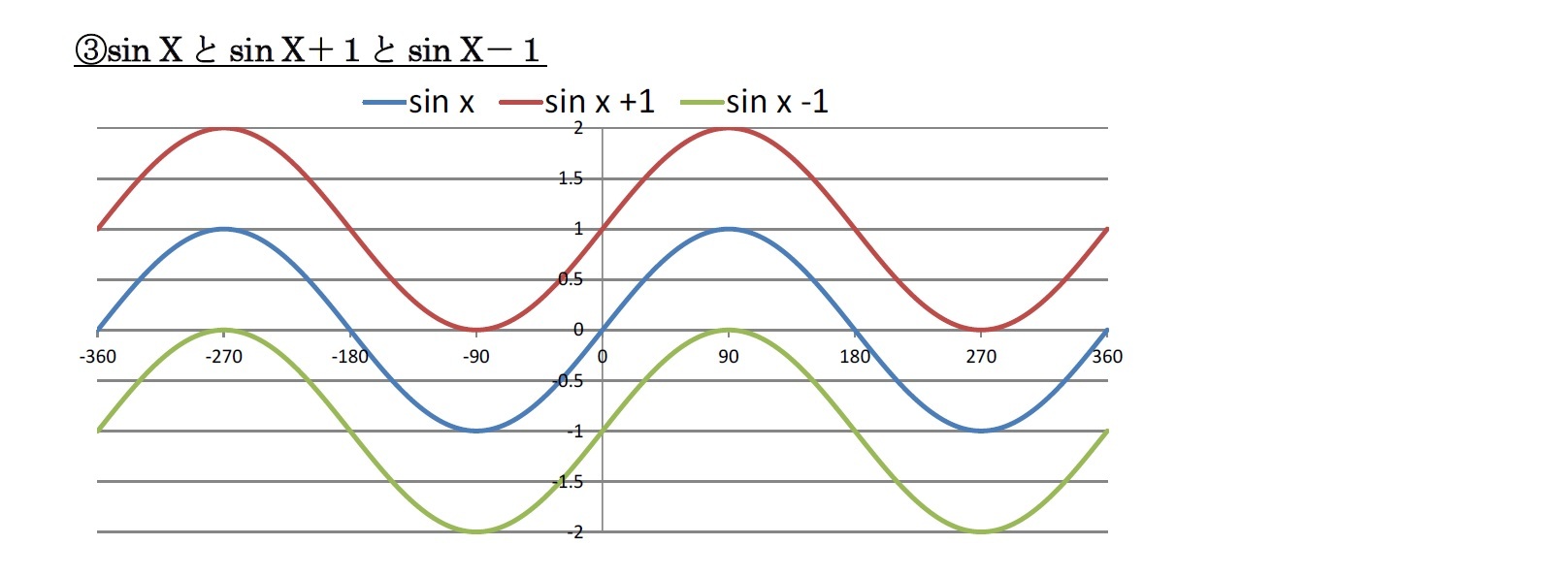
(3) y= sin x ±aという関数を考えると
・a だけ、上下変動することになる。
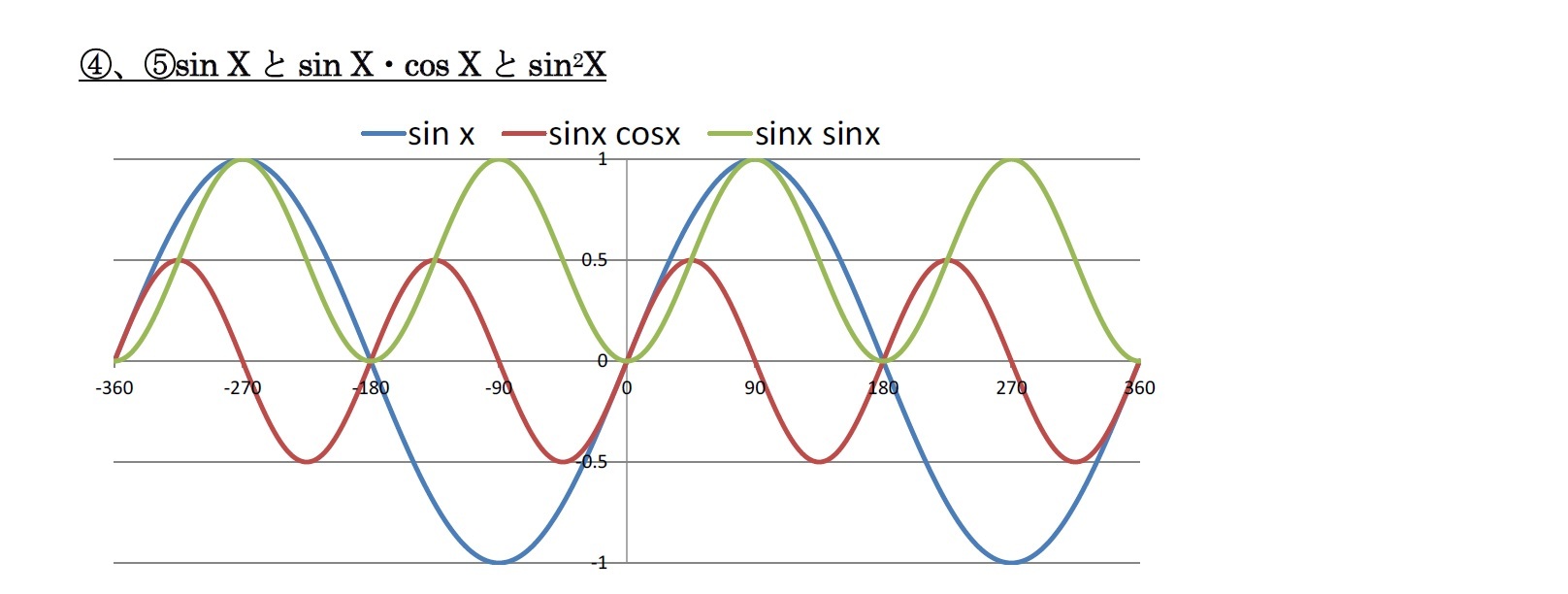
(4) y= sin x×cos x という関数を考えると、
・振幅と波長が半分の曲線となる。
(5) y= sin x×sin x(=sin2x) という関数を考えると、
・波長は同じで、振幅が半分で正の値のみをとる曲線となる。
(1) y=a sin bx という関数を考えると、
・aが振幅を決定し、aが大きくなると振幅が大きくなる。
・bが波長を決定し、bが大きくなると波長が短くなる。
(2) y=sin(x±α) という関数を考えると、
・αだけ、x軸に左右にずれていくことになる。
(3) y= sin x ±aという関数を考えると
・a だけ、上下変動することになる。
(4) y= sin x×cos x という関数を考えると、
・振幅と波長が半分の曲線となる。
(5) y= sin x×sin x(=sin2x) という関数を考えると、
・波長は同じで、振幅が半分で正の値のみをとる曲線となる。
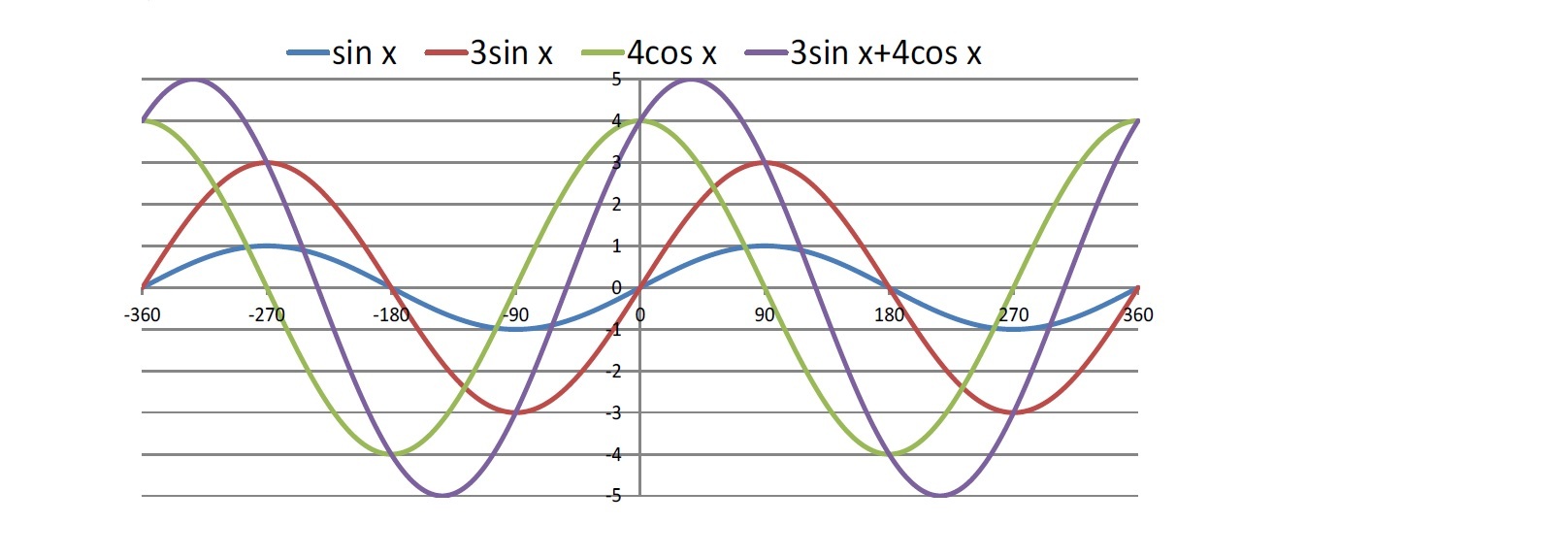
なお、前回の研究員の眼で紹介したように、三角関数の合成公式を用いると、
y=3sin x+4cos x=5sin (x+α)
ここで、αは、sinα=4/5 cosα=3/5 を満たす角度で、約53°となる。
これは、グラフでは以下のように示される。
y=3sin x+4cos x=5sin (x+α)
ここで、αは、sinα=4/5 cosα=3/5 を満たす角度で、約53°となる。
これは、グラフでは以下のように示される。
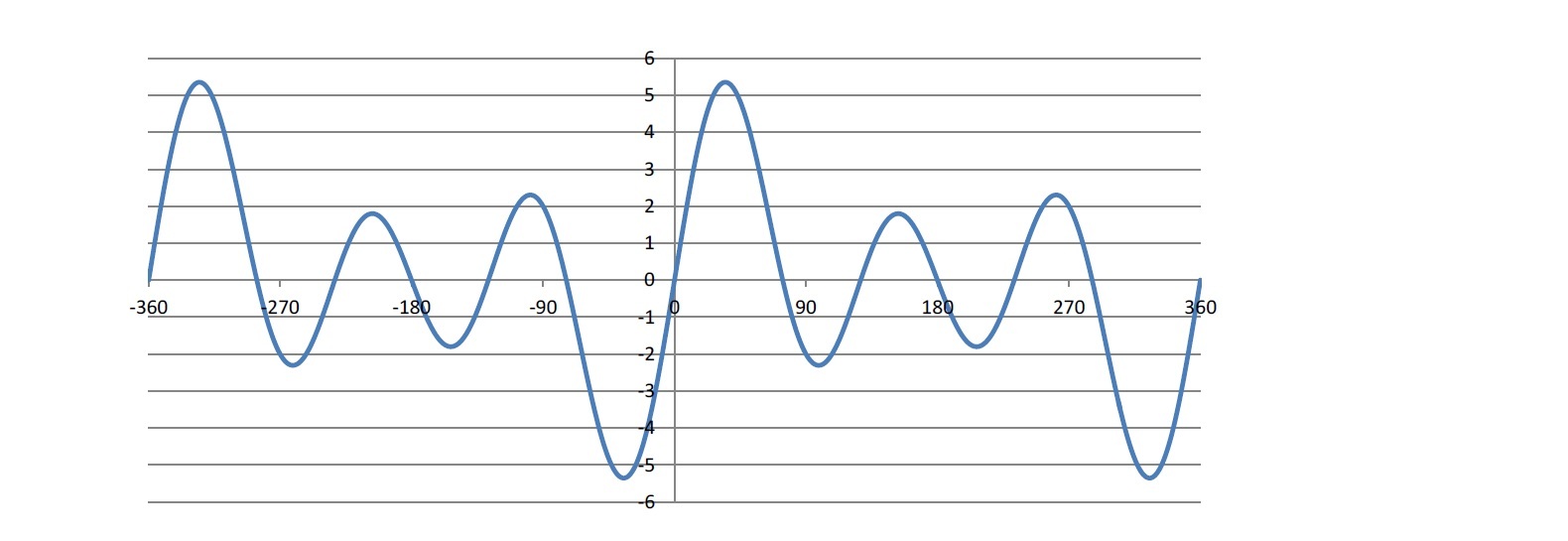
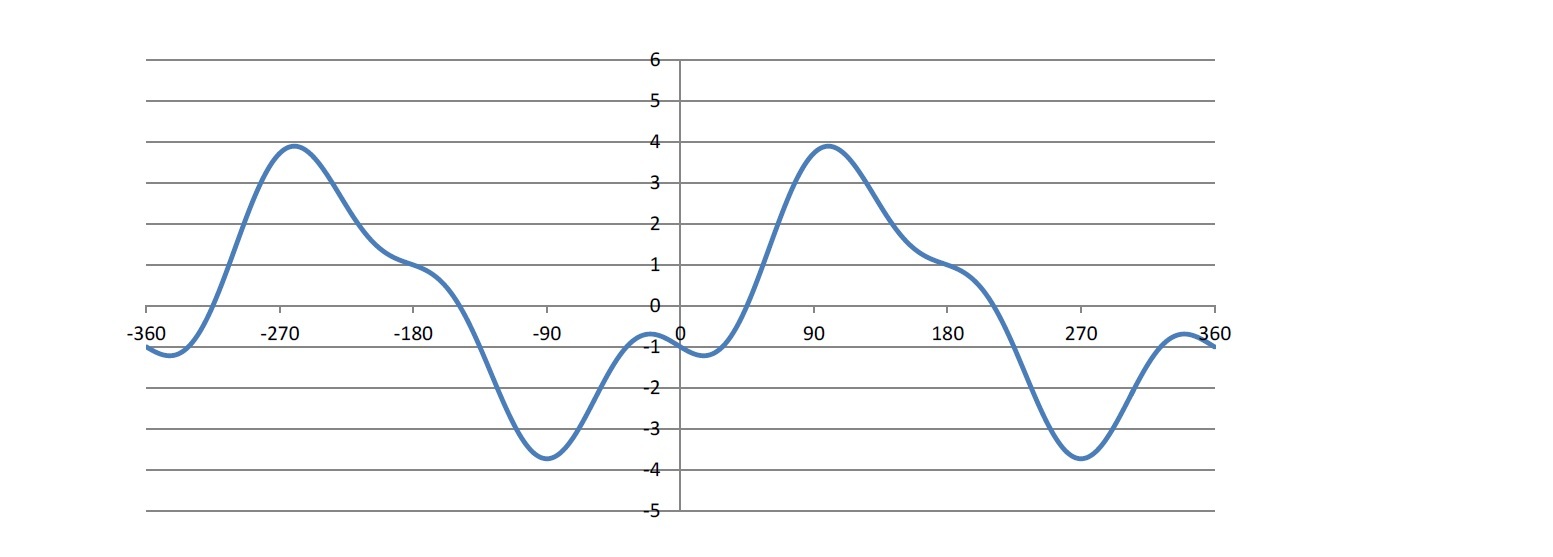
このようにいくつかの三角関数を組み合わせることで、複雑な波を表現できることになる。
まとめ
以上、今回は「三角関数」と「波」の関係について、紹介した。
三角関数をグラフで表すと波形となり、いくつかの三角関数を組み合わせることで、複雑な波を形作ることができることがわかったと思う。
それでは、今回簡単に紹介したような電磁波や音波や地震波といった波は、実際にはどのような波形をしていて、それらを本当に三角関数で表現することができるのだろうか。
これについては、例えば、一定の周期を有する「周期関数」については、基本的には(「区分的に滑らかな」という条件を満たす場合には)、どんなに複雑でも、単純な波動の数学的な表現である正弦関数や余弦関数で表現することができる、ことが知られている。さらには、周期関数ではない関数も、(「区分的に滑らかで、かつ連続で、かつ絶対可積分」という条件を満たす場合には)、同様に三角関数で表現することができる。ここで用いられるのが、複雑な波を単純な波へと分解することになる数学的手法である「フーリエ級数展開」であり、「フーリエ変換」と呼ばれるものである。
こうした数学的手法があるからこそ、複雑な電波や光波や音波等を分解等することで、各種の解析を行い、また社会に有効な活用を行うことができることになる。この仕組みの概要については、次回以降の研究員の眼で紹介することしたい。
三角関数をグラフで表すと波形となり、いくつかの三角関数を組み合わせることで、複雑な波を形作ることができることがわかったと思う。
それでは、今回簡単に紹介したような電磁波や音波や地震波といった波は、実際にはどのような波形をしていて、それらを本当に三角関数で表現することができるのだろうか。
これについては、例えば、一定の周期を有する「周期関数」については、基本的には(「区分的に滑らかな」という条件を満たす場合には)、どんなに複雑でも、単純な波動の数学的な表現である正弦関数や余弦関数で表現することができる、ことが知られている。さらには、周期関数ではない関数も、(「区分的に滑らかで、かつ連続で、かつ絶対可積分」という条件を満たす場合には)、同様に三角関数で表現することができる。ここで用いられるのが、複雑な波を単純な波へと分解することになる数学的手法である「フーリエ級数展開」であり、「フーリエ変換」と呼ばれるものである。
こうした数学的手法があるからこそ、複雑な電波や光波や音波等を分解等することで、各種の解析を行い、また社会に有効な活用を行うことができることになる。この仕組みの概要については、次回以降の研究員の眼で紹介することしたい。
(2021年05月18日「研究員の眼」)
関連レポート
- 「三角関数」って、何でしたっけ?-sin(サイン)、cos(コサイン)、tan(タンジェント)-
- 数学記号の由来について(7)-三角関数(sin、cos、tan等)-
- 「三角関数」の基本的な定理とその有用性を再確認してみませんか(その2)-加法定理、二倍角、三倍角、半角の公式等-
- 「三角関数」の基本的な定理とその有用性を再確認してみませんか(その1)-正弦定理、余弦定理、正接定理-
- フィボナッチ数列について(その1)-フィボナッチ数列とはどのようなものでどんな性質を有しているのか-
- 「三角関数」と「波」の関係(その2)-電波によるデータ送信の仕組みと三角関数による「波」の表現の利用-
- 「三角関数」と「フーリエ変換」-三角関数の幅広い実社会利用での基礎となる重要な数学的手法-
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
| 2025/09/25 | 数字の「49」に関わる各種の話題-49という数字に皆さんはどんなイメージを有しているのだろう- | 中村 亮一 | 研究員の眼 |
新着記事
-
2025年10月16日
EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- -
2025年10月16日
再び不安定化し始めた米中摩擦-経緯の振り返りと今後想定されるシナリオ -
2025年10月15日
インド消費者物価(25年10月)~9月のCPI上昇率は1.5%に低下、8年ぶりの低水準に -
2025年10月15日
「生活の質」と住宅価格の関係~教育サービス・治安・医療サービスが新築マンション価格に及ぼす影響~ -
2025年10月15日
IMF世界経済見通し-世界成長率見通しは3.2%まで上方修正
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【「三角関数」と「波」の関係-三角関数による「波」の表現と各種の波(電磁波、音波、地震波等)-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
「三角関数」と「波」の関係-三角関数による「波」の表現と各種の波(電磁波、音波、地震波等)-のレポート Topへ



















 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




