- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 「三角関数」の基本的な定理とその有用性を再確認してみませんか(その1)-正弦定理、余弦定理、正接定理-
コラム
2021年04月02日
文字サイズ
- 小
- 中
- 大
正接定理
「余弦定理」と「正弦定理」と来れば、当然にtan(tangent)を意味する「正接」に由来する「正接定理」があるのではないかということになる。
「正接定理」は、三角形の2つの角と2つの辺の関係を示した定理で、以下の算式が成り立つというものである。
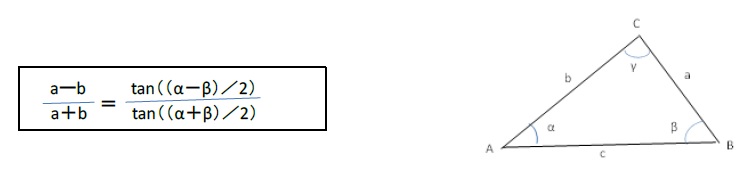
「正接定理」は、三角形の2つの角と2つの辺の関係を示した定理で、以下の算式が成り立つというものである。

これにより、三角形の2つの角と2辺の長さのうちどれか1つが不明の場合に、正弦定理の代わりにこの定理を使用しても残りの値を求めることができる。
実は、「余弦定理」と「正弦定理」についてはお聞き及びの方も多いと思われ、そういえばそんな定理を学んだよな、と思われるかもしれないが、「正接定理」については、そんなものあったかな、と思われる人が多いのではないかと思われる。実は、この「正接定理」は、「余弦定理」や「正弦定理」と比べて、一般的にはあまり利用されていない。このため、高校の数学等でも習わないようであり、馴染みが薄いものとなっている。
実は、「余弦定理」と「正弦定理」についてはお聞き及びの方も多いと思われ、そういえばそんな定理を学んだよな、と思われるかもしれないが、「正接定理」については、そんなものあったかな、と思われる人が多いのではないかと思われる。実は、この「正接定理」は、「余弦定理」や「正弦定理」と比べて、一般的にはあまり利用されていない。このため、高校の数学等でも習わないようであり、馴染みが薄いものとなっている。
この「正接定理」は、以下のように証明される。
「正弦定理」より、

とすると、
a=d sinα b=d sinβ
となることから、
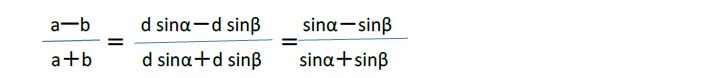
ここで、次回に述べる加法定理を用いると、
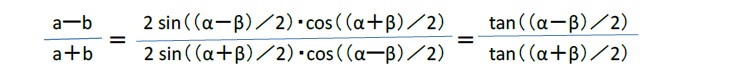
となる。
この「正接定理」により、三角形の2辺の長さとその間の角度γが与えられている場合に、
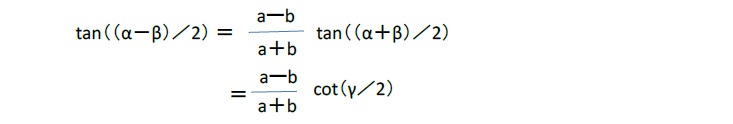
から、α-βを求めることができ、α+β(=180°―γ)も分かるので、αとβを求めることができることになる。
「正弦定理」より、

とすると、
a=d sinα b=d sinβ
となることから、
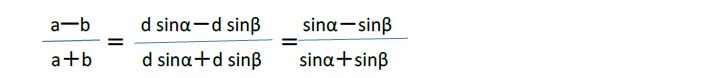
ここで、次回に述べる加法定理を用いると、
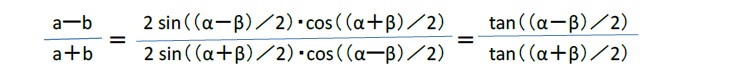
となる。
この「正接定理」により、三角形の2辺の長さとその間の角度γが与えられている場合に、
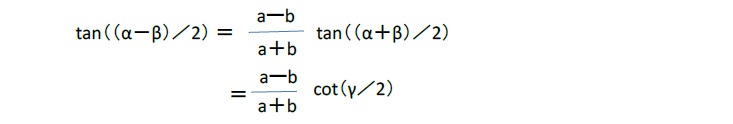
から、α-βを求めることができ、α+β(=180°―γ)も分かるので、αとβを求めることができることになる。
三角法
今回説明した三角関数の正弦定理や余弦定理は、いわゆる「三角法」と呼ばれる学問領域において、重要な役割を果たしている。「三角法」では、三角形の辺の長さや角の大きさの間の関係に基づいて、幾何学的図形の各要素の間の関係やそれらの利用・応用を研究している。
この「三角法」が利用されている分野として、例えば先に述べた「三角測量」が挙げられ、地図の作成や土地の位置・状態調査などを行う「測量」や天文学における「天文計算」に使用される。さらに、歴史的には、大洋における自らの船の位置を確認するための「航海術」としても利用されてきた。
光学的測距技術やGPS(全地球測位システム)等の各種技術の向上によって、こうした三角法の直接的利用は後退しているが、今日でも、三角法の考え方自体は、引き続き、測量、天文学、航海、計量学、兵器の照準等といった多くの目的に使用されている。
この「三角法」が利用されている分野として、例えば先に述べた「三角測量」が挙げられ、地図の作成や土地の位置・状態調査などを行う「測量」や天文学における「天文計算」に使用される。さらに、歴史的には、大洋における自らの船の位置を確認するための「航海術」としても利用されてきた。
光学的測距技術やGPS(全地球測位システム)等の各種技術の向上によって、こうした三角法の直接的利用は後退しているが、今日でも、三角法の考え方自体は、引き続き、測量、天文学、航海、計量学、兵器の照準等といった多くの目的に使用されている。
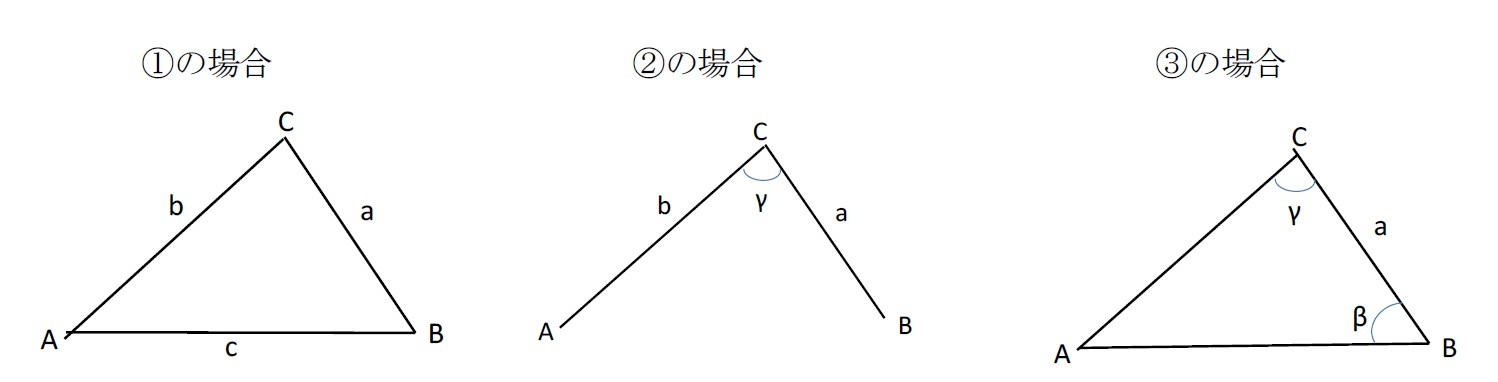
(参考)三角形の合同条件
三角形の辺や角に関する情報が与えられた時に、上記の定理を用いて、他の辺や角に関する情報を得ることができる。2つの三角形が「合同」であるとは、平行移動や回転や鏡映によって、一方の三角形が他方の三角形に重ね合わせることができる場合をいう。三角形の合同条件としては、以下の3つのケースが考えられる
①「三辺相等」:対応する3辺が等しい。
②「二辺挟角相等」: 2辺とその挟む角が等しい。
③「二角挟辺相等」:1辺とその両端の角が等しい。
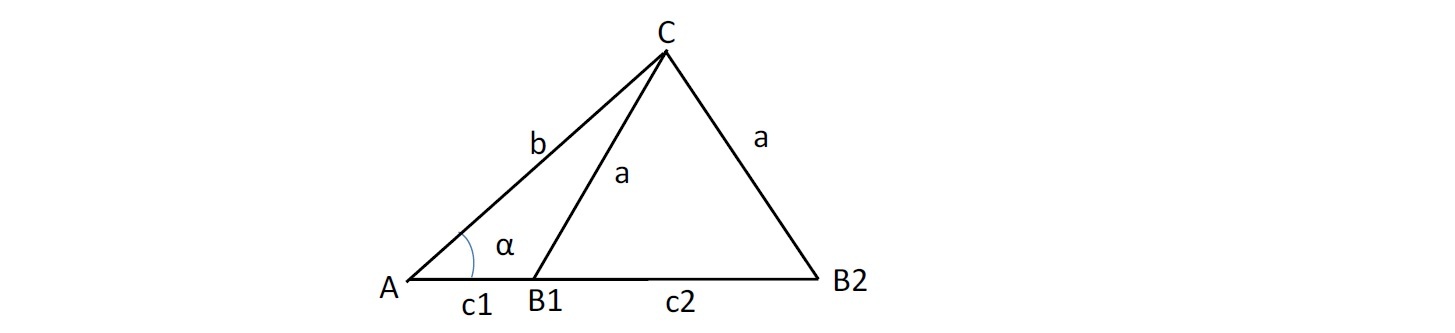
これらに加えて、④「一辺二角相等」ということで、2つの角とその間にない1辺が等しい場合も挙げられるが、三角形の内角の和が180°であることを考えれば、これは③に帰着するということもできる。
これを今回の定理との関係でみてみると、以下の通りとなる。
①の場合、「余弦定理」から3つの角度が求められる。
②の場合、「余弦定理」から、他の1辺が、さらに「余弦定理」から他の2つの角が求められる。
③の場合、三角形の内角の和が180°であることから、他の角が求まり、「正弦定理」から、他の2辺も求められる。
①「三辺相等」:対応する3辺が等しい。
②「二辺挟角相等」: 2辺とその挟む角が等しい。
③「二角挟辺相等」:1辺とその両端の角が等しい。
これらに加えて、④「一辺二角相等」ということで、2つの角とその間にない1辺が等しい場合も挙げられるが、三角形の内角の和が180°であることを考えれば、これは③に帰着するということもできる。
これを今回の定理との関係でみてみると、以下の通りとなる。
①の場合、「余弦定理」から3つの角度が求められる。
②の場合、「余弦定理」から、他の1辺が、さらに「余弦定理」から他の2つの角が求められる。
③の場合、三角形の内角の和が180°であることから、他の角が求まり、「正弦定理」から、他の2辺も求められる。
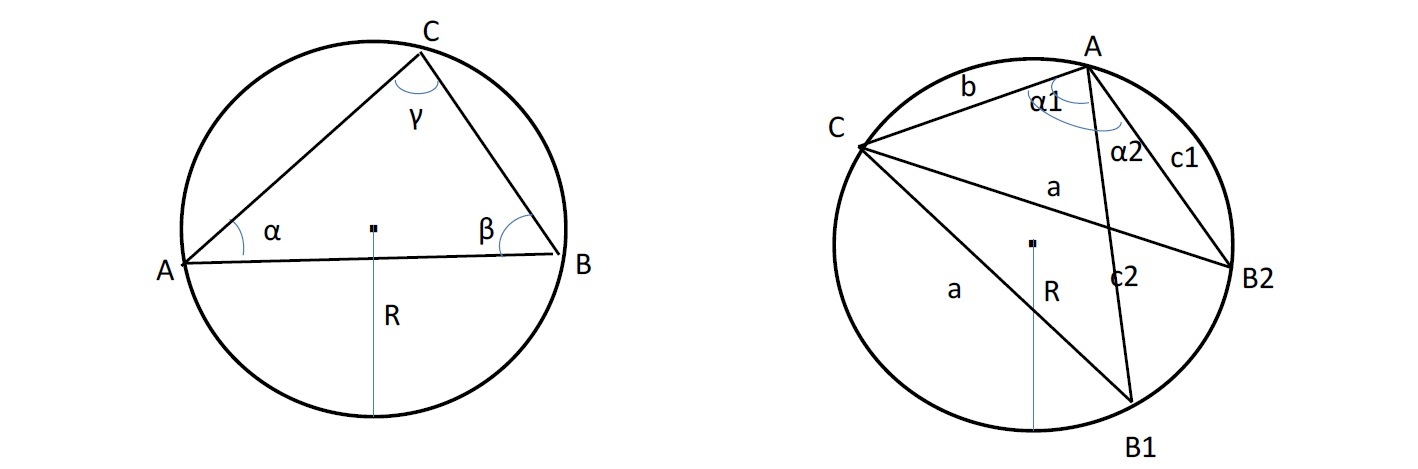
ただし、「⑥二辺と外接円半径」が与えられる場合には、上記の④のケースと同様に上の右図のように2通りの可能性が出てくる。
まとめ
以上、今回は「三角関数の性質」として、高校時代に学んだいくつかの公式や定理等のうち、「余弦定理」、「正弦定理」及び「正接定理」等の基本的な定理について、その有用性を含めて、紹介した。
次回の研究員の眼では、「三角関数の性質」として、高校時代に学んだいくつかの公式や定理等のうち、「加法定理」、「二倍角、三倍角、半角の公式」、「合成公式」、「和と積の変換公式」等について、その有用性とともに紹介したいと思う。
次回の研究員の眼では、「三角関数の性質」として、高校時代に学んだいくつかの公式や定理等のうち、「加法定理」、「二倍角、三倍角、半角の公式」、「合成公式」、「和と積の変換公式」等について、その有用性とともに紹介したいと思う。
(2021年04月02日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/11/13 | 数字の「27」に関わる各種の話題-27は3の3乗だが- | 中村 亮一 | 研究員の眼 |
| 2025/11/04 | 数字の「26」に関わる各種の話題-26という数字で思い浮かべる例は少ないと思われるが- | 中村 亮一 | 研究員の眼 |
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
新着記事
-
2025年11月14日
マレーシアGDP(2025年7-9月期)~内需は底堅く、外需は純輸出が改善 -
2025年11月14日
保険と年金基金における各種リスクと今後の状況(欧州 2025.10)-EIOPAが公表している報告書(2025年10月)の紹介 -
2025年11月14日
中国の不動産関連統計(25年10月)~販売が一段と悪化 -
2025年11月14日
英国GDP(2025年7-9月期)-前期比0.1%で2四半期連続の成長減速 -
2025年11月14日
家計消費の動向(二人以上世帯:~2025年9月)-「メリハリ消費」継続の中、前向きな変化の兆しも
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【「三角関数」の基本的な定理とその有用性を再確認してみませんか(その1)-正弦定理、余弦定理、正接定理-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
「三角関数」の基本的な定理とその有用性を再確認してみませんか(その1)-正弦定理、余弦定理、正接定理-のレポート Topへ




















 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




