- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- ディリクレの箱入れ原理
コラム
2024年07月03日
文字サイズ
- 小
- 中
- 大
大学受験数学で知る人ぞ知る「ディリクレの箱入れ原理」というものをご存知だろうか。別名「鳩の巣原理」とか「引き出し論法」とか、呼び方もさまざま。習ってないけど誰もが使える、そんな不思議な「ディリクレの箱入れ原理」について取り上げたい。
私の「研究員の眼」第一弾として、私の好きな大学受験数学からテーマを選んでみた。なぜ学校では習わないのか、習わないのになぜ使用可能なのか、論理的思考力のひとつであろう「現象を数理的裏付けによって説明する能力」を具体化したかのようなこの原理を皆様にも味わっていただければ幸いである。
私の「研究員の眼」第一弾として、私の好きな大学受験数学からテーマを選んでみた。なぜ学校では習わないのか、習わないのになぜ使用可能なのか、論理的思考力のひとつであろう「現象を数理的裏付けによって説明する能力」を具体化したかのようなこの原理を皆様にも味わっていただければ幸いである。
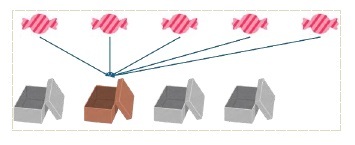 もちろん、同じ箱に飴が全部入る場合もある。「飴が5個入っている箱」がひとつと「空の箱」が3つという形だ。この場合も「飴が5個入っている箱」が「2つ以上飴が入っている箱」となる。
もちろん、同じ箱に飴が全部入る場合もある。「飴が5個入っている箱」がひとつと「空の箱」が3つという形だ。この場合も「飴が5個入っている箱」が「2つ以上飴が入っている箱」となる。状況が理解できただろうか。おそらく「当然じゃないか」と思ったのではないだろうか。そう、当然だからこそ「あえて習わないけど使って良い」という特殊なポジションにある原理なのだと筆者は理解している。
なお、5つの飴・4つの箱としたが、もちろんこの原理はもっと拡張され、
『1以上の自然数nに対して、n+1個の要素を、n個のグループに分けた時、少なくとも2つ以上の要素を持つグループがひとつ以上存在する』
が成り立つ。
では、これを用いると何か良いことがあるのだろうか。次節から具体例を見ていこう。
具体例 (1)
一辺が10メートルの正方形の的がある。ここに弾丸を101発打ち込んだ時、最も近い弾痕の距離は1.5メートル以内であることを示せ。ただし101発とも的に命中したものとする。
ディリクレの箱入れ原理の使い所はわかるだろうか。
一辺が10メートルの正方形の的がある。ここに弾丸を101発打ち込んだ時、最も近い弾痕の距離は1.5メートル以内であることを示せ。ただし101発とも的に命中したものとする。
ディリクレの箱入れ原理の使い所はわかるだろうか。
以上の10個の数字が該当する。
これらの数字のうち4の倍数であるような数が存在しているのは明らかだが、nが特定の数字でないときにも成り立つことを示さないといけない。仮にnが7や13のような素数であっても、はたまたどんな大きなnであっても必ずこの性質を満たす、というのが問題の趣旨である。
ここまで自由度が増すと、どこから取り掛かれば良いか悩ましくもなる。そこで役に立つのがディリクレの箱入れ原理である。解答例を書くには余白が足りないため省略するが、受験数学が好きな人はぜひ解いてみてほしい。(解答例は次ページへ)
今回は「学校では習わないのに受験に出てくるディリクレの箱入れ原理」をテーマに、研究員の眼として数学を学んできた者の視点を紹介した。ご好評いただければまた同様のテイストでご紹介したいと思う。
これらの数字のうち4の倍数であるような数が存在しているのは明らかだが、nが特定の数字でないときにも成り立つことを示さないといけない。仮にnが7や13のような素数であっても、はたまたどんな大きなnであっても必ずこの性質を満たす、というのが問題の趣旨である。
ここまで自由度が増すと、どこから取り掛かれば良いか悩ましくもなる。そこで役に立つのがディリクレの箱入れ原理である。解答例を書くには余白が足りないため省略するが、受験数学が好きな人はぜひ解いてみてほしい。(解答例は次ページへ)
今回は「学校では習わないのに受験に出てくるディリクレの箱入れ原理」をテーマに、研究員の眼として数学を学んできた者の視点を紹介した。ご好評いただければまた同様のテイストでご紹介したいと思う。
(2024年07月03日「研究員の眼」)

03-3512-1777
経歴
- 【職歴】
2007年 日本生命保険相互会社入社
2024年 ニッセイ基礎研究所
【加入団体等】
・日本アクチュアリー会 正会員
・年金数理人
植竹 康夫のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/07/23 | IAISグローバルセミナー開催~資産集約型再保険およびオルタナティブ資産に関するディスカッション~ | 植竹 康夫 | 保険・年金フォーカス |
| 2025/07/01 | 国際的に注目を集めるAsset-Intensive Reinsurance(AIR)を巡る動向 | 植竹 康夫 | 保険・年金フォーカス |
| 2025/06/12 | 寿命の限界と生命保険~限界寿命の延伸というパラダイムシフト~ | 植竹 康夫 | 研究員の眼 |
| 2025/04/01 | APRAによるガバナンス強化の提言について-オーストラリアの健全性規制 | 植竹 康夫 | 保険・年金フォーカス |
新着記事
-
2025年10月23日
御社のブランドは澄んでますか?-ブランド透明性が生みだす信頼とサステナビリティ開示のあり方(1) -
2025年10月23日
EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 -
2025年10月23日
中国:25年7~9月期GDPの評価-秋風索莫の気配が漂う中国経済。内需の悪化により成長率は減速 -
2025年10月23日
パワーカップルと小学校受験-データで読み解く暮らしの風景 -
2025年10月22日
高市新政権が発足、円相場の行方を考える~マーケット・カルテ11月号
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【ディリクレの箱入れ原理】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
ディリクレの箱入れ原理のレポート Topへ
























 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




