- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 計算の順番-ここではさらりと読み流してほしい
コラム
2021年03月30日
文字サイズ
- 小
- 中
- 大
今年の大学の数学の入試問題をみていたら、なぜか数年前に話題になっていたある話題を思い出した。小学生レベルの簡単な問題である。(掛け算記号の省略があるから中学生レベルか。)
問題 6÷2(1+2)=?
これだけである。頓智の問題ではない。まともな計算問題である。
小中学校以来の計算ルールは
・原則として左から計算する。
・カッコ内は先に計算する。
・掛け算・割り算は足し算・引き算より先に計算する。
・掛け算の記号は省略できる。
ということだろうか。それによれば、
(?) 6÷2(1+2)= 6÷2×(1+2)= 6÷2×3= 9 (答) (「9派」と呼んでおく)
とするのだろう。しかし特に計算を日常的にしている人であればあるほど何か違和感があって、そうはしないのではないか。私も引っ掛かる派である。
(?) 6÷2(1+2)= 6÷2(3)= 6÷6= 1 (答) (「1派」と呼んでおく)
のほうが実感にあうと思うのだが。
類似の式として 「2x÷2x」と書かれているのを見たら、これは1とみるのが自然なのではなかろうか?(この際「x=0の場合は・・」などというツッコミはなしで。)
2x÷2x = 2×x÷2×x = x2 とみること(人)があるだろうか。(これは後述)
違和感の原因は
・割り算の記号を使用している。(もう少し進んだ数学では分数表示をするから、あまり見かけない?)
・数値どうしの掛け算であって、文字式ではないのに掛け算記号を省略している。また掛け算を省略する際もせめて「・」くらい書くものだろう。(書いてもまったく解決しないが)
問題 6÷2(1+2)=?
これだけである。頓智の問題ではない。まともな計算問題である。
小中学校以来の計算ルールは
・原則として左から計算する。
・カッコ内は先に計算する。
・掛け算・割り算は足し算・引き算より先に計算する。
・掛け算の記号は省略できる。
ということだろうか。それによれば、
(?) 6÷2(1+2)= 6÷2×(1+2)= 6÷2×3= 9 (答) (「9派」と呼んでおく)
とするのだろう。しかし特に計算を日常的にしている人であればあるほど何か違和感があって、そうはしないのではないか。私も引っ掛かる派である。
(?) 6÷2(1+2)= 6÷2(3)= 6÷6= 1 (答) (「1派」と呼んでおく)
のほうが実感にあうと思うのだが。
類似の式として 「2x÷2x」と書かれているのを見たら、これは1とみるのが自然なのではなかろうか?(この際「x=0の場合は・・」などというツッコミはなしで。)
2x÷2x = 2×x÷2×x = x2 とみること(人)があるだろうか。(これは後述)
違和感の原因は
・割り算の記号を使用している。(もう少し進んだ数学では分数表示をするから、あまり見かけない?)
・数値どうしの掛け算であって、文字式ではないのに掛け算記号を省略している。また掛け算を省略する際もせめて「・」くらい書くものだろう。(書いてもまったく解決しないが)
なのかも、はっきりしないということである。
ところで、式を入力して計算できる関数電卓ならどちらの答えを出してくれるのか。
エクセルだと掛け算記号がどうしても必要だから、まぎれさせてくれないので、面白く(?)ない。グーグルの電卓機能だと「9」となる。ちなみに「2π÷2π」と入力してみると、「9.86…」と返ってくるので、(上記の「2x÷2x」のxにπを代入したものとして答えπ2 とする人(電卓?)が実際いるわけだ。どうも筆者には納得できかねるのだが・・・。)。
「2π÷(2π)」なら、もちろん「1」と出る。なお「6÷(1+2)」は「2」となり、「6÷1(1+2)」と入力すると「18」となる(ますます違和感あり!)。
なんにせよ「掛け算省略とみなし、左から計算」で一貫はしている。(しかし「1派」の筆者は、この電卓を敬して遠ざけることにしたい!)
これがもし、マークシート式などの試験問題として出題されたら答えはどちらだろうか(実際に高校入試では、文字式の計算として類似の問題はよくでているように見える)。答えはひとつしか認められないだろうし、計算過程、補足、説明など一切書くことはできない。こういう単発のクイズ的な出題が全く意味のないものであって、考えている状況や背景があっての数式ではないかとも思う。実際の現場?では、問題の意味をその都度確認すればよいし、必要なら ( )をつけるなりして、意図する計算を明確にすれば解決すると思う。
なお、これに関して文部科学省の中学校学習指導要領をざっとみてみたが、明確な記載は見当たらないようだ(筆者の見落としかもしれないし、何らかの解釈があるのかもしれない。)。
この話は、数年前に台湾で議論になったのがきっかけだそうで、もとは「9が正解」という教訓を意図したらしいが、意外に「9派」と「1派」はほぼ半々だったようだ。あるいは曖昧なら( )を使うなどしてもっときちんと書けとも。日本でも一部で話題となり、いろいろな立場(数学そのものの記法、決めている主体、教育の仕方など)があり、これだけで「炎上」に近い議論になるらしい(だからここでしないで下さい。)。筆者はこれまで計算が必要な業務に従事し、数学の本を比較的多く見てもいるが、この種の計算で曖昧さを感じたことは、ない。皆様も余計な議論に時間を割く余裕もないだろうから、そんな話もあるのか程度に、ここではさらりと読み流してほしい。
ところで、式を入力して計算できる関数電卓ならどちらの答えを出してくれるのか。
エクセルだと掛け算記号がどうしても必要だから、まぎれさせてくれないので、面白く(?)ない。グーグルの電卓機能だと「9」となる。ちなみに「2π÷2π」と入力してみると、「9.86…」と返ってくるので、(上記の「2x÷2x」のxにπを代入したものとして答えπ2 とする人(電卓?)が実際いるわけだ。どうも筆者には納得できかねるのだが・・・。)。
「2π÷(2π)」なら、もちろん「1」と出る。なお「6÷(1+2)」は「2」となり、「6÷1(1+2)」と入力すると「18」となる(ますます違和感あり!)。
なんにせよ「掛け算省略とみなし、左から計算」で一貫はしている。(しかし「1派」の筆者は、この電卓を敬して遠ざけることにしたい!)
これがもし、マークシート式などの試験問題として出題されたら答えはどちらだろうか(実際に高校入試では、文字式の計算として類似の問題はよくでているように見える)。答えはひとつしか認められないだろうし、計算過程、補足、説明など一切書くことはできない。こういう単発のクイズ的な出題が全く意味のないものであって、考えている状況や背景があっての数式ではないかとも思う。実際の現場?では、問題の意味をその都度確認すればよいし、必要なら ( )をつけるなりして、意図する計算を明確にすれば解決すると思う。
なお、これに関して文部科学省の中学校学習指導要領をざっとみてみたが、明確な記載は見当たらないようだ(筆者の見落としかもしれないし、何らかの解釈があるのかもしれない。)。
この話は、数年前に台湾で議論になったのがきっかけだそうで、もとは「9が正解」という教訓を意図したらしいが、意外に「9派」と「1派」はほぼ半々だったようだ。あるいは曖昧なら( )を使うなどしてもっときちんと書けとも。日本でも一部で話題となり、いろいろな立場(数学そのものの記法、決めている主体、教育の仕方など)があり、これだけで「炎上」に近い議論になるらしい(だからここでしないで下さい。)。筆者はこれまで計算が必要な業務に従事し、数学の本を比較的多く見てもいるが、この種の計算で曖昧さを感じたことは、ない。皆様も余計な議論に時間を割く余裕もないだろうから、そんな話もあるのか程度に、ここではさらりと読み流してほしい。
(2021年03月30日「研究員の眼」)

03-3512-1833
経歴
- 【職歴】
1987年 日本生命保険相互会社入社
・主計部、財務企画部、調査部、ニッセイ同和損害保険(現 あいおいニッセイ同和損害保険)(2007年‐2010年)を経て
2012年 ニッセイ基礎研究所
【加入団体等】
・日本アクチュアリー会 正会員
・日本証券アナリスト協会 検定会員
安井 義浩のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/31 | 保険型投資商品の特徴を理解すること(欧州)-欧州保険協会の解説文書 | 安井 義浩 | 保険・年金フォーカス |
| 2025/10/24 | 企業年金の改定についての技術的なアドバイス(欧州)-EIOPAから欧州委員会への回答 | 安井 義浩 | 保険・年金フォーカス |
| 2025/10/17 | EUの金融システムのリスクと脆弱性(2025秋)-欧州の3つの金融監督当局の合同委員会報告書 | 安井 義浩 | 基礎研レター |
| 2025/10/10 | 保険・年金関係の税制改正要望(2026)の動き-関係する業界・省庁の改正要望事項など | 安井 義浩 | 基礎研レター |
新着記事
-
2025年11月04日
今週のレポート・コラムまとめ【10/28-10/31発行分】 -
2025年10月31日
交流を広げるだけでは届かない-関係人口・二地域居住に求められる「心の安全・安心」と今後の道筋 -
2025年10月31日
ECB政策理事会-3会合連続となる全会一致の据え置き決定 -
2025年10月31日
2025年7-9月期の実質GDP~前期比▲0.7%(年率▲2.7%)を予測~ -
2025年10月31日
保険型投資商品の特徴を理解すること(欧州)-欧州保険協会の解説文書
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【計算の順番-ここではさらりと読み流してほしい】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
計算の順番-ここではさらりと読み流してほしいのレポート Topへ

















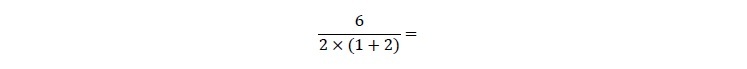
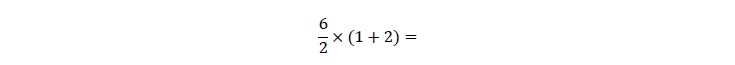

 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




