大きな（または小さな）数字の表し方ー単位の話に出てくる数の表記の仕方など

保険研究部主任研究員年金総合リサーチセンター・気候変動リサーチセンター兼任安井義浩

このレポートの関連カテゴリ

理科年表によると、電子の質量は
9.10938356　×10^-31　㎏
などという記載がある。

重さの単位を言う前に、ついでだから、こうしたところで使われる、数字の書き方などの話をしよう。

【理系？編】
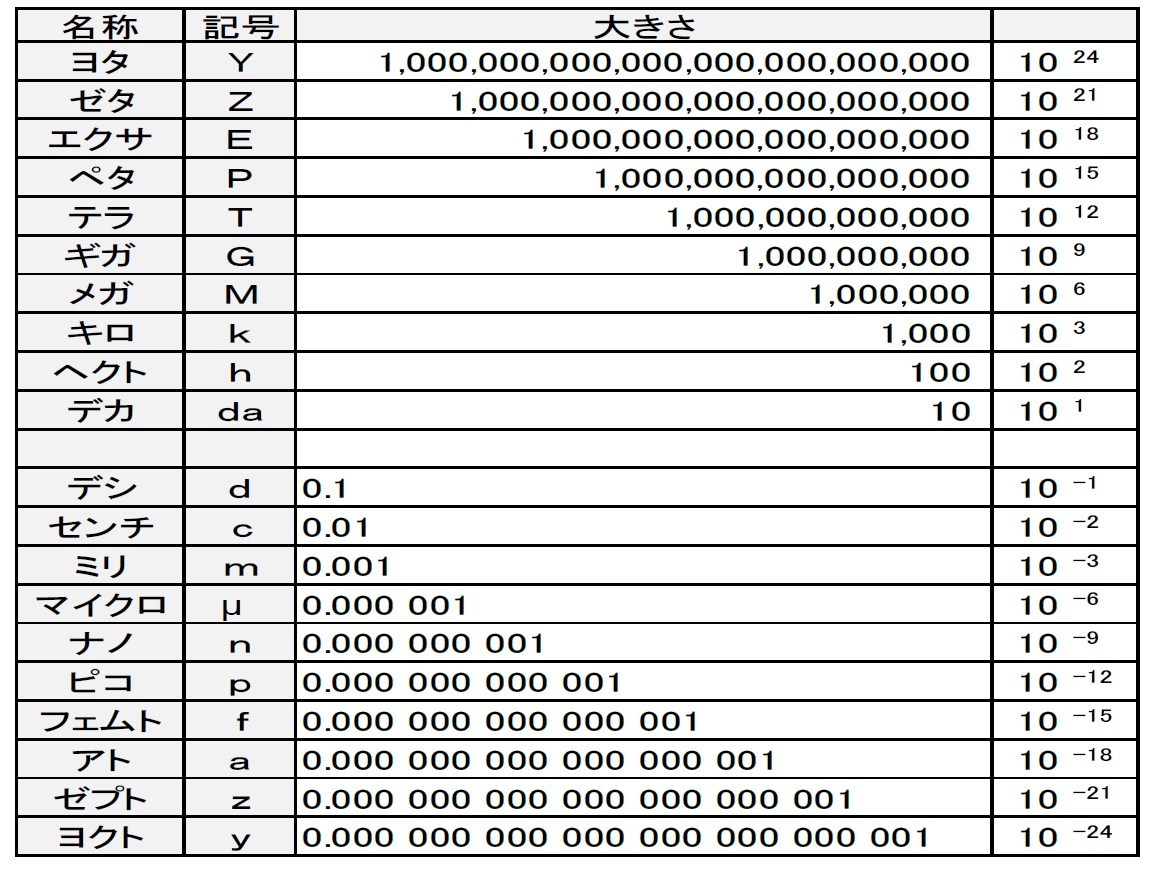
10の整数倍を表す接頭語^*1

これらは、理科年表にも記載されている通り、科学の世界では標準的なものである。あまり大きくも小さくもない接頭語は、日常耳にするものも多いだろう。

大きいほうでは、キロは馴染み深いし、ヘクトは「ヘクトパスカル」などという単位が台風情報でよく使われるのを耳にする。さらに大きいところでは、スマホなどのデータ量とかで、「メガバイト（MB）」、「ギガバイト(GB)」などまではよく見聞きするだろう。

（ところが、こうした情報分野では2進法がよく使われることもあって、データ量の単位「バイト」については、単純に1000倍ではなく1024＝2¹⁰倍毎に、呼び方が昇格するそうだが。）

小さいほうは、ミリ、マイクロなどは日常的にでてくるかもしれない。

さらに「ナノ」は、超小型の世界の技術を「ナノテクノロジー」と呼ぶことから耳にすることがあろう。この呼び名は、10^-9　ｍの世界、だいたい原子・分子のスケールで、素材などを制御する技術であることから来ている。

【文系？編】
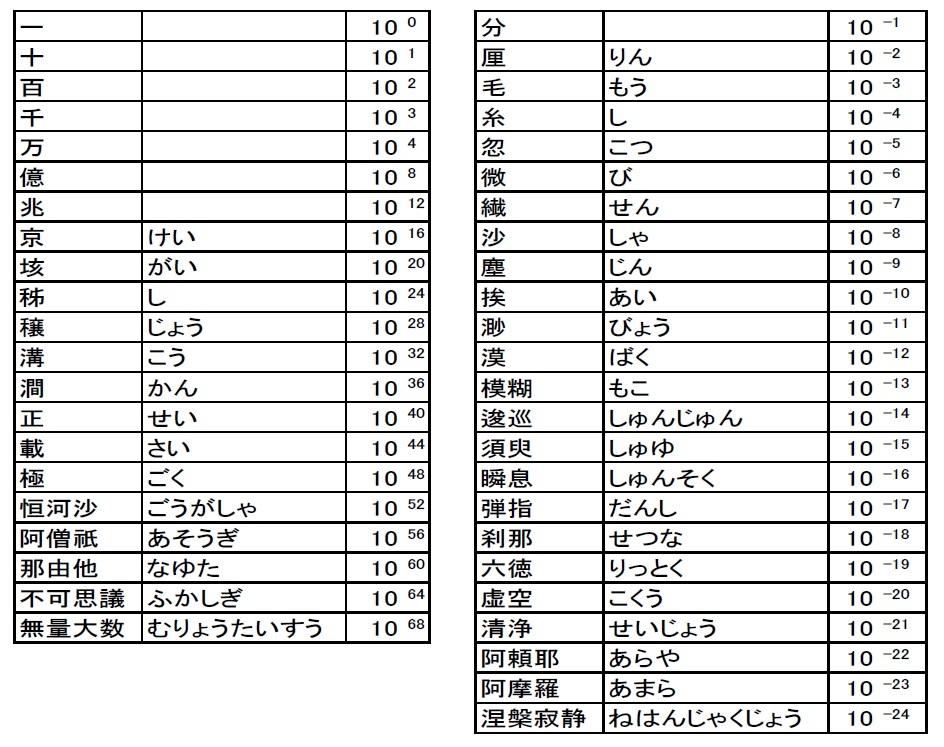
難しい漢字が多いので文系？編とでも呼んで、別の方面からの数の単位の呼称を見てみよう^*2。

日常使うのは、国の予算とかＧＤＰとかで見る「兆」までだろうか（だから読み方は省略）。「京」になると怪しいが、割と知られているのではなろうか。それ以上は使う場面がめったになさそうだ。科学分野ならば、表の右に記したように「10のなん乗」と数字で書くから、呼び方など知らなくてもなんとかなる。（むしろ国際的にも通用する。）

小さいほうは、野球の打率などで「毛」まで、あるいは「糸」までを使うか。ただ仕事によってはこういうのを日常的に使っている人もいるかもしれない。

野球の打率といえば、例えば「3割2分1厘」などという。だから「「分」は100分の1だ（？）」という誤解がある（というか、日頃は考えもしないが。）。しかし別の場面では、「七分咲き」、「腹八分目」、「五分五分」などのように10分の1の意味で使うことが多い。すると「割」はどこにいった？と思うかもしれない。「割」も10分の1の表現であるが、先ほどの打率などの表現では「分は割に対しての10分の1」を表しているそうな。

3割2分1厘　＝「3.21割」＝　３割＋　1割の1／10が2個　＋1割の1／100が1個と解釈すべきだそうだ。

単独で話題にするのも気が引けるので、ついでに、これらの表にでてくる「マイナス乗」とか、「ゼロ乗」について補足しておく。

ナントカの0乗は1である。

10のマイナス3乗は1／（10の3乗）である、など。

これらは、何乗という部分が「掛け算なのに、足し算になる」規則を通用させるために、以下のように、決めたのである。

素朴なほうからいくと、例えば
10³＝10×10×10
などである。肩に乗っている回数だけ、もとの数値をかけあわせればよい。

また
10²×10³　　＝　（10×10×10）×（10×10）＝　10²^＋3＝　10⁵　
となどと、全体は掛け算なのに、肩の数字は「足し算」すればよい。

これが一番大切なところである。このことが、マイナスの数字でも、ゼロでも成り立ってくれればいいのに。この願いをかなえるようにすると、例えば
10²⁺⁰＝10²×10⁰　　普通に書くと　100＝100×10⁰

だから、ここは　10⁰＝1　であってくれればいい。というわけで、ゼロ以外の数字のゼロ乗は1と取り決める。

さらに、肩にのっている数字が引き算でも、そうしてよいとすれば、例えば
1　＝　10⁰　＝　10^2-2　＝　10²×10^-2
だから、10^-2は10²の逆数であってくれれば、すべてうまくいく。

これで肩に乗る数は、自然数だけでなくどんな整数でも、足し引きする計算をしてもよいことになった。また今の話の中では「10の」なん乗としてきたが、10の代わりにどんな数でもいい。^*3
この先は、肩に乗る数について、整数ばかりでなく分数でもいいし、分数で表されない√２のような無理数でも成り立つように、という感じでうまく決めていく。最後は複素数（２乗して-1になる数ｉも含めた数）でも定義することができて、だいたい自然に計算できるようになっている。

究極的には、例えば、ｉ^ｉなどという数も計算できるが、やめておく。理工系学生向けでない出版物は、算式が一つあるごとに、販売部数が半減する、と何かで読んだ記憶がある（別にかまわないが。）。

^*1 理科年表2018版
^*2 これは、理系編と違って、理科年表にあるような正式の定義かどうかは確認できない。諸説ある部分も含まれている。
^*3 実は0だけはちょっと都合が悪いので、0⁰は考えない。またマイナスの数の何乗は相当ややこしくなるので、それを考えたいなら、本格的に勉強したほうが、こんないい加減な解説を読むよりいいだろう。

日付	タイトル	執筆者	媒体
2025/04/25	年金や貯蓄性保険の可能性を引き出す方策の推進（欧州）－貯蓄投資同盟の構想とEIOPA会長の講演録などから	安井義浩	基礎研レター
2025/04/18	金融セクターにおけるリスクと脆弱性（欧州　2025春）－ESAの合同報告書より。地政学的リスクとサイバーリスクに重点。	安井義浩	基礎研レター
2025/04/11	バミューダ金融当局の2025事業計画－今後再保険などで注目されるかもしれない。	安井義浩	基礎研レター
2025/03/21	宇宙天気現象に関するリスク－太陽フレアなどのピークに入っている今日この頃	安井義浩	基礎研レポート

日付

タイトル

執筆者

媒体

2025/04/25

年金や貯蓄性保険の可能性を引き出す方策の推進（欧州）－貯蓄投資同盟の構想とEIOPA会長の講演録などから

安井義浩

基礎研レター

2025/04/18

金融セクターにおけるリスクと脆弱性（欧州　2025春）－ESAの合同報告書より。地政学的リスクとサイバーリスクに重点。

安井義浩

基礎研レター