- シンクタンクならニッセイ基礎研究所 >
- 曲線にはどんな種類があって、どう社会に役立っているのか(その5)-サイクロイド(その性質等)-
コラム
2024年05月09日
文字サイズ
- 小
- 中
- 大
最速降下曲線と等時降下曲線
「サイクロイド」は別名として「最速降下曲線」とも呼ばれる。その意味するところは、物をサイクロイド曲線(の上下逆の形)に沿って転がした時に、物が一番早く転がり落ちる曲線、になっている(あくまでも、摩擦がなく、重力の作用だけに因るケースで、これは物の重さにはよらない)。
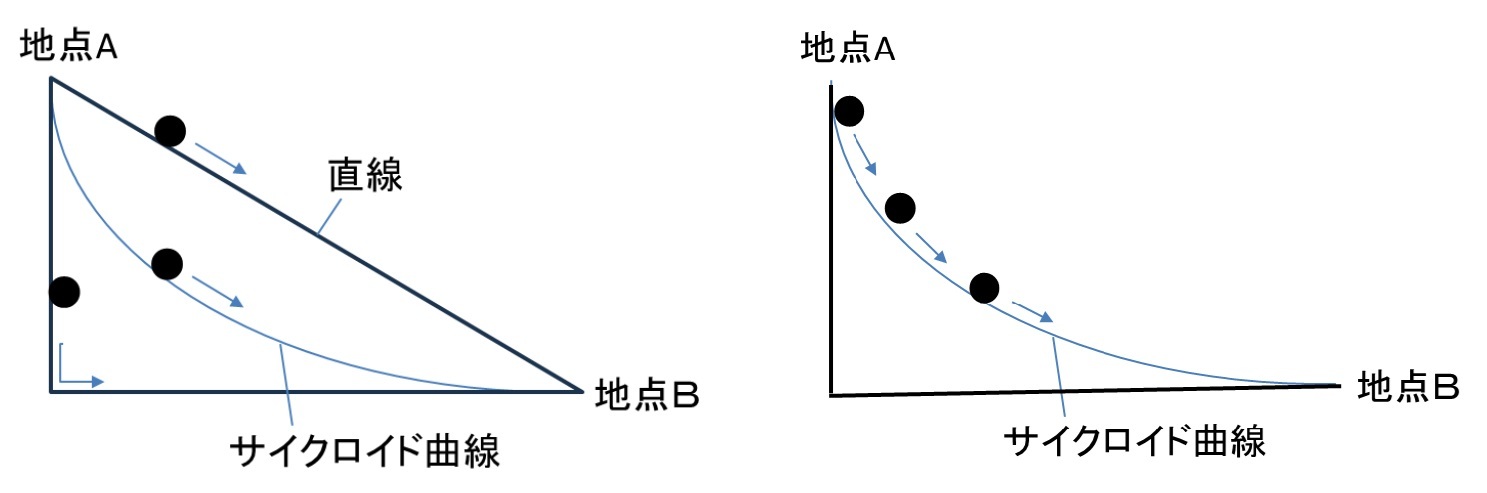
下図のように地点Aから地点Bに向けて物を落下させる時、いくつかのルート(直線を含む曲線)が考えられる。この時に、直線ルートが最も早いのではないかと考える人も多いのではないかと思われる。ところが、物体が落下する時の加速度は傾斜が大きいほど大きくなり、速度は次第に早くなっていくが、直線ルートの場合、当初の速度はあまり速くなく、最下点に到達する時が最も速度が速くなることになる。一方で、単純に地点Bの高さに落下するだけであれば、ほぼ直角に落下するのが最も速くなるが、その後の水平な直線を移動するのに距離が長くなっていることもあり、遅くなってしまう。その意味では、できる限り早く最速速度に到達しつつ、できる限り短い距離を行くルートが望まれることになる。こうした2つの要件のバランス感の中で、最も早く滑り落ちることができる曲線が決定されていくことになる。
この問題に対して、ガリレオ・ガリレイ5は、最速降下曲線は円弧であると考えていたようだ。ところが、実はサイクロイド曲線が最速降下曲線になっていることが証明されている。
さらに言えば、サイクロイド曲線は「等時降下曲線」とも呼ばれる。その意味するところは、サイクロイド曲線上のどの地点から物を転がしても、最下点に到達するまでの時間が等しくなる、ということになる。多くの皆さんは本当だろうかと思われるだろう。因みに、直線ルートの場合には、我々の直感に合致するように、最も地点Bに近い物が最も早く地点Bに到達する。ところが、サイクロイド曲線の場合には、地点Aに近い物は、当初の傾きが大きく、加速度も大きくなることから、結局は地点Bに近い物と同時に地点Bに到達することになる。
下図のように地点Aから地点Bに向けて物を落下させる時、いくつかのルート(直線を含む曲線)が考えられる。この時に、直線ルートが最も早いのではないかと考える人も多いのではないかと思われる。ところが、物体が落下する時の加速度は傾斜が大きいほど大きくなり、速度は次第に早くなっていくが、直線ルートの場合、当初の速度はあまり速くなく、最下点に到達する時が最も速度が速くなることになる。一方で、単純に地点Bの高さに落下するだけであれば、ほぼ直角に落下するのが最も速くなるが、その後の水平な直線を移動するのに距離が長くなっていることもあり、遅くなってしまう。その意味では、できる限り早く最速速度に到達しつつ、できる限り短い距離を行くルートが望まれることになる。こうした2つの要件のバランス感の中で、最も早く滑り落ちることができる曲線が決定されていくことになる。
この問題に対して、ガリレオ・ガリレイ5は、最速降下曲線は円弧であると考えていたようだ。ところが、実はサイクロイド曲線が最速降下曲線になっていることが証明されている。
さらに言えば、サイクロイド曲線は「等時降下曲線」とも呼ばれる。その意味するところは、サイクロイド曲線上のどの地点から物を転がしても、最下点に到達するまでの時間が等しくなる、ということになる。多くの皆さんは本当だろうかと思われるだろう。因みに、直線ルートの場合には、我々の直感に合致するように、最も地点Bに近い物が最も早く地点Bに到達する。ところが、サイクロイド曲線の場合には、地点Aに近い物は、当初の傾きが大きく、加速度も大きくなることから、結局は地点Bに近い物と同時に地点Bに到達することになる。
「等時降下曲線」がサイクロイド曲線であることは、1659年にオランダの数学者・物理学者・天文学者であるクリスティアーン・ホイヘンス(Christiaan Huygens)によって証明された。また、1696年にヨハン・ベルヌーイによって提示された「最速降下曲線問題(最速降下曲線が何であるか)」は、4人の数学者(アイザック・ニュートン、ヤコブ・ベルヌーイ(ヨハンの兄)、ゴットフリート・ライプニッツ、ギヨーム・ド・ロピタル)によって、サイクロイド曲線であるということで、解かれている。
この問題の解決の過程で、ヤコブ・ベルヌーイは新しい手法を開発し、それがレオンハルト・オイラーによって改良され、後に「変分法」と呼ばれるものになっている。さらに、ジョゼフ=ルイ・ラグランジュは現代の微積分学に帰着する仕事を進め、ニュートンとライプニッツの間の異なった競争もこの発展に貢献している、というように、この問題はかなり興味深いテーマとつながりを有している。
5 ガリレオ・ガリレイは、サイクロイドという用語を考案し、曲線を真剣に研究した最初の人物と言われている。
この問題の解決の過程で、ヤコブ・ベルヌーイは新しい手法を開発し、それがレオンハルト・オイラーによって改良され、後に「変分法」と呼ばれるものになっている。さらに、ジョゼフ=ルイ・ラグランジュは現代の微積分学に帰着する仕事を進め、ニュートンとライプニッツの間の異なった競争もこの発展に貢献している、というように、この問題はかなり興味深いテーマとつながりを有している。
5 ガリレオ・ガリレイは、サイクロイドという用語を考案し、曲線を真剣に研究した最初の人物と言われている。
ここで、aとbとθについては、定円の半径a、動円の半径b、回転角θを表している。
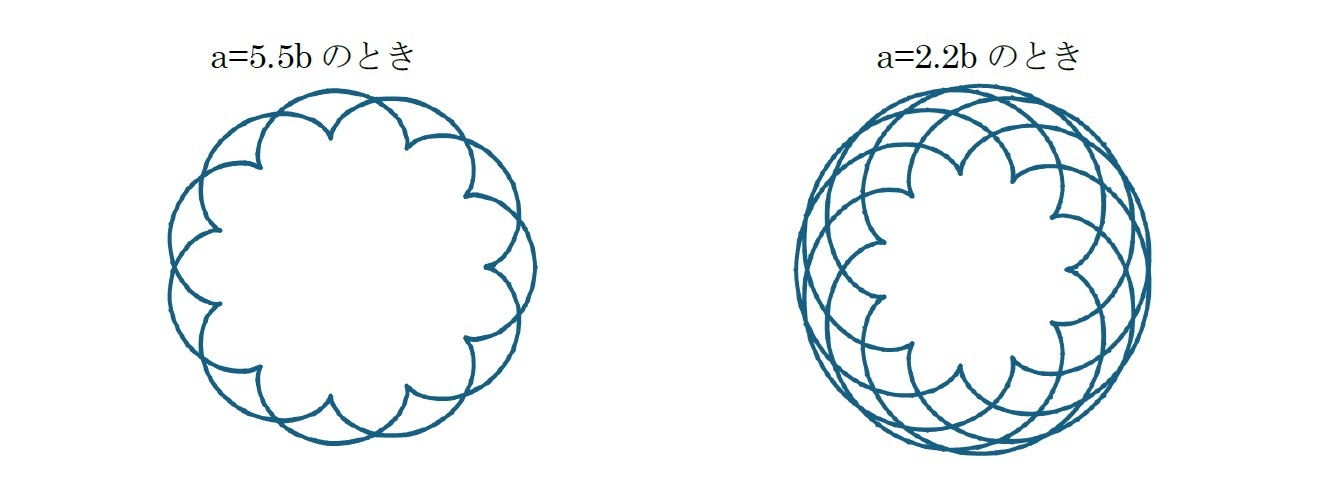
aとbの関係が特定の状況下では、先に示した図にように、a=bのときが「カージオイド(cardioid)(心臓形)」、a=2bのときが「ネフロイド(nephroid)(腎臓形)」、a=3bのときが「トレフォイロイド(Trefoiloid)」、a=4b のときが「クアトロフォイロイド(Quatrefoiloid)」と呼ばれる図形になる。
このように、a=nb のとき、n個の「尖点(cusp)」6を有している。
また、a=nb のときの弧長(円が1回転した時の定点の軌跡の長さ)ℓと面積(弧で囲まれた部分)Sについては、以下の通りとなる(先に述べたサイクロイドと同様の考え方で算出できる)。
aとbの関係が特定の状況下では、先に示した図にように、a=bのときが「カージオイド(cardioid)(心臓形)」、a=2bのときが「ネフロイド(nephroid)(腎臓形)」、a=3bのときが「トレフォイロイド(Trefoiloid)」、a=4b のときが「クアトロフォイロイド(Quatrefoiloid)」と呼ばれる図形になる。
このように、a=nb のとき、n個の「尖点(cusp)」6を有している。
また、a=nb のときの弧長(円が1回転した時の定点の軌跡の長さ)ℓと面積(弧で囲まれた部分)Sについては、以下の通りとなる(先に述べたサイクロイドと同様の考え方で算出できる)。
6 移動する点が方向を逆にしなければならない曲線状の点で、曲線の特異点と呼ばれるものの一種。
ここで、aとbとθについては、定円の半径a、動円の半径b、回転角θを表している。
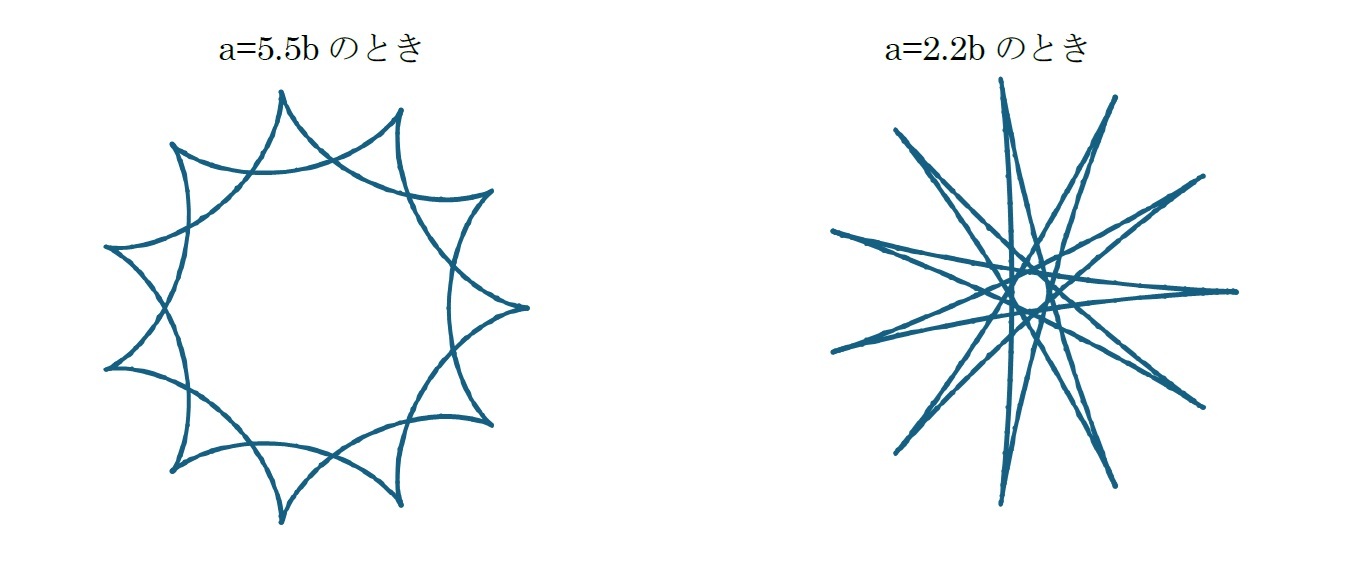
aとbの関係が特定の状況下では、a=3bのときが「デルトイド(deltoid)(三芒形)」又は「スタイナー曲線(Steiner curve)」、a=4bのときが「アステロイド(astroid)(星芒形)」7、a=5bのときが「ペントイド(pentoid)(五芒形)」、a=6bのときが「エグゾイド(exoid)(六芒形)」と呼ばれる図形になる。
このように、a=nb のとき、n個の「尖点(cusp)」を有している(a=2bのときは、直線になり、これは2つの尖点を有している8)。
また、a=nb のときの弧長(円が1回転した時の定点の軌跡の長さ)ℓと面積(弧で囲まれた部分)Sについては、以下の通りとなる(先に述べたサイクロイドと同様の考え方で算出できる)。
aとbの関係が特定の状況下では、a=3bのときが「デルトイド(deltoid)(三芒形)」又は「スタイナー曲線(Steiner curve)」、a=4bのときが「アステロイド(astroid)(星芒形)」7、a=5bのときが「ペントイド(pentoid)(五芒形)」、a=6bのときが「エグゾイド(exoid)(六芒形)」と呼ばれる図形になる。
このように、a=nb のとき、n個の「尖点(cusp)」を有している(a=2bのときは、直線になり、これは2つの尖点を有している8)。
また、a=nb のときの弧長(円が1回転した時の定点の軌跡の長さ)ℓと面積(弧で囲まれた部分)Sについては、以下の通りとなる(先に述べたサイクロイドと同様の考え方で算出できる)。
7 英語は「astroid」であり、「asteroid」(小惑星)ではないので、日本語では「アストロイド」と呼ぶべきと思われるが、通常「アステロイド」と呼んでいる。また、アステロイドの媒介変数表示は、3倍角の公式を用いて、以下の通りとなる。
8 小さな円がその直径の2倍の直径を持つ大きな円の内側に沿って回転する数学的メカニズムを「トゥースィーの対円(Tusi couple又はTusi's mechanism)」と呼んでいる。小さな円の回転により、この円の円周上の点が、大きな円の直径に沿って往復する形になっている。
最後に
以上、今回は、「サイクロイド曲線」について、その内容や基本的な性質等について報告してきた。
直線上の円運動に伴う特定の点の運動という、ある意味で単純な運動の軌跡が、実は極めて重要な意味合いを持つ曲線を描く、ということは何とも興味深い話ではないだろうか。自然に見られる各種の運動の動きは、実は単純な動きで示されるものに支配(?)されているということになる。
また、媒介変数表示によって、各種の曲線を表すことができることがわかっていただけたと思う。さらには、これらの媒介変数の算式等を若干変更することで、思わぬ曲線が現れてくることにもなる。
次回の研究員の眼では、「トロコイド」、「パスカルの蝸牛形」とも呼ばれる「リマソン」及び今回の研究員の眼でも簡単に紹介している「カージオイド」等について報告する。
直線上の円運動に伴う特定の点の運動という、ある意味で単純な運動の軌跡が、実は極めて重要な意味合いを持つ曲線を描く、ということは何とも興味深い話ではないだろうか。自然に見られる各種の運動の動きは、実は単純な動きで示されるものに支配(?)されているということになる。
また、媒介変数表示によって、各種の曲線を表すことができることがわかっていただけたと思う。さらには、これらの媒介変数の算式等を若干変更することで、思わぬ曲線が現れてくることにもなる。
次回の研究員の眼では、「トロコイド」、「パスカルの蝸牛形」とも呼ばれる「リマソン」及び今回の研究員の眼でも簡単に紹介している「カージオイド」等について報告する。
(2024年05月09日「研究員の眼」)
このレポートの関連カテゴリ
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
新着記事
-
2025年11月04日
今週のレポート・コラムまとめ【10/28-10/31発行分】 -
2025年10月31日
交流を広げるだけでは届かない-関係人口・二地域居住に求められる「心の安全・安心」と今後の道筋 -
2025年10月31日
ECB政策理事会-3会合連続となる全会一致の据え置き決定 -
2025年10月31日
2025年7-9月期の実質GDP~前期比▲0.7%(年率▲2.7%)を予測~ -
2025年10月31日
保険型投資商品の特徴を理解すること(欧州)-欧州保険協会の解説文書
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【曲線にはどんな種類があって、どう社会に役立っているのか(その5)-サイクロイド(その性質等)-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
曲線にはどんな種類があって、どう社会に役立っているのか(その5)-サイクロイド(その性質等)-のレポート Topへ


















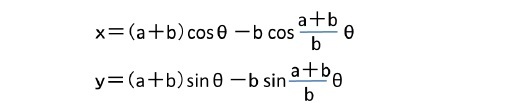
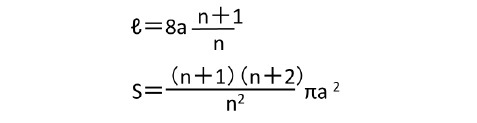
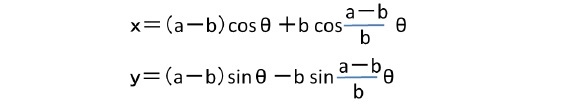
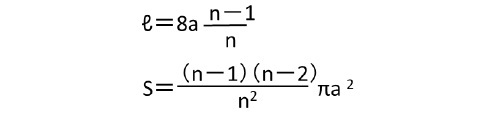

 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




