- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 無限について(その6)-無限級数について-
コラム
2022年11月21日
文字サイズ
- 小
- 中
- 大
はじめに
無限に関する前々回までの4回の研究員の眼で、無限に関するパラドックスを紹介してきた。また、前回の研究員の眼では、無限大(∞)に関する話題について、無限数列の和、差、積、商について、紹介した。そこでは、あくまでも「無限数列」を対象にしており、無限数列を前から順番に加えていって得られる「無限級数」については述べていなかった。
今回は、無限級数に関する話題について紹介したい。
今回は、無限級数に関する話題について紹介したい。
を、数列{an}の「第N部分和」というが、この部分和からなる数列{SN}の収束、発散が、無限級数の収束、発散を意味することになる。
なお、有限数列についても、有限個の項以外は0として、無限数列とみなすことで、上記の定義に従うことができる。一般的に「級数」と呼ばれるが、無限個の和であることを強調する場合には「無限級数」と呼ばれることになる。以下では、「無限級数」の用語を使用することにする。
なお、有限数列についても、有限個の項以外は0として、無限数列とみなすことで、上記の定義に従うことができる。一般的に「級数」と呼ばれるが、無限個の和であることを強調する場合には「無限級数」と呼ばれることになる。以下では、「無限級数」の用語を使用することにする。
無限級数の例
γについては、超越数であると予想されているが、いまだ無理数であるかどうかも証明されていない。
この値は、ほぼ以下の通りとなる。
Ψ=3.35988566624317755・・・
なお、Ψは無理数であることが知られているが、超越数であるか否かはわかっていない。
Ψ=3.35988566624317755・・・
なお、Ψは無理数であることが知られているが、超越数であるか否かはわかっていない。
(2022年11月21日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
新着記事
-
2025年10月24日
米連邦政府閉鎖と代替指標の動向-代替指標は労働市場減速とインフレ継続を示唆、FRBは政府統計を欠く中で難しい判断を迫られる -
2025年10月24日
企業年金の改定についての技術的なアドバイス(欧州)-EIOPAから欧州委員会への回答 -
2025年10月24日
消費者物価(全国25年9月)-コアCPI上昇率は拡大したが、先行きは鈍化へ -
2025年10月24日
保険業界が注目する“やせ薬”?-GLP-1は死亡率改善効果をもたらすのか -
2025年10月23日
御社のブランドは澄んでますか?-ブランド透明性が生みだす信頼とサステナビリティ開示のあり方(1)
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【無限について(その6)-無限級数について-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
無限について(その6)-無限級数について-のレポート Topへ

















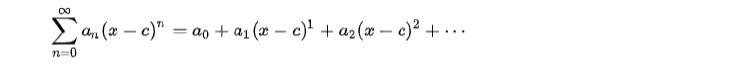
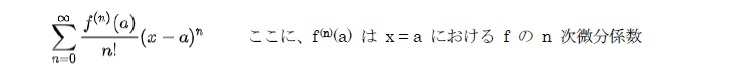


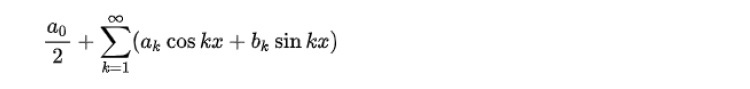


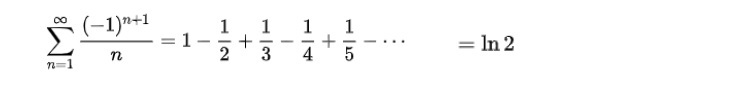
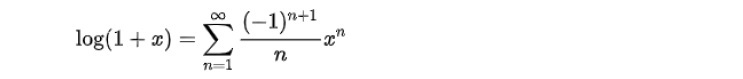
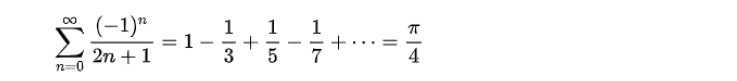
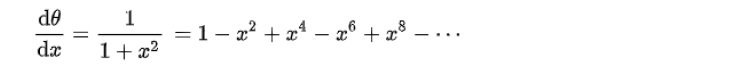


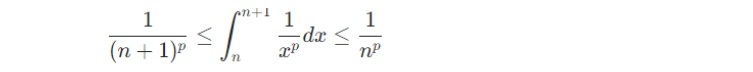
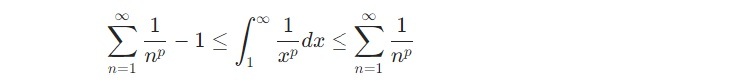
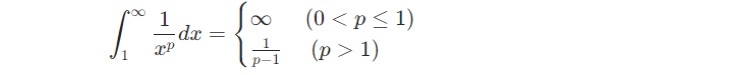

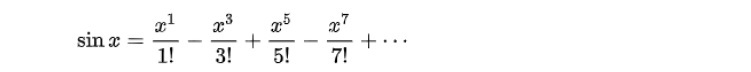
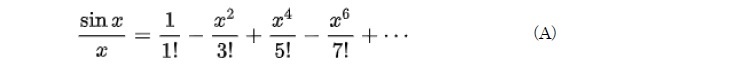
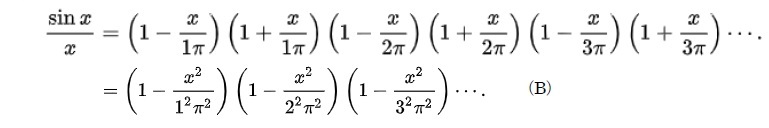
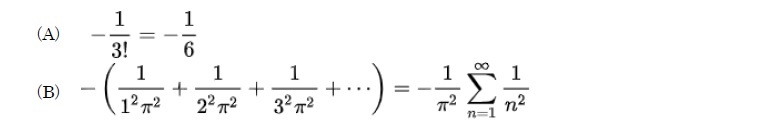

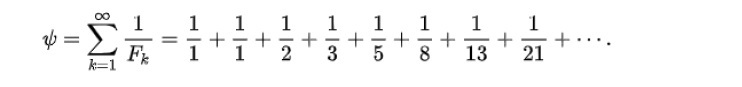

 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




