- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 「三角関数」と「波」の関係(その2)-電波によるデータ送信の仕組みと三角関数による「波」の表現の利用-
コラム
2021年08月27日
文字サイズ
- 小
- 中
- 大
周波数の変調
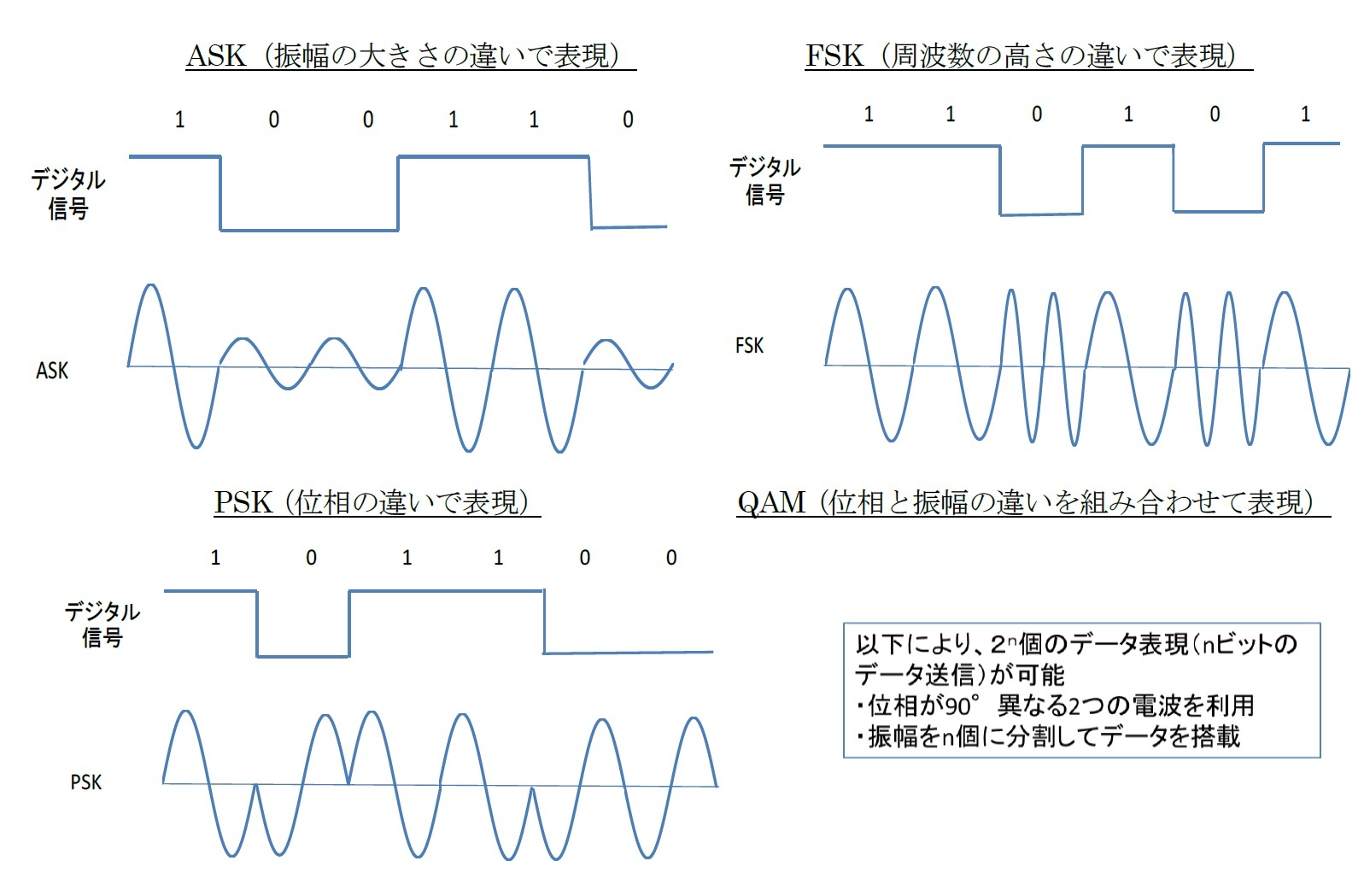
デジタル信号の場合の「変調」には、ASK(amplitude shift keying :振幅変異変調)、FSK(frequency shift keying:周波数偏移変調)、PSK(phase shift keying:位相偏移変調)及びQAM(quadrature amplitude modulation:直角位相振幅変調)等がある5。
その基本的な考え方は、以下の図の通りとなる。
なお、QAMは、位相が90°異なる(直交する)2つの電波の振幅の組み合わせにデータを割り当てる方式であり、下記の図では振幅を4つの大きさに区分することで、16種類のデータの表現が可能になる(即ち、4ビット(4桁)のデジタル信号を一度に送ることができることになる。これを16QAM(16=24)という。
なお、現在の4G通信は64QAMが使用され、一度に送れるデータ量は6ビットだが、5G通信では256QAMが使用され、一度に8ビットのデータを伝送することができることになる。
その基本的な考え方は、以下の図の通りとなる。
なお、QAMは、位相が90°異なる(直交する)2つの電波の振幅の組み合わせにデータを割り当てる方式であり、下記の図では振幅を4つの大きさに区分することで、16種類のデータの表現が可能になる(即ち、4ビット(4桁)のデジタル信号を一度に送ることができることになる。これを16QAM(16=24)という。
なお、現在の4G通信は64QAMが使用され、一度に送れるデータ量は6ビットだが、5G通信では256QAMが使用され、一度に8ビットのデータを伝送することができることになる。
5 デジタル通信の元祖のようなものともいえる「モールス信号」で、変調状態と無変調状態を電鍵(Key)で切り替えていたことから、変調に対して、「modulation」でなく、「Keying」という用語が使用されてきている。
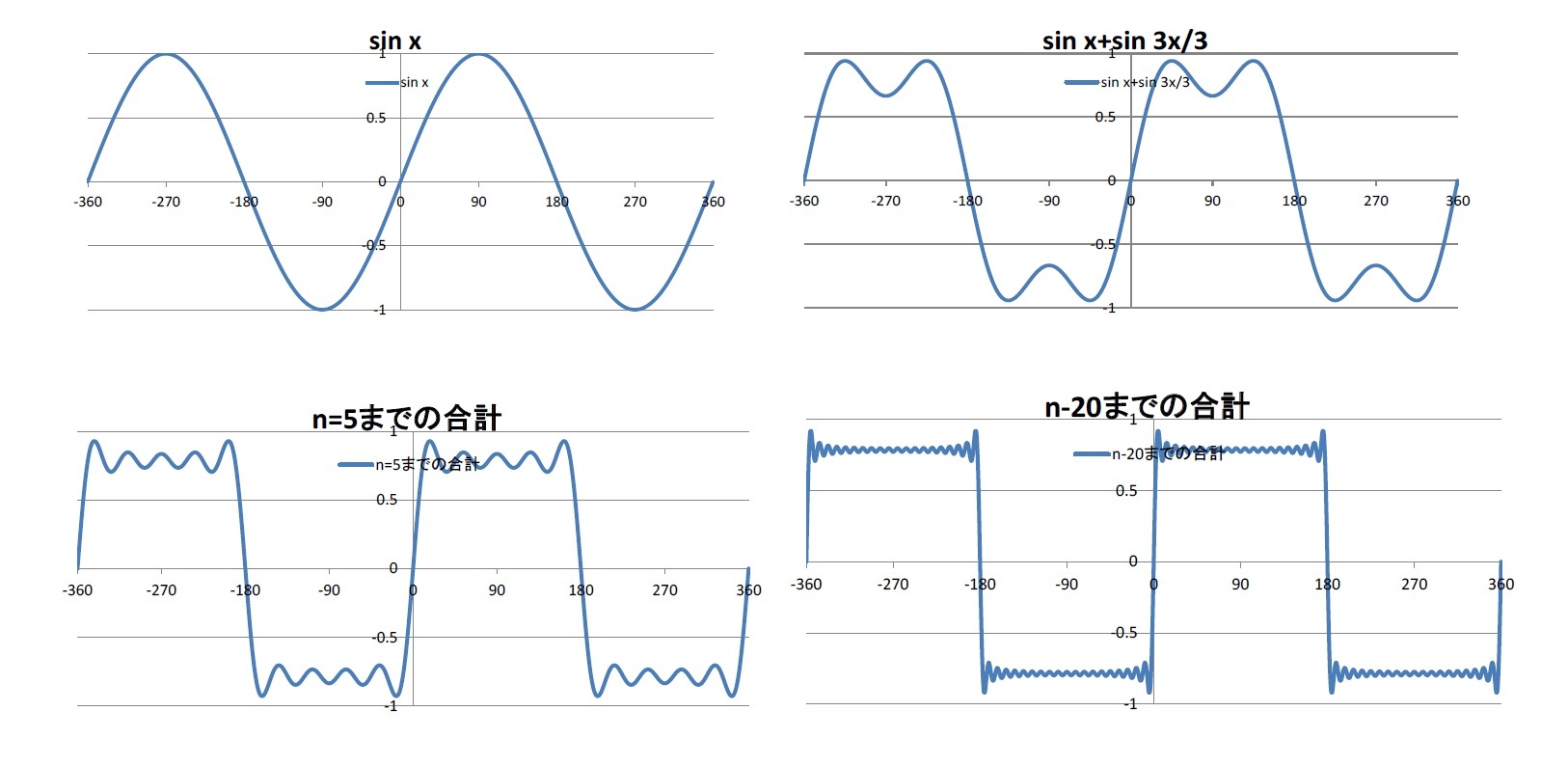
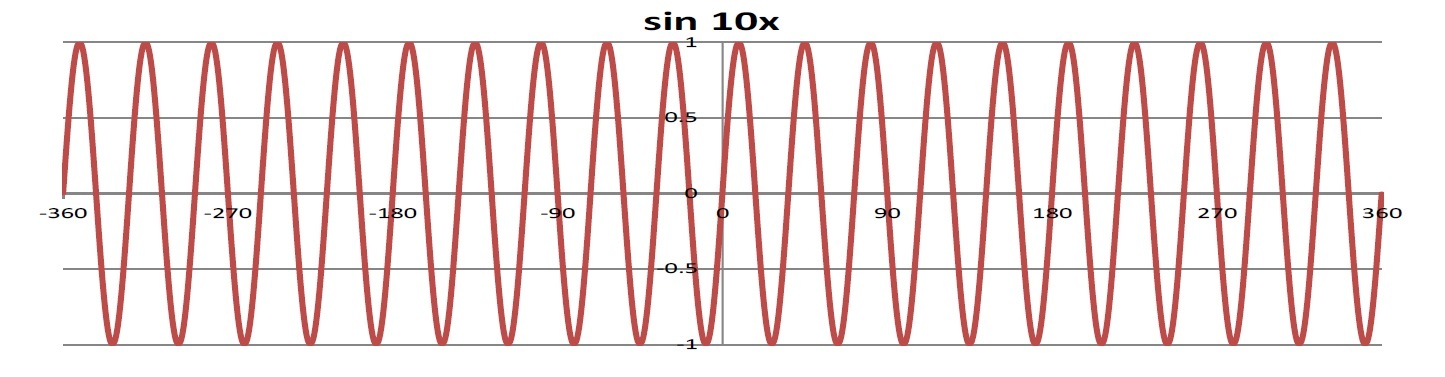
代表的な波形の三角関数による表現
このように複雑な波も、周波数の異なる正弦波で表現することができることになると、各種の信号やデータ等の情報を変調して送信し、復調して受信することができることになる。
また、音波については、オーケストラによる演奏、街並みの喧騒等の様々な音は全て、正弦波の和で表すことができ、これらをCD等に録音し、再生するというような情報の保存・再現が可能になる。
さらに、光波(赤外線、可視光、紫外線)の分析を行うことで色の解析を行うことができる。加えて、地震波の分析を行うことで震源過程の解析や地震波による建物への影響分析等を行うこともできることになる。
また、音波については、オーケストラによる演奏、街並みの喧騒等の様々な音は全て、正弦波の和で表すことができ、これらをCD等に録音し、再生するというような情報の保存・再現が可能になる。
さらに、光波(赤外線、可視光、紫外線)の分析を行うことで色の解析を行うことができる。加えて、地震波の分析を行うことで震源過程の解析や地震波による建物への影響分析等を行うこともできることになる。
携帯電話の仕組み
携帯電話は、先に述べたような仕組みの中で、人の声をアナログ信号からデジタル信号に変換して、邪魔になるエコーやノイズを除去して音質を良くしたものを、伝送しやすいように圧縮して送信している。受信サイドは、音声を復元して、聞き取りやすい音声に加工した後、デジタル信号をアナログ信号に変換することで、人の声を再現している。
この携帯電話の仕組みが機能する過程では、各種の場面で三角関数に基づいたテクニックが使用されている。
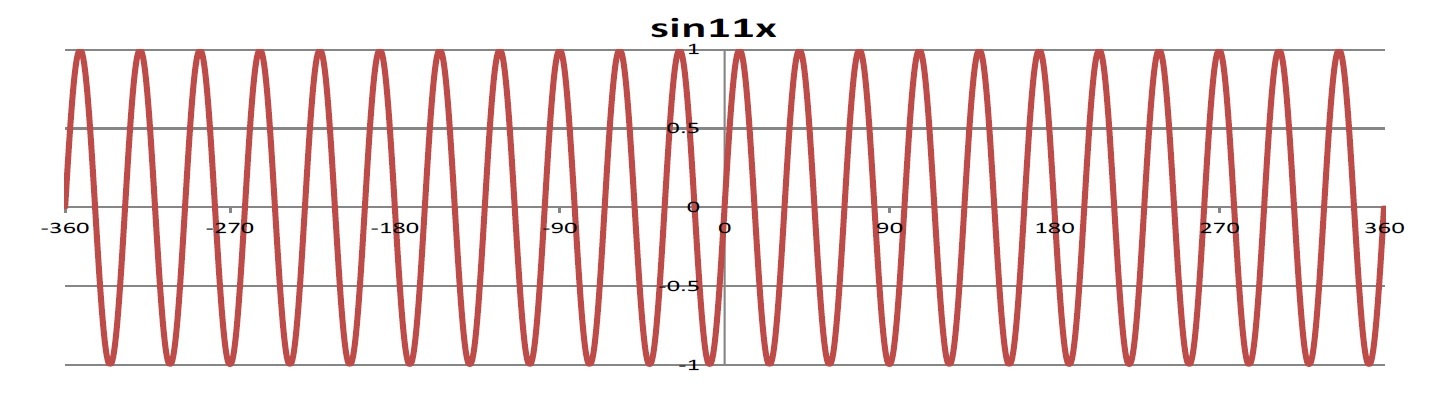
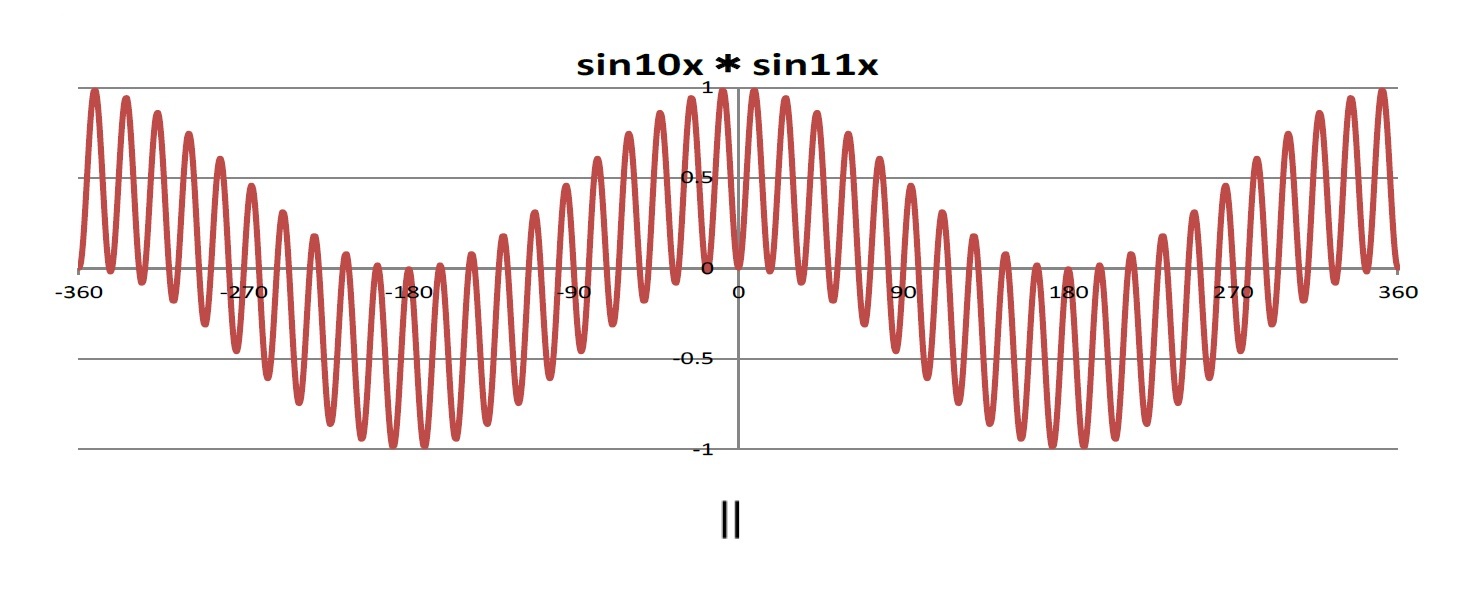
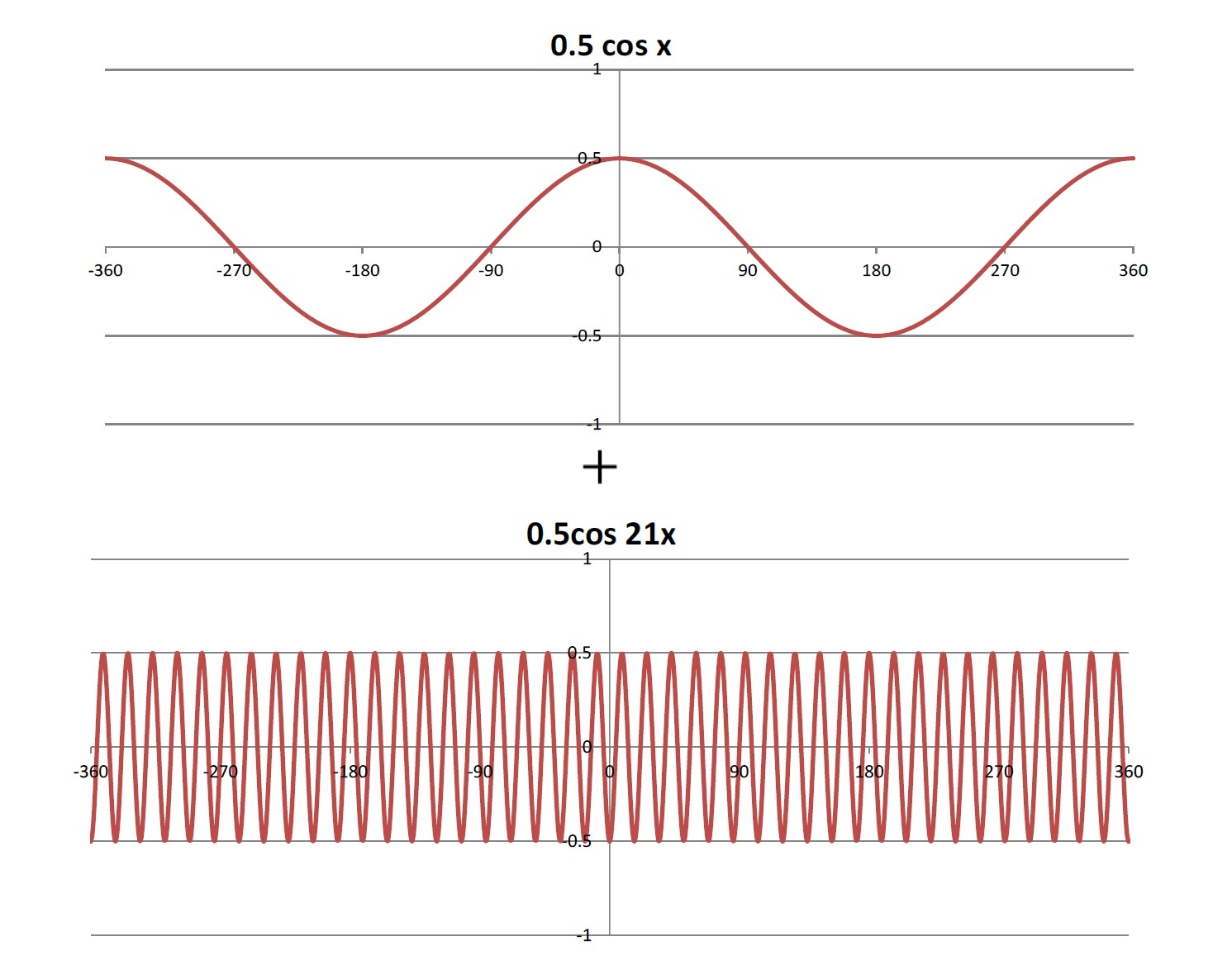
例えば、この三角関数のシリーズの前々回の研究員の眼で紹介した以下のような「三角関数の積和公式」を用いて、周波数が異なる2つの波を掛け合わせることで、元の2つとは異なる周波数の波を得ること(周波数転換)が行われる。
sinα・sinβ=-{cos(α+β)-cos(α-β)}/2
携帯電話の電波には700MHzから4.5GHz程度の周波数が使用されているが、これらは携帯電話の内部で扱うにはかなり高い周波数となるため、携帯電話では外部から受信した高い周波数の電波を内部で変換して、より低い周波数で信号処理することが行われる。具体的には、以下の例のように、受信した電波と同程度の周波数の波を掛け合わせることで、より低い周波数の波を作り出している。
外部から受信した電波
この携帯電話の仕組みが機能する過程では、各種の場面で三角関数に基づいたテクニックが使用されている。
例えば、この三角関数のシリーズの前々回の研究員の眼で紹介した以下のような「三角関数の積和公式」を用いて、周波数が異なる2つの波を掛け合わせることで、元の2つとは異なる周波数の波を得ること(周波数転換)が行われる。
sinα・sinβ=-{cos(α+β)-cos(α-β)}/2
携帯電話の電波には700MHzから4.5GHz程度の周波数が使用されているが、これらは携帯電話の内部で扱うにはかなり高い周波数となるため、携帯電話では外部から受信した高い周波数の電波を内部で変換して、より低い周波数で信号処理することが行われる。具体的には、以下の例のように、受信した電波と同程度の周波数の波を掛け合わせることで、より低い周波数の波を作り出している。
外部から受信した電波
さらには、携帯電話中の話し手の声以外の各種の外部からの雑音がある場合に、これらの雑音と話し手の声が一体になった音波を(先に述べたフーリエによる手法で)各種の正弦波に分解することで、雑音に相当する部分を除去することができることになる。
まとめ
以上、今回の研究員の眼では、三角関数によって、波が表現されることで、どのように社会で役立っているのかについて、具体的に電波によって、どのように情報が送信されていくのかを例にして、その簡単な仕組みや原理を報告してきた。
三角関数シリーズの次回の研究員の眼では、まさに今回の研究員の眼でも触れた、複雑な波を単純な波に分解する数学的手法である「フーリエ級数展開」や「フーリエ変換」について、報告する。
三角関数シリーズの次回の研究員の眼では、まさに今回の研究員の眼でも触れた、複雑な波を単純な波に分解する数学的手法である「フーリエ級数展開」や「フーリエ変換」について、報告する。
(2021年08月27日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
新着記事
-
2025年10月28日
試練の5年に踏み出す中国(前編)-「第15次五カ年計画」の5年間は、どのような5年か -
2025年10月28日
地域医療連携推進法人の現状と今後を考える-「連携以上、統合未満」で協力する形態、その将来像は? -
2025年10月28日
東宝の自己株式取得-公開買付による取得 -
2025年10月28日
今週のレポート・コラムまとめ【10/21-10/27発行分】 -
2025年10月27日
大学卒女性の働き方別生涯賃金の推計(令和6年調査より)-正社員で2人出産・育休・時短で2億円超
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【「三角関数」と「波」の関係(その2)-電波によるデータ送信の仕組みと三角関数による「波」の表現の利用-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
「三角関数」と「波」の関係(その2)-電波によるデータ送信の仕組みと三角関数による「波」の表現の利用-のレポート Topへ




















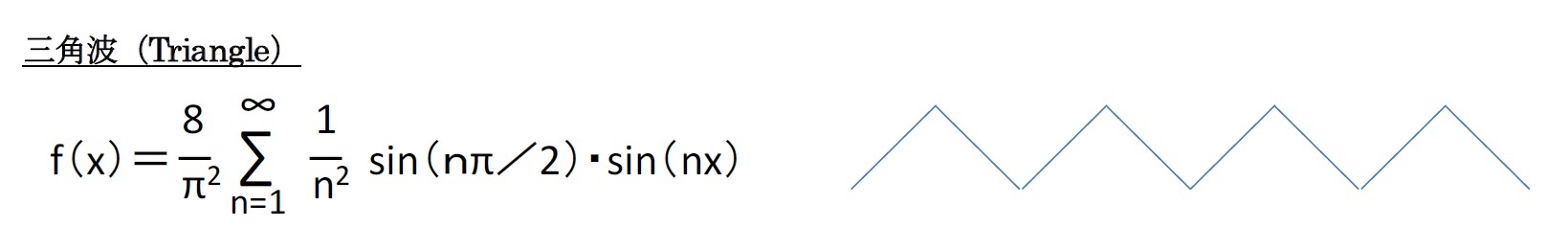

 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




