- シンクタンクならニッセイ基礎研究所 >
- 経済 >
- 経済予測・経済見通し >
- 統計分析を理解しよう:正規分布、標準化、標準正規分布の概念
文字サイズ
- 小
- 中
- 大
正規分布とは?
一方、連続確率分布とは、あるクラスにおける学生の体重、身長など、数値そのものに意味があり、四則演算ができるデータ(このようなデータを「量的データ」あるいは「連続データ」という)で、確率変数が連続的な場合の確率分布である1。そして、連続確率分布をグラフで描いたものが確率密度関数である。確率密度関数は図表1のように多様な形があり得るものの、Cのように真ん中に山が来て左右対称の形をしているのが「正規分布」の一般的な形である。
(1) -∞~∞の実数値をとる。
(2) 山が一つで平均値(
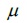 、以下、平均)付近の確率密度が最も大きく、平均と中央値、最頻値が一致する。
、以下、平均)付近の確率密度が最も大きく、平均と中央値、最頻値が一致する。(3) 平均を中心として左右対称の釣鐘型の分布である。
(4) 平均から離れるほど、確率密度が小さくなる。
(5) 正規分布のカーブの下の面積は形にかかわらず、どれも”1”になっており、分布のカーブの下の面積は確率を示している。
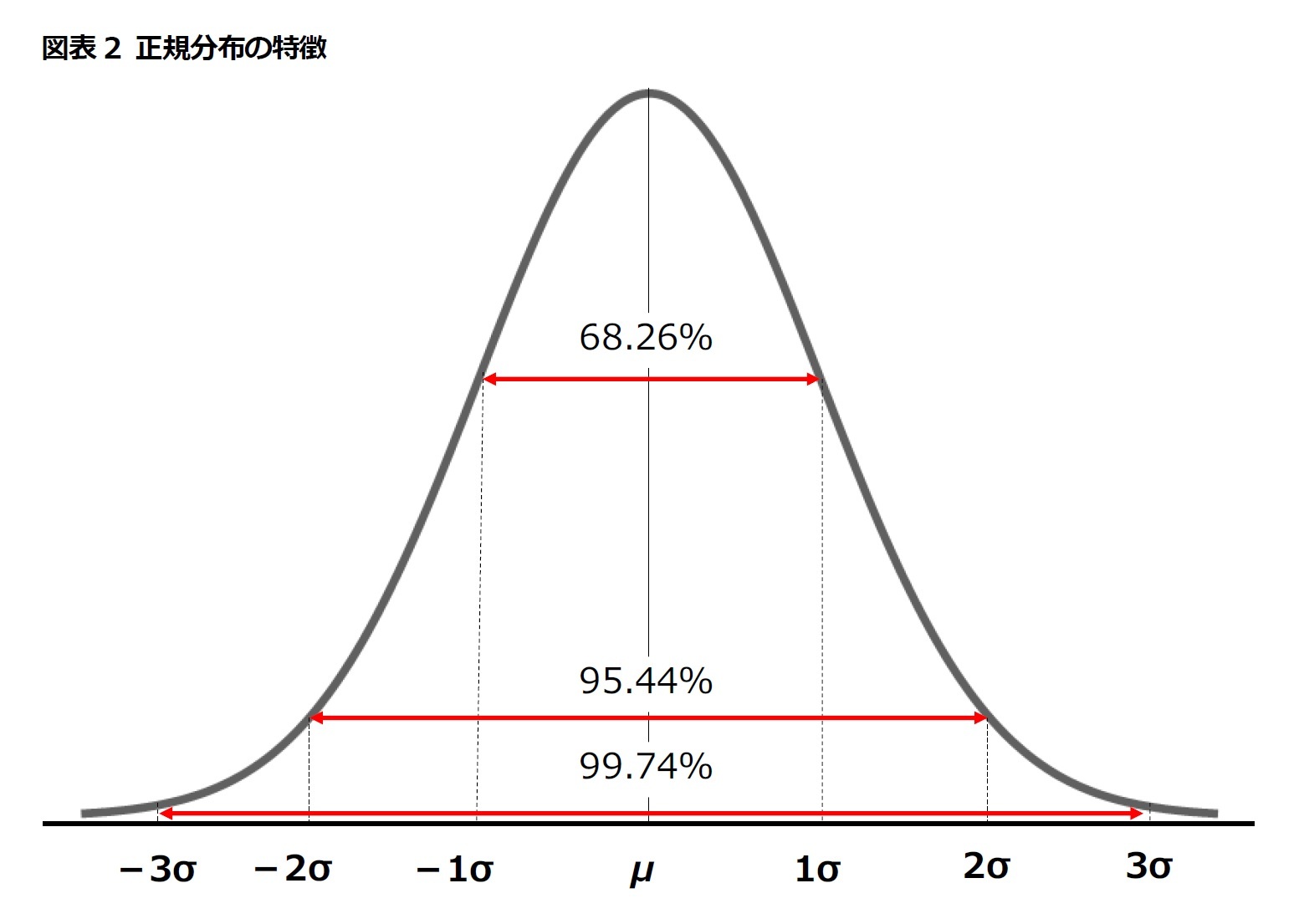
つまり、
⇒ 平均から左右に標準偏差1つ分(平均(
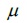 )±標準偏差(
)±標準偏差(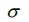 )×1)の区間にデータが入る確率は68.26%
)×1)の区間にデータが入る確率は68.26%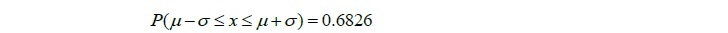
⇒ 平均から左右に標準偏差2つ分(平均(
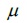 )±標準偏差(
)±標準偏差(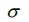 )×2)の区間にデータが入る確率は95.44%
)×2)の区間にデータが入る確率は95.44%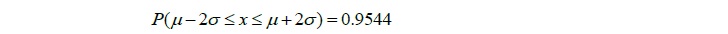
⇒ 平均から左右に標準偏差3つ分(平均(
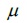 )±標準偏差(
)±標準偏差(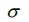 )×3)の区間にデータが入る確率は99.74%
)×3)の区間にデータが入る確率は99.74%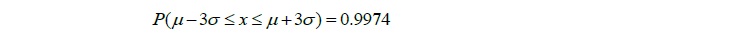
である(図表2)。
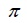 は3.14159…、eは2.71828…という値がすでに決まっているので、平均(
は3.14159…、eは2.71828…という値がすでに決まっているので、平均(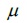 )と標準偏差(
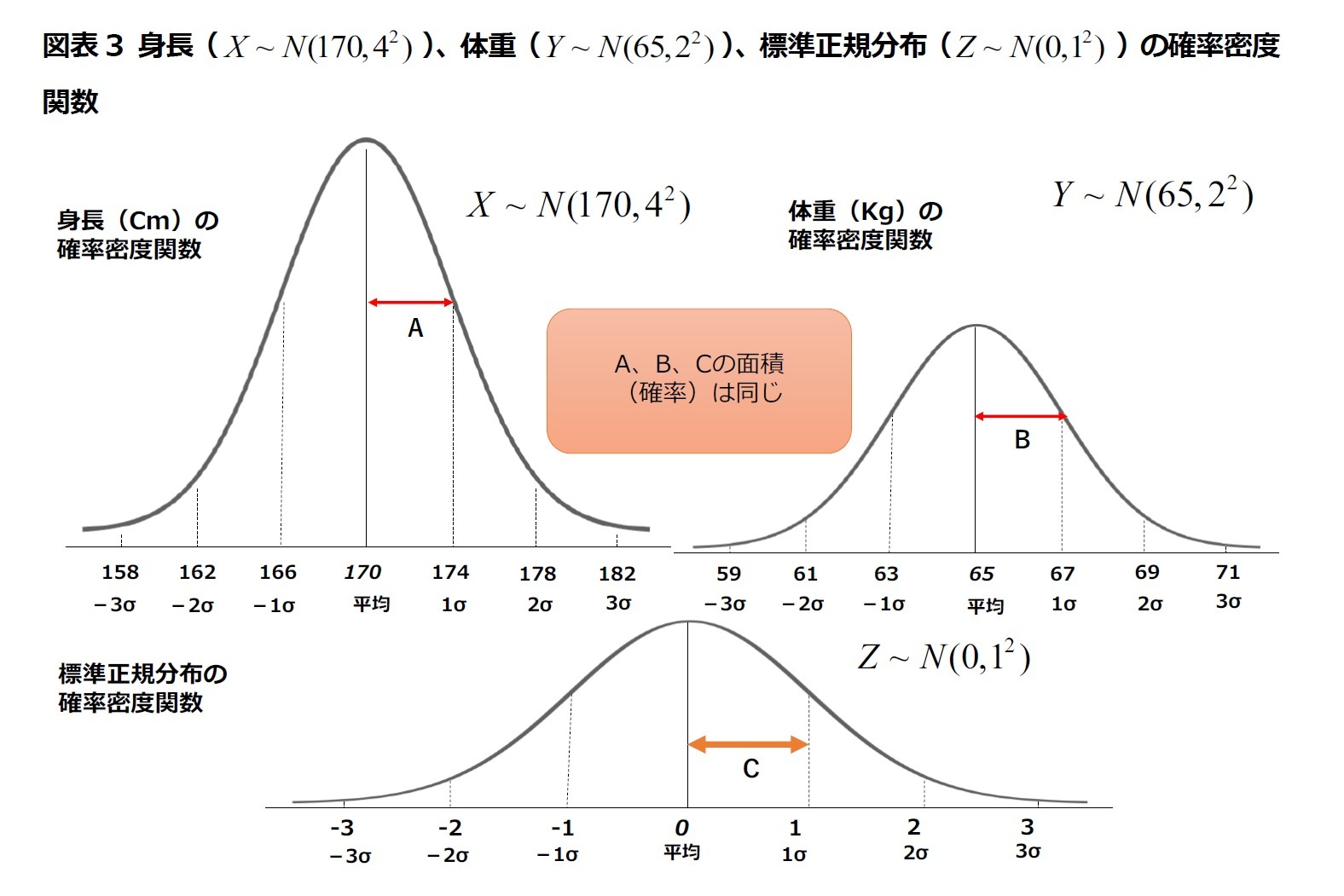
)と標準偏差(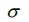 )さえ分かれば正規分布の形が決まることになる。つまり、平均は確率密度関数のグラフの位置を決め、標準偏差はグラフの形を決定する。標準偏差が小さいと、平均付近にデータが集まり、標準偏差が大きいと、データが平均から大きく離れることになる。
)さえ分かれば正規分布の形が決まることになる。つまり、平均は確率密度関数のグラフの位置を決め、標準偏差はグラフの形を決定する。標準偏差が小さいと、平均付近にデータが集まり、標準偏差が大きいと、データが平均から大きく離れることになる。
1 変数(variables、変量とも言う)とは、調査対象により異なり、ある調査を行って得られた結果(データ)に名前を付けたものである。また、確率変数とは、標本空間にある全ての要素を実数に対応させたものだと言える。
標準化と標準正規分布
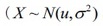 と仮定できる場合、このデータを標準化した「標準正規分布表」を用いて一定区間の確率(面積)を求める方法が利用されている。
と仮定できる場合、このデータを標準化した「標準正規分布表」を用いて一定区間の確率(面積)を求める方法が利用されている。標準化とは、世の中の無数の確率変数が同じ平均と標準偏差を持つように確率変数を変換することである。確率変数
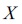 を標準化するには、該当する値(
を標準化するには、該当する値(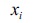 )から平均(
)から平均(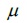 )を引き、標準偏差(
)を引き、標準偏差(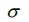 )で割ればよい。すると、確率変数は標準化確率変数に変わり、確率変数の単位に関係なく平均0、標準偏差1の値を持つことになる。標準化した
)で割ればよい。すると、確率変数は標準化確率変数に変わり、確率変数の単位に関係なく平均0、標準偏差1の値を持つことになる。標準化した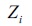 は、ある値
は、ある値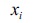 が平均から離れた距離が標準偏差の何倍であるかを意味する。
が平均から離れた距離が標準偏差の何倍であるかを意味する。
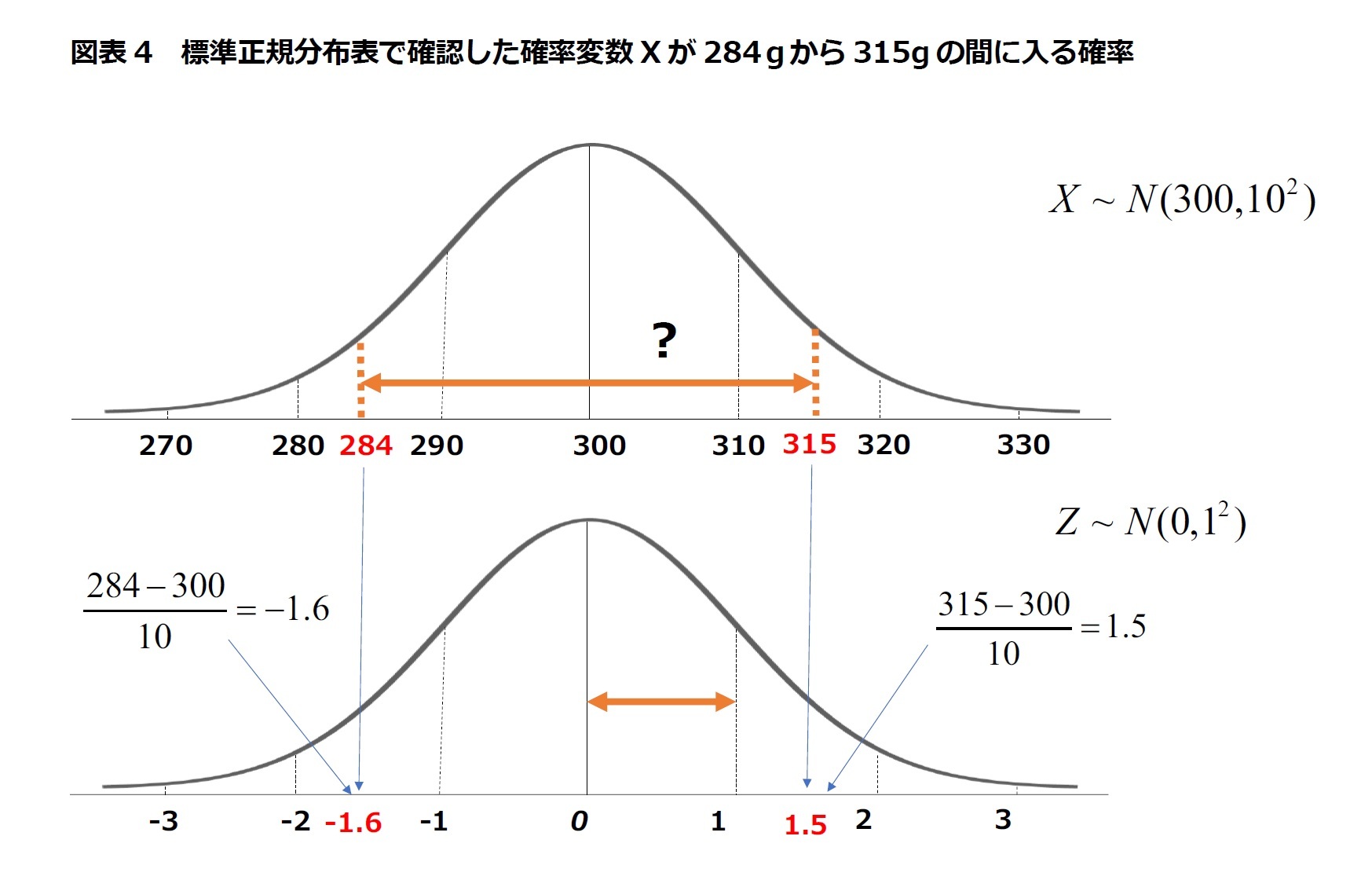
まず、式(5)を利用して284gと315gを標準化すると、標準化した値はそれぞれ-1.6と1.5になる。つまり、確率変数
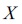 が284gから315gの間に入る確率と、標準正規分布の変数である
が284gから315gの間に入る確率と、標準正規分布の変数である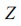 が-1.6と1.5の間に入る確率は同じである(図表4)。また、標準正規分布の確率密度関数は左右対称であるので、
が-1.6と1.5の間に入る確率は同じである(図表4)。また、標準正規分布の確率密度関数は左右対称であるので、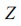 の値が0から-1.6の間に入る確率は、
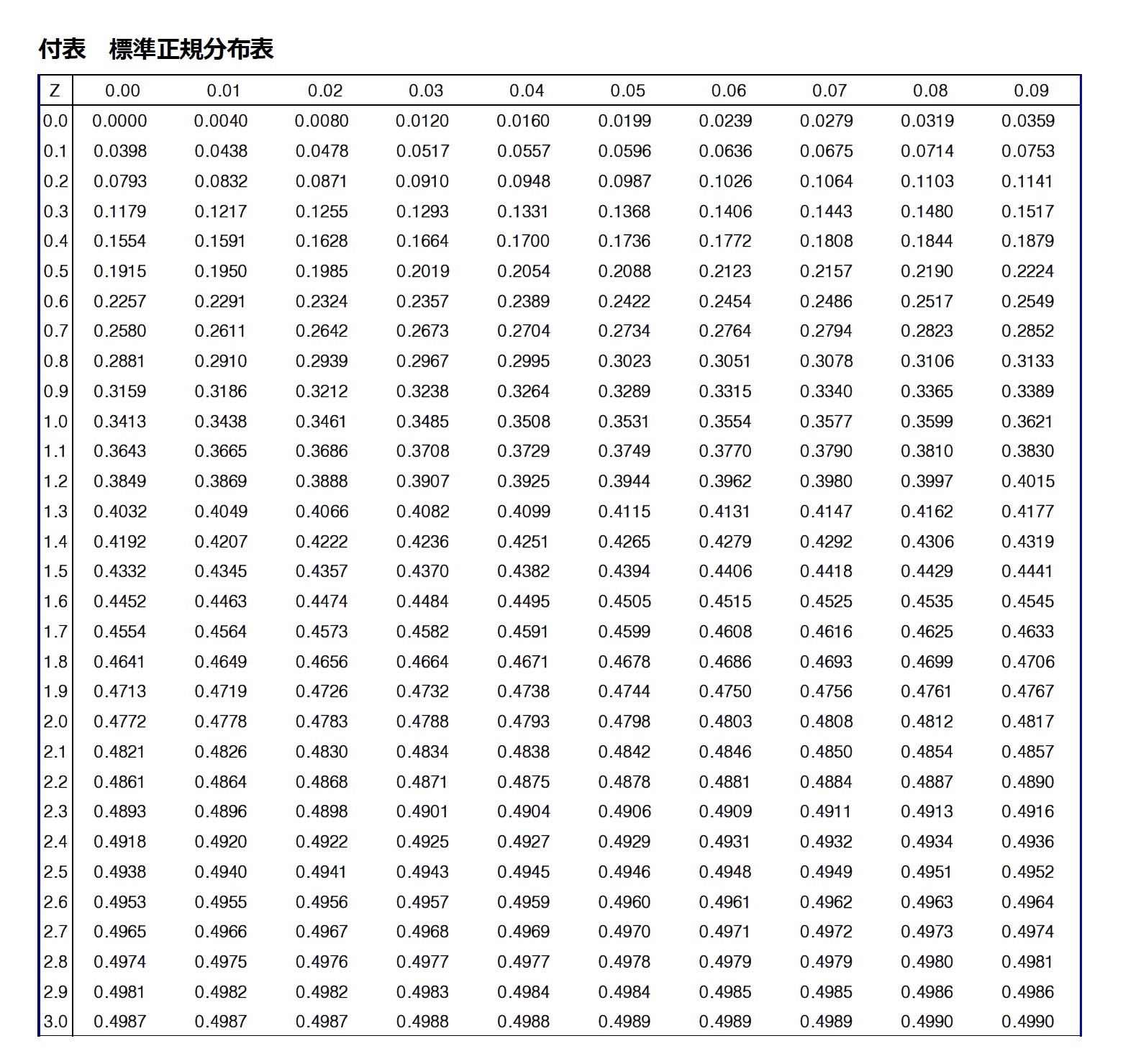
の値が0から-1.6の間に入る確率は、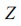 の値が0から1.6の間に入る確率を標準正規分布表から確認すればよい(式(6))。そこで、標準正規分布表を利用してその確率を求めると、確率変数
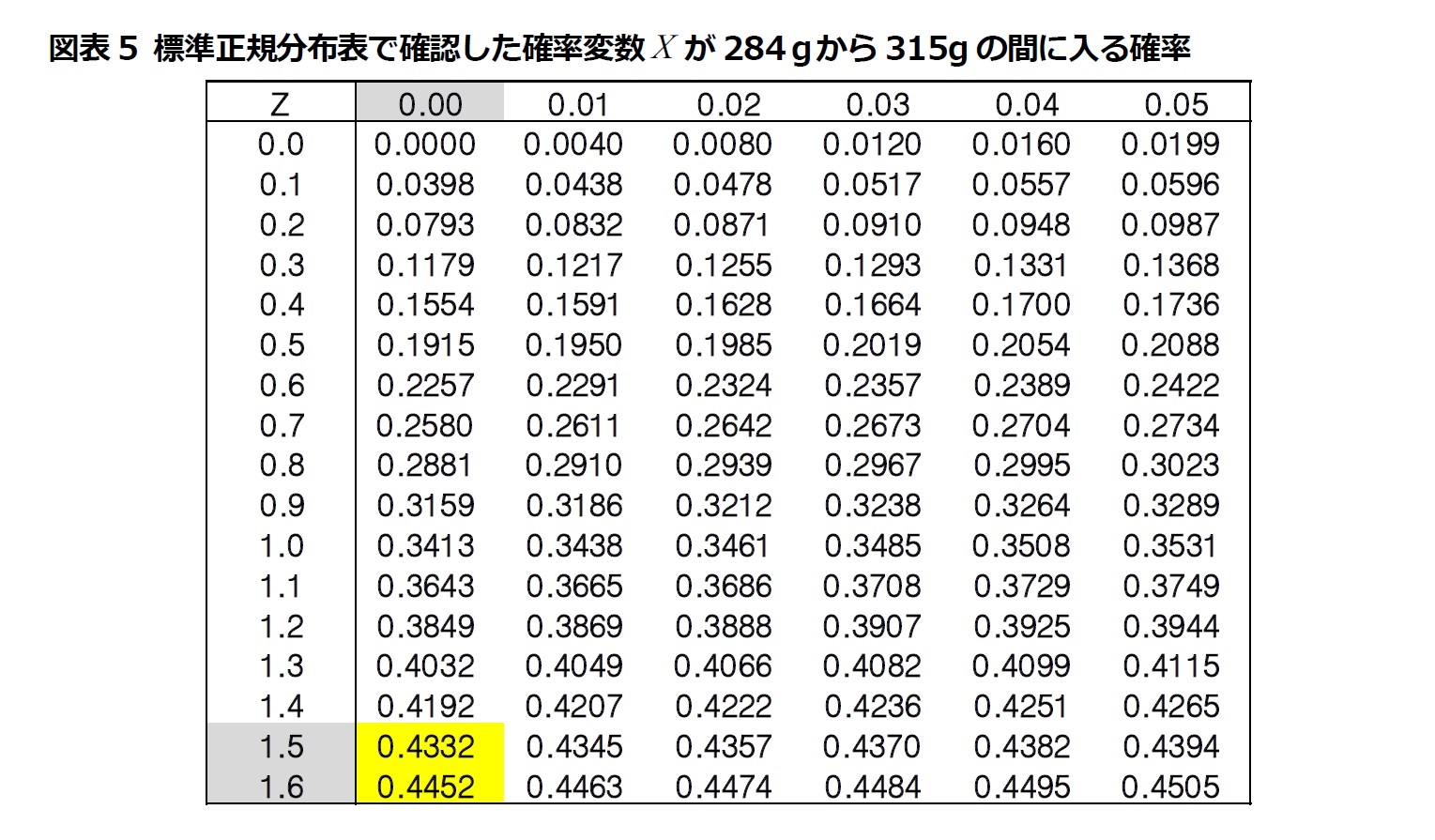
の値が0から1.6の間に入る確率を標準正規分布表から確認すればよい(式(6))。そこで、標準正規分布表を利用してその確率を求めると、確率変数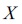 が284gから315gの間に入る確率は、87.84%(0.4452+0.4332=0.8784)であることが分かる(図表5)。
が284gから315gの間に入る確率は、87.84%(0.4452+0.4332=0.8784)であることが分かる(図表5)。本資料記載のデータは各種の情報源から入手・加工したものであり、その正確性と完全性を保証するものではありません。
また、本資料は情報提供が目的であり、記載の意見や予測は、いかなる契約の締結や解約を勧誘するものではありません。
(2021年01月19日「研究員の眼」)
このレポートの関連カテゴリ

生活研究部 上席研究員・ヘルスケアリサーチセンター・ジェロントロジー推進室兼任
金 明中 (きむ みょんじゅん)
研究・専門分野
高齢者雇用、不安定労働、働き方改革、貧困・格差、日韓社会政策比較、日韓経済比較、人的資源管理、基礎統計
03-3512-1825
- プロフィール
【職歴】
独立行政法人労働政策研究・研修機構アシスタント・フェロー、日本経済研究センター研究員を経て、2008年9月ニッセイ基礎研究所へ、2023年7月から現職
・2011年~ 日本女子大学非常勤講師
・2015年~ 日本女子大学現代女性キャリア研究所特任研究員
・2021年~ 横浜市立大学非常勤講師
・2021年~ 専修大学非常勤講師
・2021年~ 日本大学非常勤講師
・2022年~ 亜細亜大学都市創造学部特任准教授
・2022年~ 慶應義塾大学非常勤講師
・2019年 労働政策研究会議準備委員会準備委員
東アジア経済経営学会理事
・2021年 第36回韓日経済経営国際学術大会準備委員会準備委員
【加入団体等】
・日本経済学会
・日本労務学会
・社会政策学会
・日本労使関係研究協会
・東アジア経済経営学会
・現代韓国朝鮮学会
・博士(慶應義塾大学、商学)
金 明中のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/07/08 | 「静かな退職」と「カタツムリ女子」の台頭-ハッスルカルチャーからの脱却と新しい働き方のかたち | 金 明中 | 基礎研マンスリー |
| 2025/06/06 | “サヨナラ”もプロに任せる時代-急増する退職代行サービス利用の背景とは? | 金 明中 | 基礎研マンスリー |
| 2025/06/02 | 日韓カップルの増加は少子化に歯止めをかけるか? | 金 明中 | 研究員の眼 |
| 2025/05/22 | 【アジア・新興国】韓国の生命保険市場の現状-2023年のデータを中心に- | 金 明中 | 保険・年金フォーカス |
新着記事
-
2025年10月30日
潜在成長率は変えられる-日本経済の本当の可能性 -
2025年10月30日
米FOMC(25年10月)-市場予想通り、政策金利を▲0.25%引き下げ。バランスシート縮小を12月1日で終了することも決定 -
2025年10月30日
試練の5年に踏み出す中国(後編)-「第15次五カ年計画」建議にみる、中国のこれからの針路 -
2025年10月30日
米国で進む中間期の選挙区割り変更-26年の中間選挙を見据え、与野党の攻防が激化 -
2025年10月29日
生活習慣病リスクを高める飲酒の現状と改善に向けた対策~男女の飲酒習慣の違いに着目して
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【統計分析を理解しよう:正規分布、標準化、標準正規分布の概念】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
統計分析を理解しよう:正規分布、標準化、標準正規分布の概念のレポート Topへ

















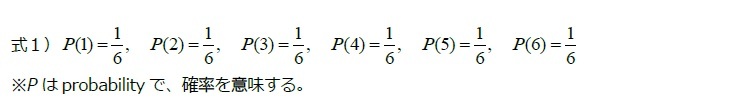
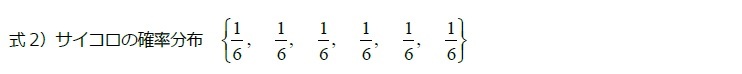
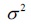 の正規分布に従うとき(式(3))、その確率密度関数は式(4)のようになる。
の正規分布に従うとき(式(3))、その確率密度関数は式(4)のようになる。


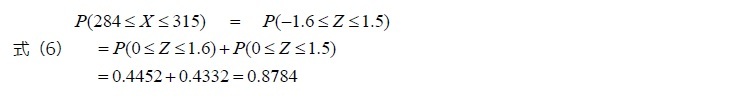

 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




