- シンクタンクならニッセイ基礎研究所 >
- 経済 >
- 経済予測・経済見通し >
- 統計分析を理解しよう-ロジスティック回帰分析の概要-
文字サイズ
- 小
- 中
- 大
ロジスティック回帰分析とは
このように被説明変数が質的データであっても分析ができるよう一般線形モデルを拡張したのが一般化線形モデル(GLM:Generalized Linear Model)である。一般線形モデルが、被説明変数が正規分布をしている時のみを扱っていることに比べて、一般化線形モデルは、正規分布以外の分布(二項分布、ポアソン分布等)に従う被説明変数を予測する時にも使われる。また、一般線形モデルでは被説明変数と説明変数の線形的な関係を推計することに対して、一般化線形モデルは2値変数を扱えるようにするために被説明変数を適切な関数に変えたf(x)と説明変数の関係を推計する。このような一般化線形モデルで最も使われている分析方法がロジスティック分析である。
被説明変数が2値変数である場合には二項ロジスティック分析を、3項(カテゴリー)以上の場合は多項ロジスティック分析を、そして、順序変数である場合には順序ロジスティック分析を行う。
1 回帰分析の概要については、金 明中(2018)「回帰分析を理解しよう!-回帰分析の由来と概念、そして分析結果の評価について-」研究員の眼 、2018年5月16日を参照すること。
1 量的データとは、データの連続性があり、足したり引いたり演算ができ、演算しても数値として意味のあるデータである。一方、質的データは、分類や種類を区別するためのデータ(性別、学歴カテゴリ、地域カテゴリ等)であり、そのまま足したり引いたり演算ができず演算をしても意味のないデータである。
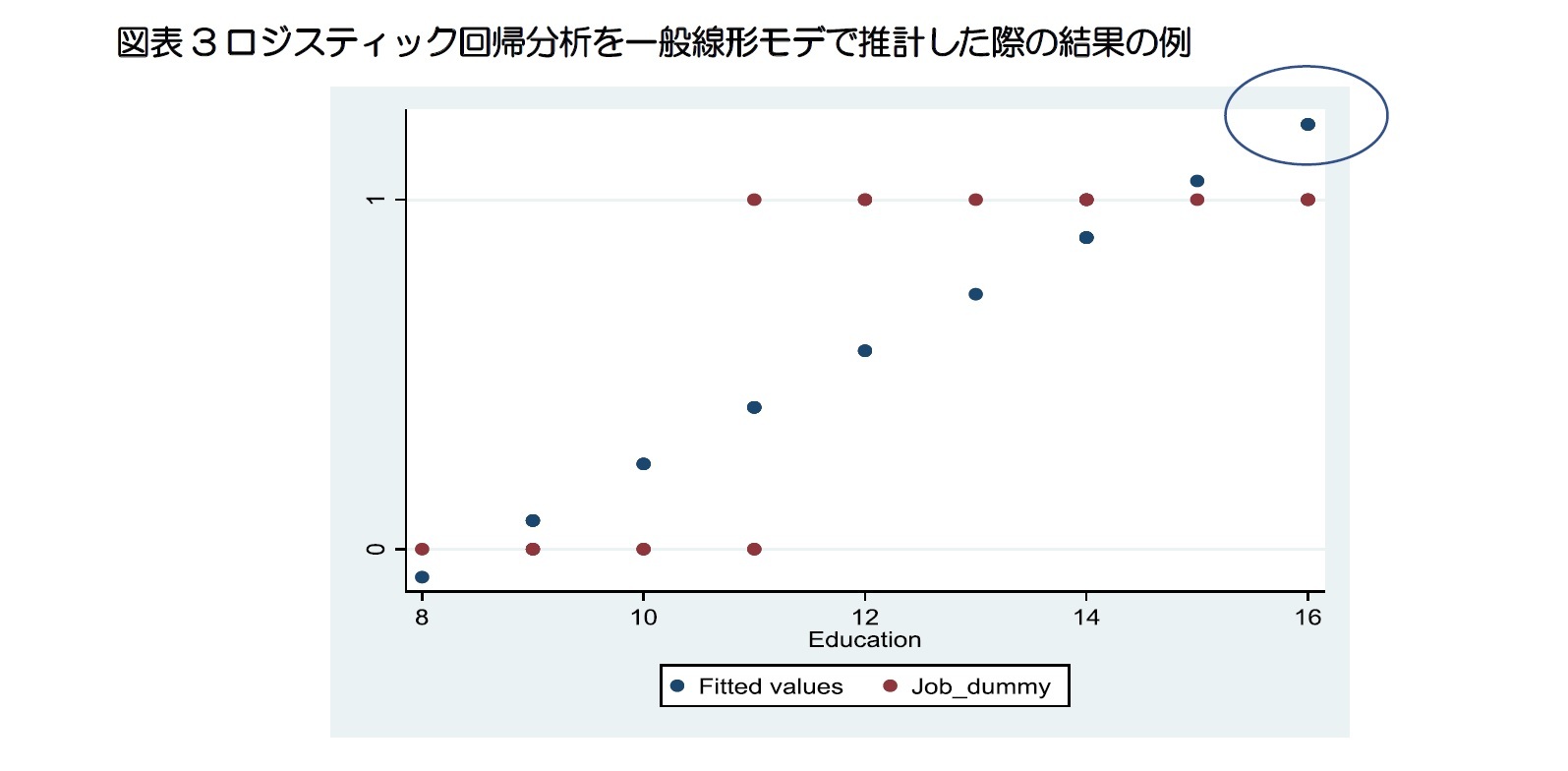
質的データを一般線形モデルで推計する誤り
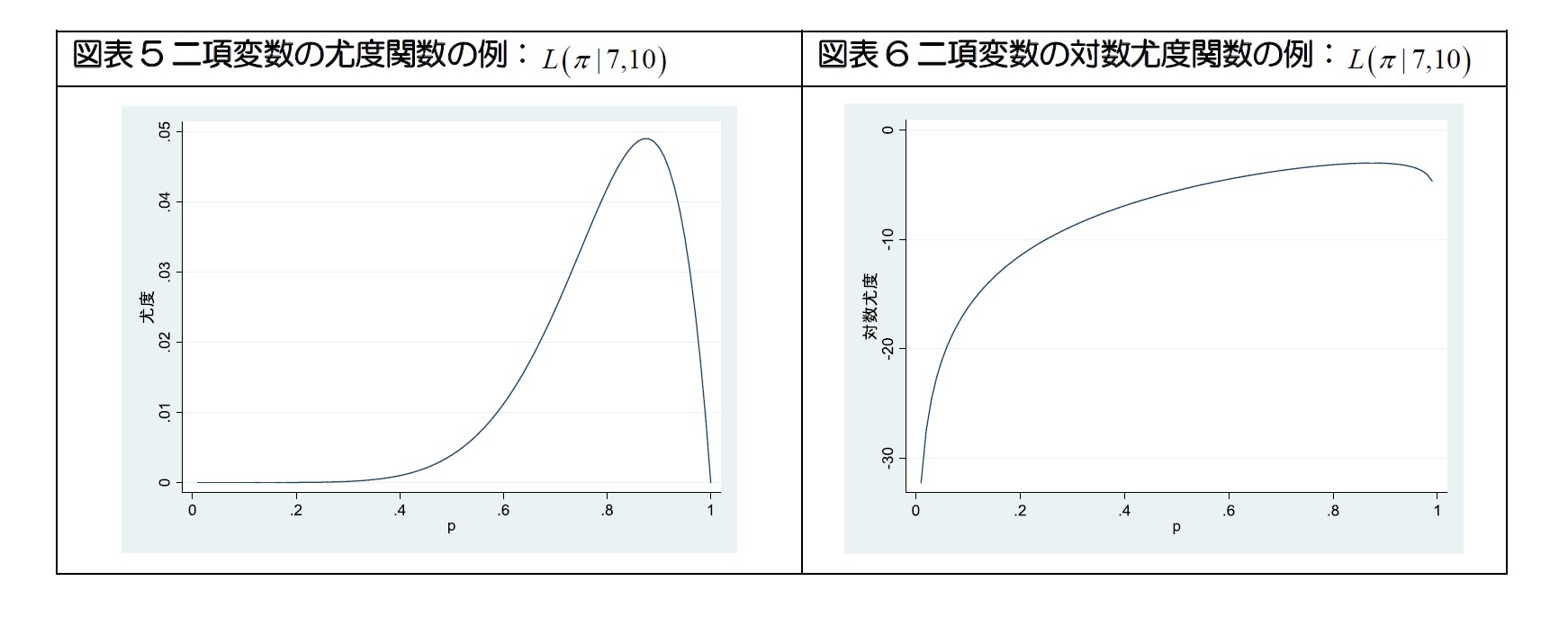
山澤(2004)は「尤度とは、同時確率密度関数の解釈を変えたものである。確率密度関数は、確率変数がどの程度の確率で表れるかを関数にしたもので、同時確率密度関数は、複数の確率変数が同時に起こる確率である」と説明している。
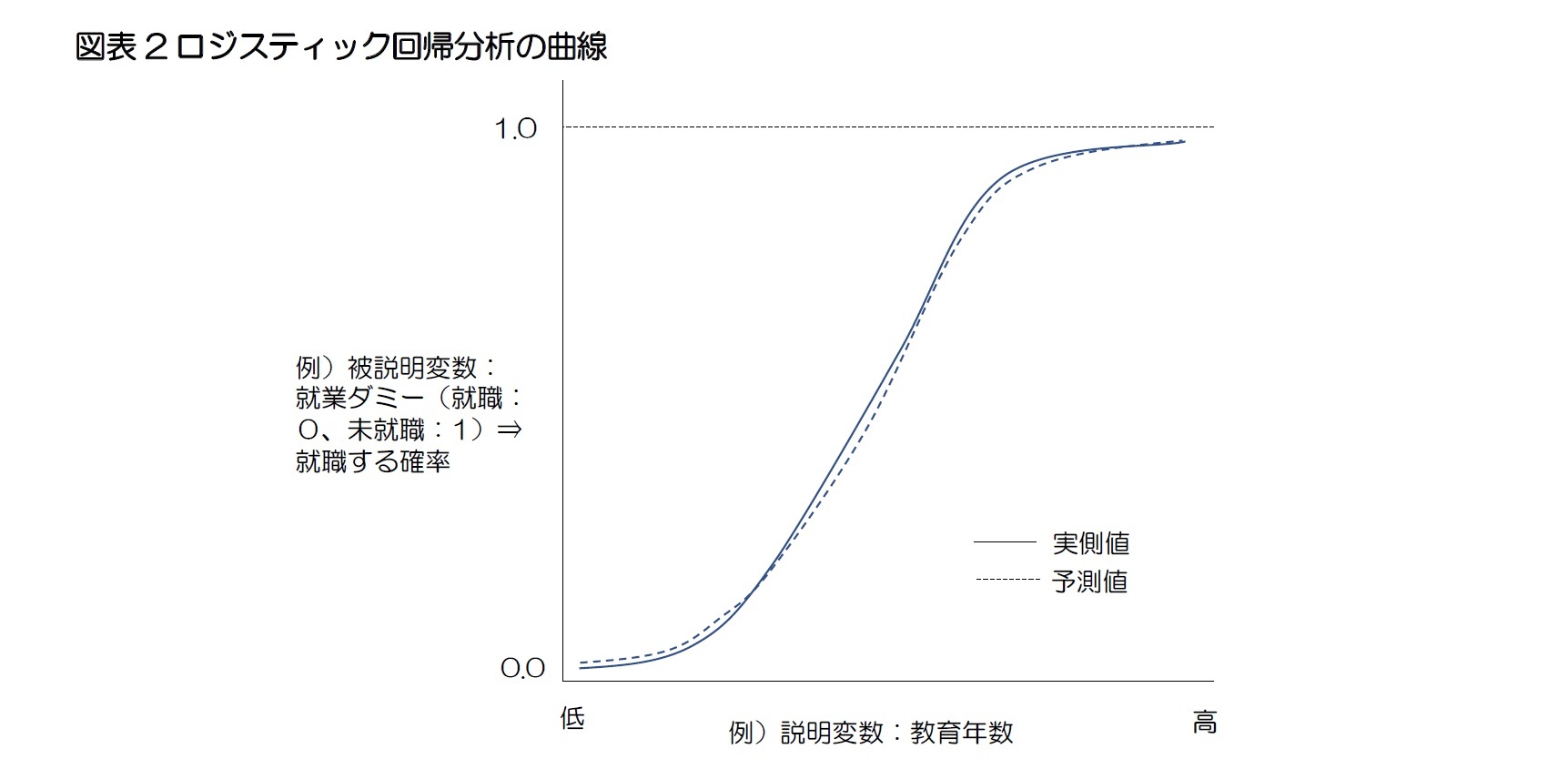
ロジスティック分析は、ある事件(event)が発生するかしないかを直接予測することではなく、その事件が発生する確率を予測する。従って、被説明変数の値は0と1の間の数値になる。分析結果、被説明変数の値、すなわち確率が0.5より大きいとその事件が発生すると予測し、0.5を下回るとその事件が発生しないと予測する。ロジスティック分析における説明変数と非説明変数との関係を示すと図表2のようなS字形の曲線になる。
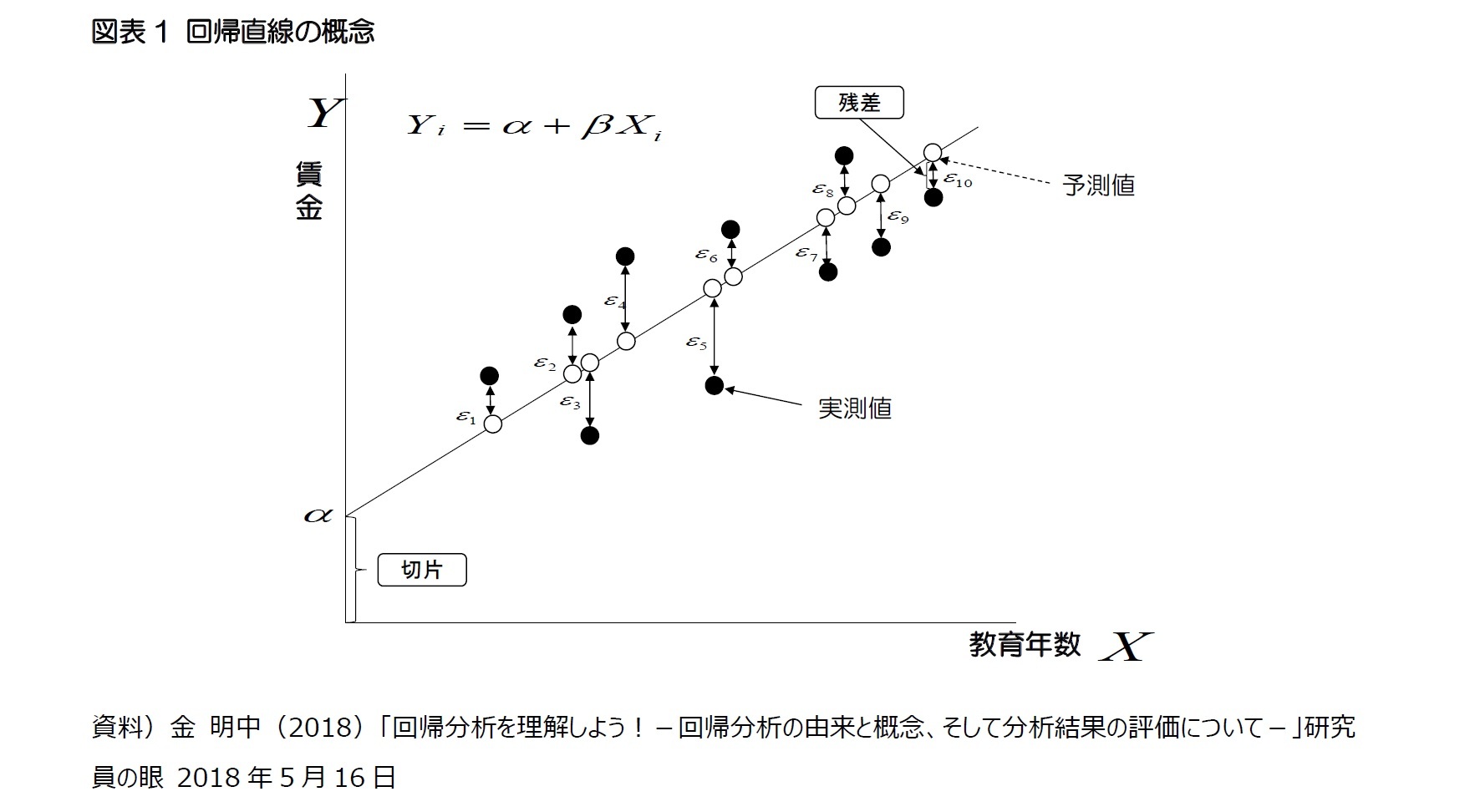
3 「誤差」は、母集団の真の回帰式から算出される値(真値)と実際に測定された値(実測値)との差を表す。一方、「残差」は標本集団のデータを用いて推計された回帰式から得られた値(予測値)と実際に測定された値(実測値)との差を表す。従って、誤差は計算で求められないが、残差は計算で求められる。誤差=実測値-真値、残差=実測値-予測値。
オッズとオッズ比を理解しよう
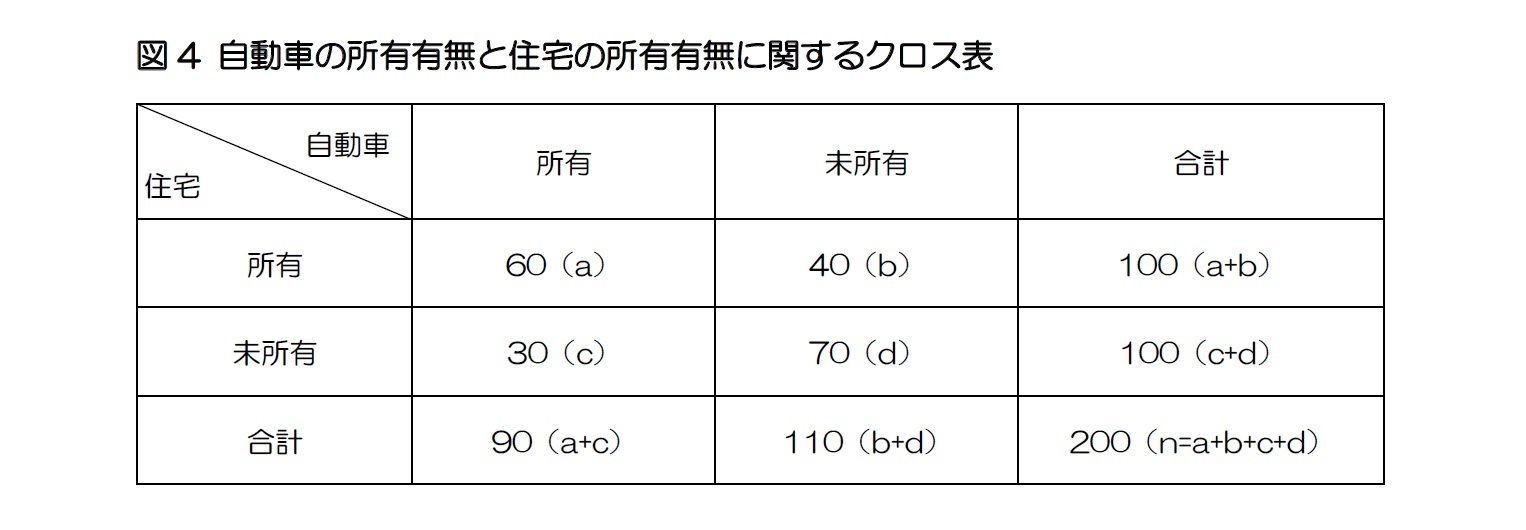
一方、オッズ比とは二つのオッズの比率であり、例えばオッズ比を利用すると、自動車を所有している世帯主が自動車を所有していない世帯主に比べて何倍住宅を所有しているかが計算できる。図表4は自動車の所有有無と住宅の所有有無を示しているクロス表であり、(1)自動車を所有している世帯主が住宅を所有しているオッズAと、(2)自動車を所有していない世帯主が住宅を所有しているオッズBを求めることが可能である。
但し、オッズ比が1より小さい(回帰係数が「-」)結果が出た場合は、求めた可能性が減少したことを意味するので解釈に注意が必要である。例えば、被説明変数として就業ダミー(就業を1、未就業を0)を用いて説明変数が「子供の数」が就業に与える影響を分析した結果、回帰係数が「-1.0416」が出て、オッズ比は「0.35289」が得られたと仮定しよう。この結果は子供の数が一人増えると、就業する可能性が0. 35289倍増加すると読み取ることができるものの、実際は子供の数が増えると就業する可能性が低くなることを意味する。しかしながら、初心者の場合は「0.35289」という正の数値を誤って解釈することも多いだろう。そこで、このような誤りを最大限防止するためにエクセルの数式((式6))を利用して値を変換することも一つの方法である。例えば、回帰係数「-1.0416」を(式6)に入れて計算すると「-64.7」という負の数値が得られる。つまり、この結果は子供の数が一人増えると、就業する可能性が64.7%減少することを意味するのであるが、負の数値であるため解釈による誤りを防ぐことができる。
ロジット変換
結びに代えて
4 統計分析の概要については、金 明中(2019)「統計分析を理解しよう-よく使われている統計分析方法の概要-」研究員の眼、2019年6月28日を参照すること。
参考文献
- 金 明中(2018)「回帰分析を理解しよう!-回帰分析の由来と概念、そして分析結果の評価について-」研究員の眼 2018年5月16日
- 金 明中(2019)「統計分析を理解しよう-よく使われている統計分析方法の概要-」研究員の眼、2019年6月28日
- 蓑谷 千凰彦(1997)『計量経済学』多賀出版
- 山澤 成康(2004)『実践計量経済学入門』日本評論社
- キム ギョンソク・キム ギョンヒ(2004)『Stataを用いた統計実務』統計庁STATA研究会
本資料記載のデータは各種の情報源から入手・加工したものであり、その正確性と完全性を保証するものではありません。
また、本資料は情報提供が目的であり、記載の意見や予測は、いかなる契約の締結や解約を勧誘するものではありません。
(2019年07月19日「ニッセイ年金ストラテジー」)
このレポートの関連カテゴリ

生活研究部 上席研究員・ヘルスケアリサーチセンター・ジェロントロジー推進室兼任
金 明中 (きむ みょんじゅん)
研究・専門分野
高齢者雇用、不安定労働、働き方改革、貧困・格差、日韓社会政策比較、日韓経済比較、人的資源管理、基礎統計
03-3512-1825
- プロフィール
【職歴】
独立行政法人労働政策研究・研修機構アシスタント・フェロー、日本経済研究センター研究員を経て、2008年9月ニッセイ基礎研究所へ、2023年7月から現職
・2011年~ 日本女子大学非常勤講師
・2015年~ 日本女子大学現代女性キャリア研究所特任研究員
・2021年~ 横浜市立大学非常勤講師
・2021年~ 専修大学非常勤講師
・2021年~ 日本大学非常勤講師
・2022年~ 亜細亜大学都市創造学部特任准教授
・2022年~ 慶應義塾大学非常勤講師
・2019年 労働政策研究会議準備委員会準備委員
東アジア経済経営学会理事
・2021年 第36回韓日経済経営国際学術大会準備委員会準備委員
【加入団体等】
・日本経済学会
・日本労務学会
・社会政策学会
・日本労使関係研究協会
・東アジア経済経営学会
・現代韓国朝鮮学会
・博士(慶應義塾大学、商学)
金 明中のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/07/08 | 「静かな退職」と「カタツムリ女子」の台頭-ハッスルカルチャーからの脱却と新しい働き方のかたち | 金 明中 | 基礎研マンスリー |
| 2025/06/06 | “サヨナラ”もプロに任せる時代-急増する退職代行サービス利用の背景とは? | 金 明中 | 基礎研マンスリー |
| 2025/06/02 | 日韓カップルの増加は少子化に歯止めをかけるか? | 金 明中 | 研究員の眼 |
| 2025/05/22 | 【アジア・新興国】韓国の生命保険市場の現状-2023年のデータを中心に- | 金 明中 | 保険・年金フォーカス |
新着記事
-
2025年10月14日
今週のレポート・コラムまとめ【10/7-10/10発行分】 -
2025年10月10日
企業物価指数2025年9月~国内企業物価の上昇率は前年比2.7%、先行きは鈍化予想~ -
2025年10月10日
中期経済見通し(2025~2035年度) -
2025年10月10日
保険・年金関係の税制改正要望(2026)の動き-関係する業界・省庁の改正要望事項など -
2025年10月10日
若者消費の現在地(4)推し活が映し出す、複層的な消費の姿~データで読み解く20代の消費行動
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【統計分析を理解しよう-ロジスティック回帰分析の概要-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
統計分析を理解しよう-ロジスティック回帰分析の概要-のレポート Topへ
























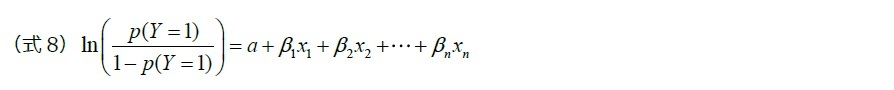
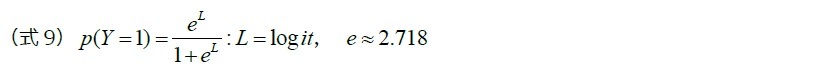
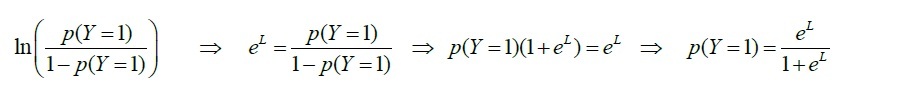


 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




