年末ジャンボ　くじ購入の配分法－２つの宝くじからどのようにポートフォリオを組成する?

保険研究部主席研究員兼気候変動リサーチセンターチーフ気候変動アナリスト兼ヘルスケアリサーチセンター主席研究員篠原拓也

このレポートの関連カテゴリ

今年も、11月から恒例の年末ジャンボ宝くじの発売が始まっている。前回のコラム(「年末ジャンボ今年はどう狙う－3つの高額当せんを踏まえて、くじの買い方を考えてみよう」篠原拓也(研究員の眼, ニッセイ基礎研究所, 2024年11月19日))のなかで、くじの内容や、それを踏まえた買い方について検討した。

そのなかで、「今年は、年末ジャンボを◇◇枚、年末ジャンボミニを△△枚買い揃えて、いろいろな高額当せんを狙ってみよう」という買い方について、2つの宝くじからポートフォリオを組成して、その価値を存分に味わう買い方だとしていた。だが、具体的なポートフォリオの組成については、特に言及していなかった。

そこで、本稿では、2つの宝くじからどのようにポートフォリオを組成するか? ― つまり、くじ購入の配分法、について検討してみたい。

◇ 現代ポートフォリオ理論をベースに検討する

まず、そもそも「2つの宝くじからなるポートフォリオ」という言い回しは、あまり聞きなれないかもしれない。ただ、“ポートフォリオ”などと大上段に構えなくても、生活の場面では、2種類のものを組み合わせて買う機会はしばしばある。

例えば、スーパーの惣菜コーナーに餃子のパックが並んでいるのをみて、それを今晩の夕食とすることにしたとしよう。餃子のパックには、焼餃子と、水餃子がある。どちらも食べたいので、それぞれ何パックか、ショッピングかごに入れることにした。さて、それぞれ何パックずつ買うべきか?　この場合、購入者はあまり意識せずに、焼餃子と水餃子のポートフォリオを組成しているといえる。

“ポートフォリオ”という用語は、証券投資でよく用いられる。一般に、証券投資の場面では、複数の証券について、各証券への投資金額を決定する。投資金額の総額が決まっている場合は、それをどの証券にどれだけの割合で投資するかという、配分を決めることとなる。

そこで、よく使われるのが「現代ポートフォリオ理論」だ。この理論の基盤となる分散投資理論を提唱したアメリカの経済学者ハリー・マーコウィッツ氏は、その功績により、1990年にノーベル経済学賞を受賞している。

本稿では、この理論をもとに、年末ジャンボと、年末ジャンボミニの2つの宝くじからなるポートフォリオを考えていくこととする。なお、もとになる宝くじは2つだが、その配分割合は無数に設定できるため、ポートフォリオの数も無数に考えられる。

◇ リターンは1等当せん金額、リスクは1等当せん金の標準偏差とする

現代ポートフォリオ理論は、ポートフォリオのリスクとリターンの関係を明らかにするものだ。その際、通常は、縦軸にリターンとしてポートフォリオの期待収益率、横軸にリスクとして収益率の標準偏差をとった座標平面が用いられる。

だが、宝くじの場合、平均的には買うと損をするものであり、期待収益率はマイナス50%程度となる。これをそのまま理論に当てはめても、結果の解釈は困難と考えられる。そこで、リスクとリターンの考え方について何か工夫をする必要がある。

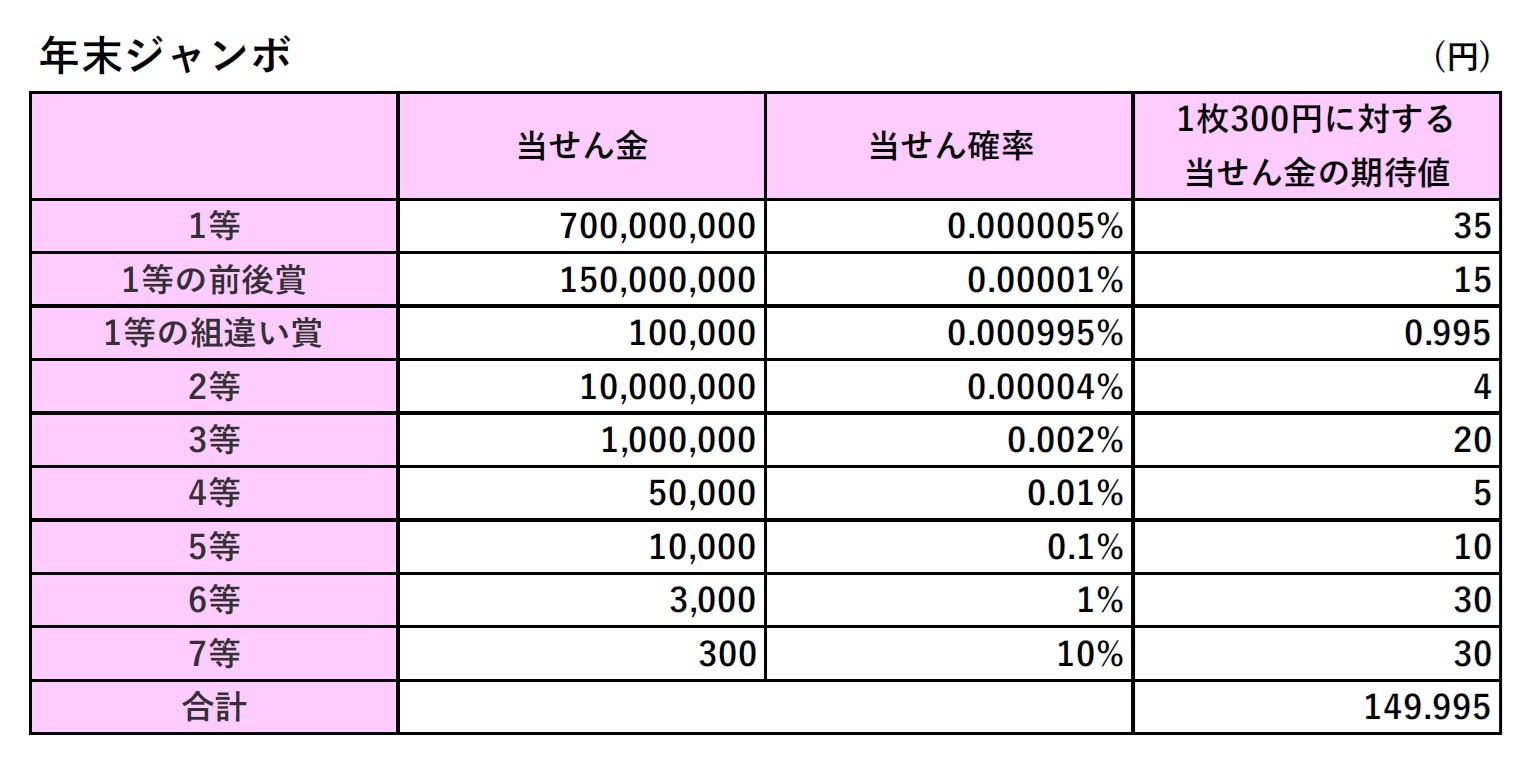
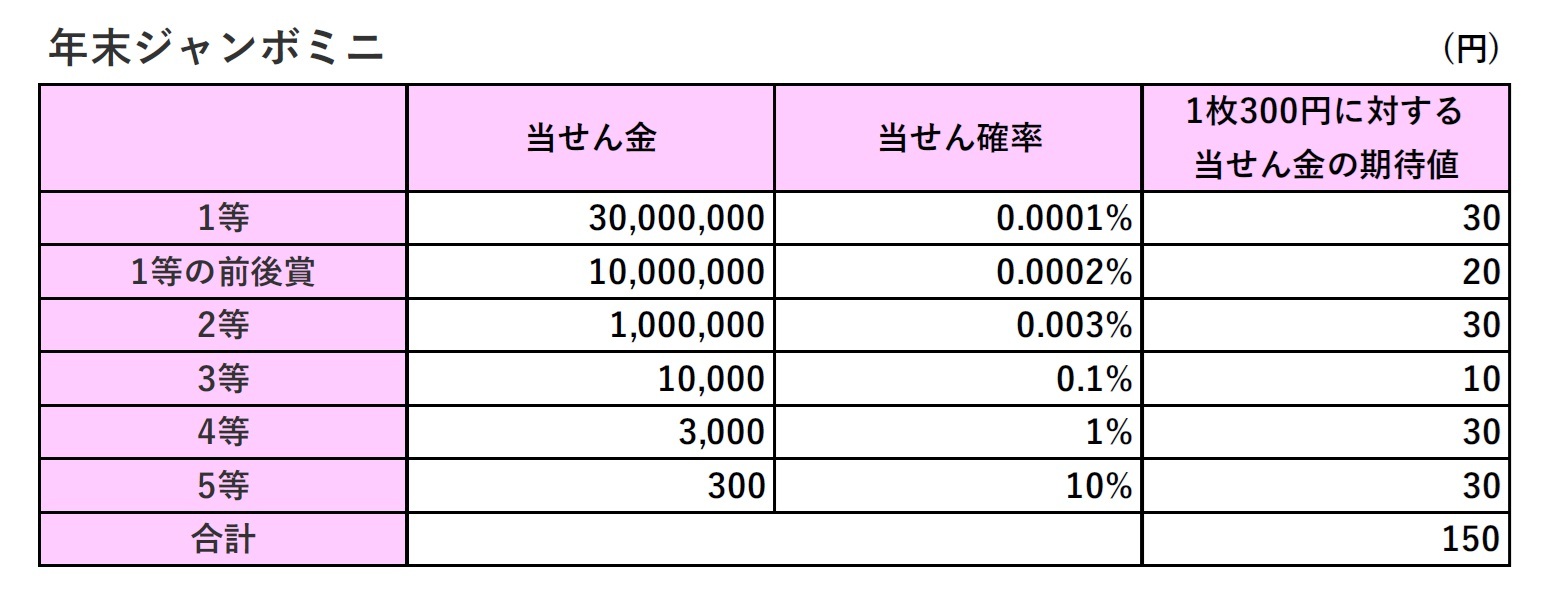
まず、リターンについて。宝くじのリターンとは何か? 一言でいえば、1等と前後賞の合計の当せん金額と言ってよいだろう。そこで、年末ジャンボは10億円、年末ジャンボミニは5000万円とする。

つぎに、リスクについて。これは、リターンに対応して、1等と前後賞の標準偏差、つまり、1等と前後賞の当せん金を受け取る場合のブレをリスクとみなすことにする。

具体的には、くじ1枚に対して、1等の賞金を前後賞の分も合わせて、年末ジャンボは10億円、年末ジャンボミニは5000万円とみなし、2等以下(1等の組違い賞を含む)の当せん金はすべてゼロとしたうえで、その標準偏差を計算してこれをリスクとする。(実際には、くじを連番で3枚買う場合、1等の前後賞だけが当せんするといったことも起こりうるが、今回は、話を簡単にするために、そうした一部分だけの当せんは考慮しない。)

このように、リターンとリスクを設定したうえで、話を進めていく。

◇ リスクを最小にするには年末ジャンボと年末ジャンボミニの配分割合をどうすべき?

こうして、リターンとリスクを設定したうえで、それらをグラフに表していく。

この図だが、横軸にリスク、縦軸にリターンをとっている。右に行くほどリスクが増大し、上に行くほどリターンが増えることになる。

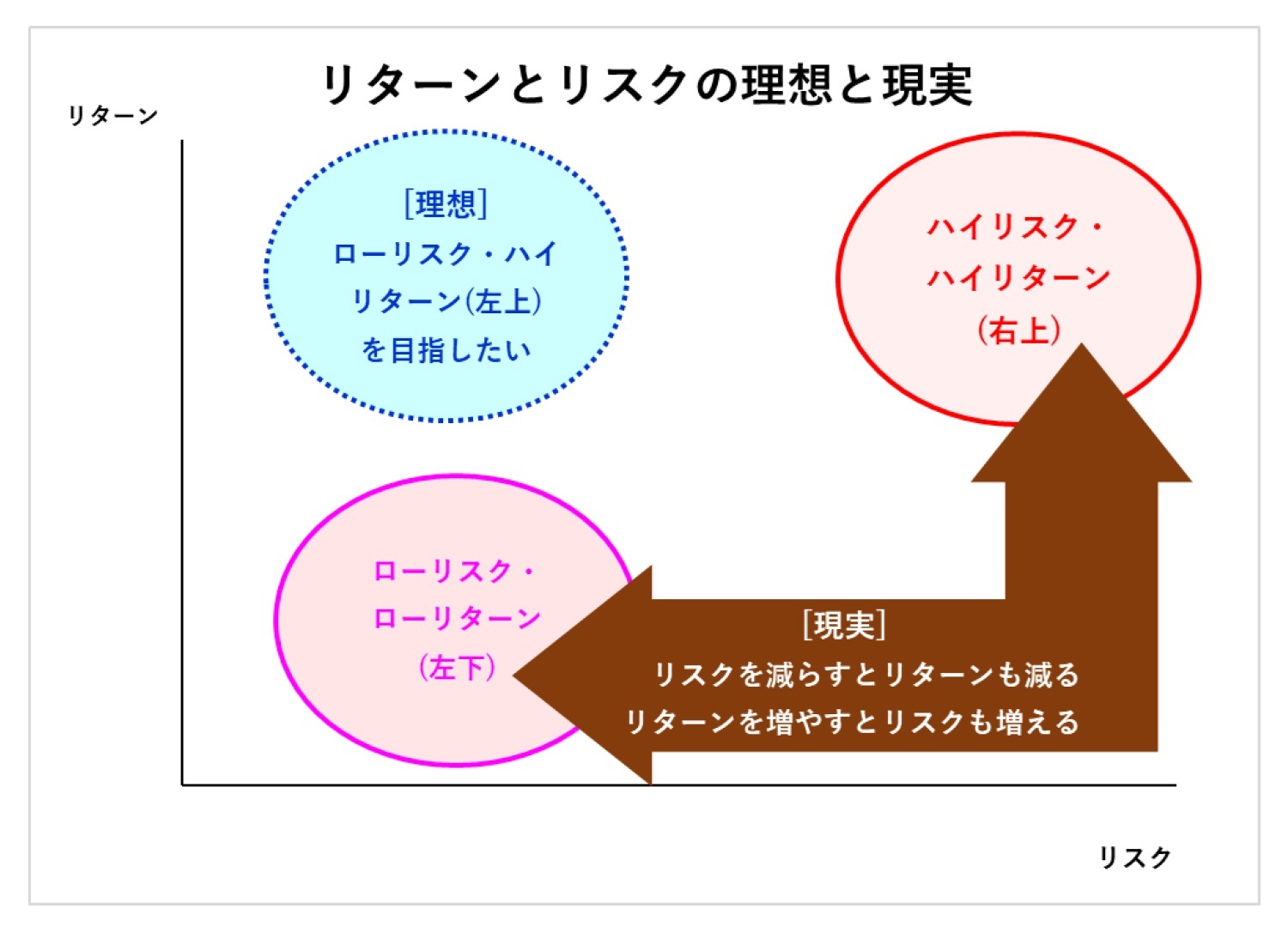
普通、たいていの人は「リスクはできるだけ小さく抑えつつ、リターンはできるだけ大きくしたい(ローリスク・ハイリターン)」と考えるだろう。この図でいうと、左上のほうを目指すことになる。

だが、現実はそう甘くはない。リスクを小さくしたければリターンも小さくなってしまう。リスクを大きくとらないと、大きなリターンは得られない。まさに、「虎穴(こけつ)に入らずんば虎児(こじ)を得ず」ということわざそのものだ。

図で言えば、ローリスク・ローリターンならば左下、ハイリスク・ハイリターンならば右上のほうに行く。左上のほうには、なかなか行くことができない。

そこで、2つの宝くじをある比率で購入するポートフォリオで、リスクとリターンの関係がどうなるかを図に表してみて、その中からできるだけ左上のほうのポートフォリオを選ぶ ―― これが、現代ポートフォリオ理論の考え方をもとにした、今回の宝くじ購入の配分法の核心部分だ。

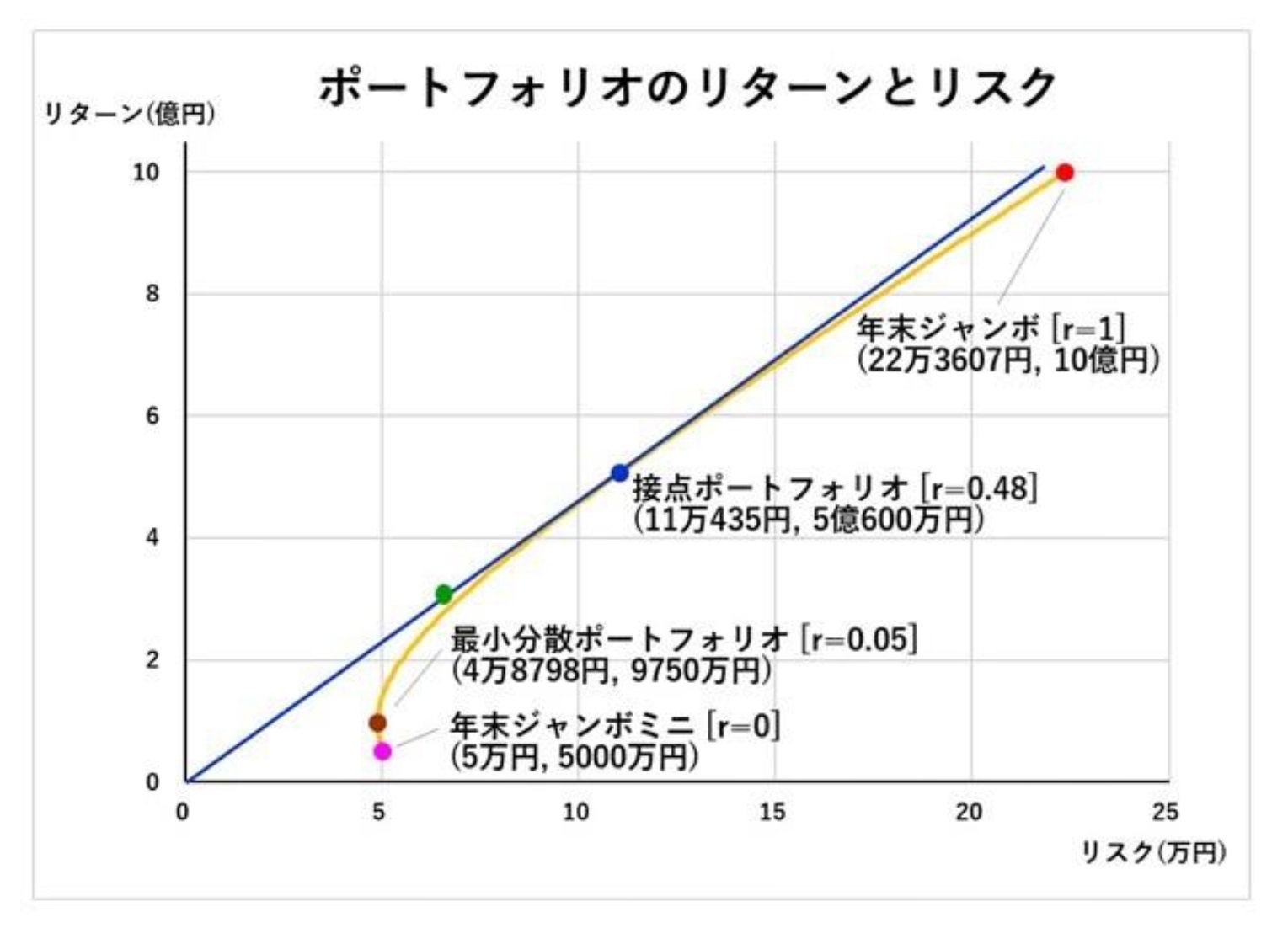
次の図では、まず、右上の端点に年末ジャンボ、左下の端点に年末ジャンボミニがくる。そして、2つの宝くじへの配分割合(年末ジャンボにr、年末ジャンボミニに(1-r) (0≦r≦1) 配分)をいろいろ変えていった場合のポートフォリオの点がその間に並ぶ。それらを表したものが、オレンジ色の曲線のグラフだ。なお、2つの宝くじは独立に行われるとして、相関関係はないもの(相関係数はゼロ)と想定している。

年末ジャンボだけを購入した場合が赤い点、年末ジャンボミニだけを購入した場合がピンク色の点に相当する。

年末ジャンボのリスクは22万3607円、リターンは10億円。一方、年末ジャンボミニのリスクは5万円、リターンは5000万円だ。これらの金額は、図の中では、(22万3607円, 10億円)とか、(5万円, 5000万円)といった感じで、中学校の数学で習う座標平面の(x座標, y座標)のように表示している。

茶色の点は、r＝0.05の場合で、リスクを最小にしたもの、つまり1等と前後賞の当せん金の受取額のブレを最小にしたものだ。投資理論では、「最小分散ポートフォリオ」と呼ばれる。

これは、あるお金を全てつかって2つの宝くじを買う場合に、とにかくリスクをできるだけ減らしたいという場合の買い方だ。「最小分散」のときには標準偏差が最小となり、リスクが最も小さくなる。

つまり、リスクを最小にしたいのならば、年末ジャンボと年末ジャンボミニの配分割合を5%と95%の割合で買えばよいという結果になる。

この場合、リターン、つまり1等前後賞合わせての当せん金は9750万円となる。リスクの大きい年末ジャンボには5%しかお金を投入しないため、1等前後賞のリターンは9750万円にとどまることとなる。まさに、ローリスク・ローリターンとなっている。ただし、冷静に見れば、9750万円のリターンでも十分に大きな金額という気がしてくる。

日付	タイトル	執筆者	媒体
2025/04/01	1, 2, 4, 8, 16, ○, …－思い込みには要注意！	篠原拓也	研究員の眼
2025/03/25	産業クラスターを通じた脱炭素化－クラスターは温室効果ガス排出削減の潜在力を有している	篠原拓也	基礎研レター
2025/03/18	気候変動:アクチュアリースキルの活用－「プラネタリー・ソルベンシー」の枠組みに根差したリスク管理とは?	篠原拓也	基礎研レター
2025/03/11	国民負担率 24年度45.8%の見込み－高齢化を背景に、欧州諸国との差は徐々に縮小	篠原拓也	研究員の眼

日付

タイトル

執筆者

媒体

2025/04/01

1, 2, 4, 8, 16, ○, …－思い込みには要注意！

篠原拓也

研究員の眼

2025/03/25

産業クラスターを通じた脱炭素化－クラスターは温室効果ガス排出削減の潜在力を有している

篠原拓也

基礎研レター