- シンクタンクならニッセイ基礎研究所 >
- 暮らし >
- 消費者行動 >
- 対数(自然対数)を理解しよう!-対数の定義と分析結果の解釈について-
文字サイズ
- 小
- 中
- 大
1――はじめに
2――対数の定義
対数は英語でlogarithmと書き、記号logを用いて表され、10を底とする常用対数(log、以下、対数)とeを底とする自然対数(ln)に分けられる。
一般的に対数は、「aを何乗すれば、すなわち何回かければbになるか」を考えるときに使われ、式としてはlogab=xのように書く。例えば5を何乗すれば125になるかを計算するときには、5を底として125を真数3とする対数を求めると「3」(5を3乗すると125になるという意味)という答えが得られる。
エクセルを使う場合には、LOG関数を使うと、次のように簡単に対数を求めることができる。
ax=b(a≠1,a>0,b>0)という条件を満たしている場合
(x)は(a)を底とする(b)の対数といい、次のように表すことができる。
x=logab (aを何(x)乗したらbになるのか?)
1 松村 明編集(2006)『大辞林 第三版』三省堂
2 山田 忠雄・柴田 武・酒井 憲二・倉持 保男・山田 明雄・上野 善道・井島 正博・笹原 宏之編集(2011)『新明解国語辞典 第七版』三省堂
3 対数y=logaxにおいて、xは対数yの真数である。逆対数ともいう。英語ではantilogarithm。
3――自然対数の定義と分析結果の解析
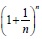 でnをだんだん大きくしていくと到達する数字であり、その値は2.71828…という、いつまでも続く、循環しない無限小数である。これを式で表すと次の通りである。
でnをだんだん大きくしていくと到達する数字であり、その値は2.71828…という、いつまでも続く、循環しない無限小数である。これを式で表すと次の通りである。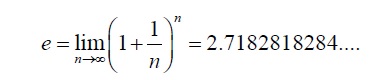
一つ、面白いことは底eが省略可能な点であり、回帰分析などでは、log5やlogx、あるいはln5やlnxという書き方で使われている。
では、自然対数が回帰分析などの実証分析に使われたとき、その結果をどのように解析すればいいだろうか。一般的には次のような四つのケースが考えられる4。
(1) 被説明変数と説明変数両方とも対数変換をしていないケース
y=β0+β1x+uで他の要因が固定されている場合に、xの1単位の増加はyのβ1単位の増加をもたらす。例えば、勉強時間(x)が成績(y)に与えた影響をみるために回帰分析を行い、y=β0+2.5β1x+uという結果が得られた場合、勉強時間を1時間増やした場合に、2.5点の成績が上がると解析することができる。
(2) 被説明変数は対数変換をせず、説明変数だけ対数変換をしたケース
y=β0+β1logx+uで、他の要因が固定されている場合に、logxの0.1単位の増加はyの0.1β1単位の増加をもたらす。一般的に増加率が小さいときにはlogxの0.1単位の増加は近似的にxが10%増加したと推測することができるので、他の要因が固定されている場合にxが10%増加することはyが0.1β1単位増加したと見ることが可能である。
(3) 被説明変数は対数変換をして、説明変数は対数変換をしていないケース
logy=β0+β1x+uでβ1の値が小さく、他の要因が固定されている場合に、xの1単位の増加はlogyをβ1増加させる。つまり、yは100×β1%増加することになる(β1の値が小さい必要がある)。
例えば、賃金がyで学歴がx(単位は年)であり、logy=β0+0.07x+uという分析結果が得られたとしよう。分析の結果は、他の要因が固定されている場合に学歴が1年分高くなるにつれてlog賃金は0.07高くなると解析することができる。さらに上記の基準を適用すると学歴が1年分高くなるにつれて賃金は7%高くなると言うことが可能である。
(4) 被説明変数と説明変数両方とも対数変換をしたケース
logy=β0+β1logx+uで、他の要因が固定されている場合にはlogxが0.01増加すると、logyは0,01β1増加すると解析することができる。つまり、他の要因が固定されている場合にxの1%の増加はyの約β1%の増加をもたらすと推測される。
では、この条件を利用して、需要の価格弾力性を求めてみよう。例えば、ある財の価格がy、需要量(単位はkg)がxであり、logy=β0-0.71logx+uという分析結果が得られた場合、この結果は価格が1%上昇すると、需要量は約0.7%減少すると考えることができる。
4 ハンチロック(2017)『計量経済学講義第2版』(株)博英社を一部引用・加筆した。
4――結びに代えて
(2018年01月17日「基礎研レター」)
このレポートの関連カテゴリ

生活研究部 上席研究員・ヘルスケアリサーチセンター・ジェロントロジー推進室兼任
金 明中 (きむ みょんじゅん)
研究・専門分野
高齢者雇用、不安定労働、働き方改革、貧困・格差、日韓社会政策比較、日韓経済比較、人的資源管理、基礎統計
03-3512-1825
- プロフィール
【職歴】
独立行政法人労働政策研究・研修機構アシスタント・フェロー、日本経済研究センター研究員を経て、2008年9月ニッセイ基礎研究所へ、2023年7月から現職
・2011年~ 日本女子大学非常勤講師
・2015年~ 日本女子大学現代女性キャリア研究所特任研究員
・2021年~ 横浜市立大学非常勤講師
・2021年~ 専修大学非常勤講師
・2021年~ 日本大学非常勤講師
・2022年~ 亜細亜大学都市創造学部特任准教授
・2022年~ 慶應義塾大学非常勤講師
・2019年 労働政策研究会議準備委員会準備委員
東アジア経済経営学会理事
・2021年 第36回韓日経済経営国際学術大会準備委員会準備委員
【加入団体等】
・日本経済学会
・日本労務学会
・社会政策学会
・日本労使関係研究協会
・東アジア経済経営学会
・現代韓国朝鮮学会
・博士(慶應義塾大学、商学)
金 明中のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/07/08 | 「静かな退職」と「カタツムリ女子」の台頭-ハッスルカルチャーからの脱却と新しい働き方のかたち | 金 明中 | 基礎研マンスリー |
| 2025/06/06 | “サヨナラ”もプロに任せる時代-急増する退職代行サービス利用の背景とは? | 金 明中 | 基礎研マンスリー |
| 2025/06/02 | 日韓カップルの増加は少子化に歯止めをかけるか? | 金 明中 | 研究員の眼 |
| 2025/05/22 | 【アジア・新興国】韓国の生命保険市場の現状-2023年のデータを中心に- | 金 明中 | 保険・年金フォーカス |
新着記事
-
2025年11月04日
今週のレポート・コラムまとめ【10/28-10/31発行分】 -
2025年10月31日
交流を広げるだけでは届かない-関係人口・二地域居住に求められる「心の安全・安心」と今後の道筋 -
2025年10月31日
ECB政策理事会-3会合連続となる全会一致の据え置き決定 -
2025年10月31日
2025年7-9月期の実質GDP~前期比▲0.7%(年率▲2.7%)を予測~ -
2025年10月31日
保険型投資商品の特徴を理解すること(欧州)-欧州保険協会の解説文書
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【対数(自然対数)を理解しよう!-対数の定義と分析結果の解釈について-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
対数(自然対数)を理解しよう!-対数の定義と分析結果の解釈について-のレポート Topへ


















 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




