- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 複素数について(その1)-虚数・複素数とは(その歴史と概要)-
NEW
コラム
2025年05月15日
文字サイズ
- 小
- 中
- 大
はじめに
これまでの研究員の眼において、数字に関して、「0」を始めとした各種の数字、負の数、小数、分数、さらには無理数等について、シリーズで報告してきた。これらの報告を通じて、ほぼ実数の世界における数字について、主なテーマをカバーしてきた(もちろん、「代数的数」や「超越数」といったようなさらなるテーマもあるが、これらについては別途の機会に譲ることとしている)。
さて、皆さんは、「虚数」あるいは虚数と実数で構成される「複素数」と呼ばれる数字はご存知だと思う。
「虚数」といえば、多くの方々は、高校時代に「二乗するとマイナス1」になる数としての「i」について学んだことを思い出されるだろう。二次方程式の解等で出てくることでそれなりに認識しておられる方も多いと思われる。大学の入試問題等でも、「虚数」や「複素数」に関する問題もいくつか出題されることから、「虚数」なるものがどのようなものであるかについては、それなりに勉強していたのではないかと思われる。
ところが、それでは、なぜそれが重要なのか等については、殆ど興味・関心を持つこともなかったか、あるいはその余裕もなかったというのが実状であると思われる。さらには、一部の人を除けば、大学受験以来「虚数」なるものにはとんとお世話になったことはなく、「虚数」(あるいは「複素数」)なんて、何の役にも立っていないものだ、と思われている方も多いのではないかと思われる。実は、「虚数」(あるいは「複素数」)は極めて重要な概念で、現代社会において必要不可欠なものになっている。
今回は、「虚数」及び虚数と実数で構成される「複素数」について、今一度それがどのようなもので、どんな性質を有しており、はたまたそれがどのように社会で役立っているのか等について、何回かに分けて報告していきたいと思う。
まずは、今回は、「虚数」とは何か、から初めて、虚数と複素数の歴史と概要について、説明していきたい。
さて、皆さんは、「虚数」あるいは虚数と実数で構成される「複素数」と呼ばれる数字はご存知だと思う。
「虚数」といえば、多くの方々は、高校時代に「二乗するとマイナス1」になる数としての「i」について学んだことを思い出されるだろう。二次方程式の解等で出てくることでそれなりに認識しておられる方も多いと思われる。大学の入試問題等でも、「虚数」や「複素数」に関する問題もいくつか出題されることから、「虚数」なるものがどのようなものであるかについては、それなりに勉強していたのではないかと思われる。
ところが、それでは、なぜそれが重要なのか等については、殆ど興味・関心を持つこともなかったか、あるいはその余裕もなかったというのが実状であると思われる。さらには、一部の人を除けば、大学受験以来「虚数」なるものにはとんとお世話になったことはなく、「虚数」(あるいは「複素数」)なんて、何の役にも立っていないものだ、と思われている方も多いのではないかと思われる。実は、「虚数」(あるいは「複素数」)は極めて重要な概念で、現代社会において必要不可欠なものになっている。
今回は、「虚数」及び虚数と実数で構成される「複素数」について、今一度それがどのようなもので、どんな性質を有しており、はたまたそれがどのように社会で役立っているのか等について、何回かに分けて報告していきたいと思う。
まずは、今回は、「虚数」とは何か、から初めて、虚数と複素数の歴史と概要について、説明していきたい。
虚数とは、複素数とは
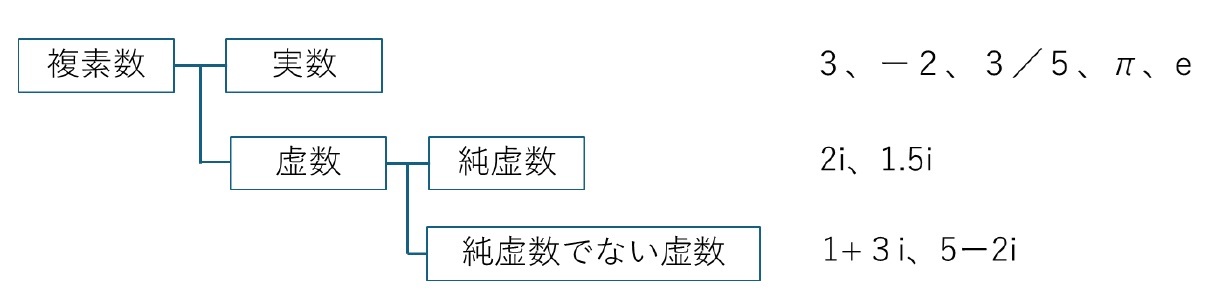
実数のaとbは、それぞれ複素数の「実部」(又は「実数部」)と「虚部」(又は「虚数部」)と呼ばれる。複素数z=a+bi の実部と虚部はそれぞれ、Re zやIm z等で表される。
また、複素数z=a+bi に対して、複素数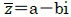 をzの「共役な複素数」又は「共役複素数」、英語では「complex conjugate」と呼ぶ。
をzの「共役な複素数」又は「共役複素数」、英語では「complex conjugate」と呼ぶ。
また、複素数z=a+bi に対して、複素数
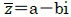 をzの「共役な複素数」又は「共役複素数」、英語では「complex conjugate」と呼ぶ。
をzの「共役な複素数」又は「共役複素数」、英語では「complex conjugate」と呼ぶ。
虚数や複素数の歴史
虚数を発見したのは、16世紀のイタリアの数学者で医者でもあったジェロラモ・カルダノ(Gerolamo Cardano)1だと言われている。カルダノは、1545年の著書『Ars Magna(アルス・マグナ)』2の中で、三次方程式の解の公式、四次方程式の解法3を示した。三次方程式の解の公式については、同じくイタリアの数学者のニコロ・フォンタナ(通称タルタリア)(Niccolò Fontana "Tartaglia")4との関係で有名ないわくつきのものであったが、ここではその内容については触れない。いずれにしても、カルダノは、三次方程式の解を示す際に世界で初めて虚数の概念を導入した。『Ars Magna(アルス・マグナ)』の中で「足して10、掛けて40になる二つの数はなにか」との問題に対する解(の候補)5として、以下の2つを挙げている。
また、同じくイタリアの数学者であるラファエル・ボンベリ(Rafael Bombelli)は、1572年の著書『L'Algebra(代数学)』で、三次方程式の解法を考案していたイタリアの数学者であるシピオーネ・デル・フェッロ(Scipione del Ferro)とタルタリアの方法を用いて方程式を解いて、(現在の)+i と −i に相当する概念に特別な名前を付与し、それらが代数学でどのような役割を果たすかを示した。ボンベリはその著書の中で、(現在の)複素数に関する性質や複素数に関する算術規則を説明している。これらにより、ボンベリは虚数研究の中心的な人物とみなされている。
しかし当時は、かつての0(ゼロ)と同じように、負の数ですらあまり理解されておらず、ましてや負の数の平方根である虚数については、架空のもの、役に立たないものとみなされている状況であった。17世紀の偉大な数学者かつ哲学者であるルネ・デカルト(René Descartes)ですら、虚数の概念を否定的にとらえており、1637年の著書『La Géométrie(幾何学)』では、これをフランス語で「nombre imaginaire(想像上の数)」と名付けている。これが英語の「imaginary number」となり、日本語の「虚数」の語源になっている。「実数」が現実に存在する数であるのに対して、「虚数」は現実には存在しない数、との意味合いが込められている6。
その後、1770年頃に、レオンハルト・オイラー(Leonhard Euler)によって、虚数単位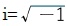 が導入された(これも、ラテン語の「imaginarius」の頭文字から採られている)。ただし、そのオイラーですら、負の数の平方根は数の仲間として認められるべきではない、との考え方を有していたようである。
が導入された(これも、ラテン語の「imaginarius」の頭文字から採られている)。ただし、そのオイラーですら、負の数の平方根は数の仲間として認められるべきではない、との考え方を有していたようである。
ヨハン・カール・フリードリヒ・ガウス(Johann Carl Friedrich Gauß)は、1796年に、正十七角形が定規とコンパスだけでは作図できないことを発見しているが、この時に複素数平面のアイデアを有していたとされている。ガウスは、その後1799年に、「代数学の基本定理7」の証明を行い8、その後に複素数平面を導入9している。さらにはオーギュスタン=ルイ・コーシー(Augustin Louis Cauchy)らによって、複素解析の研究も進められていった。これらの数学者の研究や貢献によって、虚数や複素数の概念が、徐々に多くの数学者や人々に受け入れられるようになっていった。
ガウスは、1831年に、複素数のことをドイツ語で「Komplexe Zahl」と名付けており、これが英語では「complex number」となった(これをそのまま翻訳すると「複合数」ということになる)。日本語の「複素数」は、日本において初めて日本人の生命表を作成したことでも有名な藤澤利喜太郎氏によって名付けられたとされている。複数の要素で構成される数、という意味合いから来ているものと思われる。
1 カルダノは賭博が好きで、1560年代に『Liber de ludo aleae(さいころあそびについて)』を執筆(発行は彼の死後の1663年)して、初めて系統的に確率論を論じたことでも知られている。
2 「偉大なる(技)術」や「大いなる技法」等と訳される。
3 一般的な四次方程式の解法は、カルダノの弟子であるルドヴィコ・フェラーリ(Ludovico Ferrari)によって発見された。
4 因みに、ガリレオ・ガリレイは、彼の孫弟子である。
5 カルダノは、解として認めていたわけではなく、形式的に解を求めれば、として2つを挙げていた。
6 漢字の「虚」は、虚しい、何もない、形だけで実質が伴わない、嘘・偽り等のネガティブな意味合いを有しているが、その名称に関わらず、現代において「虚数」及び「複素数」は必要不可欠で極めて重要な役割を果たすものとなっている。
7 「次数が 1 以上の任意の複素係数の一変数多項式には複素根が存在する」というものであるが、多項式P(x)の根は多項式方程式P(x)=0の解であることから「複素係数の一変数代数方程式は複素数の範囲で必ず解をもつ」と言うこともできる。
8 この時のガウスの証明は完全ではなかったが、後年に3つの異なる証明を与えている。
9 平面上の点としての複素数の幾何学的意義は、1797年にノルウェーの数学者であるカスパー・ウェッセル(Caspar Wessel )によって最初に記述された、とされている。
しかし当時は、かつての0(ゼロ)と同じように、負の数ですらあまり理解されておらず、ましてや負の数の平方根である虚数については、架空のもの、役に立たないものとみなされている状況であった。17世紀の偉大な数学者かつ哲学者であるルネ・デカルト(René Descartes)ですら、虚数の概念を否定的にとらえており、1637年の著書『La Géométrie(幾何学)』では、これをフランス語で「nombre imaginaire(想像上の数)」と名付けている。これが英語の「imaginary number」となり、日本語の「虚数」の語源になっている。「実数」が現実に存在する数であるのに対して、「虚数」は現実には存在しない数、との意味合いが込められている6。
その後、1770年頃に、レオンハルト・オイラー(Leonhard Euler)によって、虚数単位
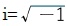 が導入された(これも、ラテン語の「imaginarius」の頭文字から採られている)。ただし、そのオイラーですら、負の数の平方根は数の仲間として認められるべきではない、との考え方を有していたようである。
が導入された(これも、ラテン語の「imaginarius」の頭文字から採られている)。ただし、そのオイラーですら、負の数の平方根は数の仲間として認められるべきではない、との考え方を有していたようである。ヨハン・カール・フリードリヒ・ガウス(Johann Carl Friedrich Gauß)は、1796年に、正十七角形が定規とコンパスだけでは作図できないことを発見しているが、この時に複素数平面のアイデアを有していたとされている。ガウスは、その後1799年に、「代数学の基本定理7」の証明を行い8、その後に複素数平面を導入9している。さらにはオーギュスタン=ルイ・コーシー(Augustin Louis Cauchy)らによって、複素解析の研究も進められていった。これらの数学者の研究や貢献によって、虚数や複素数の概念が、徐々に多くの数学者や人々に受け入れられるようになっていった。
ガウスは、1831年に、複素数のことをドイツ語で「Komplexe Zahl」と名付けており、これが英語では「complex number」となった(これをそのまま翻訳すると「複合数」ということになる)。日本語の「複素数」は、日本において初めて日本人の生命表を作成したことでも有名な藤澤利喜太郎氏によって名付けられたとされている。複数の要素で構成される数、という意味合いから来ているものと思われる。
1 カルダノは賭博が好きで、1560年代に『Liber de ludo aleae(さいころあそびについて)』を執筆(発行は彼の死後の1663年)して、初めて系統的に確率論を論じたことでも知られている。
2 「偉大なる(技)術」や「大いなる技法」等と訳される。
3 一般的な四次方程式の解法は、カルダノの弟子であるルドヴィコ・フェラーリ(Ludovico Ferrari)によって発見された。
4 因みに、ガリレオ・ガリレイは、彼の孫弟子である。
5 カルダノは、解として認めていたわけではなく、形式的に解を求めれば、として2つを挙げていた。
6 漢字の「虚」は、虚しい、何もない、形だけで実質が伴わない、嘘・偽り等のネガティブな意味合いを有しているが、その名称に関わらず、現代において「虚数」及び「複素数」は必要不可欠で極めて重要な役割を果たすものとなっている。
7 「次数が 1 以上の任意の複素係数の一変数多項式には複素根が存在する」というものであるが、多項式P(x)の根は多項式方程式P(x)=0の解であることから「複素係数の一変数代数方程式は複素数の範囲で必ず解をもつ」と言うこともできる。
8 この時のガウスの証明は完全ではなかったが、後年に3つの異なる証明を与えている。
9 平面上の点としての複素数の幾何学的意義は、1797年にノルウェーの数学者であるカスパー・ウェッセル(Caspar Wessel )によって最初に記述された、とされている。
複素数平面
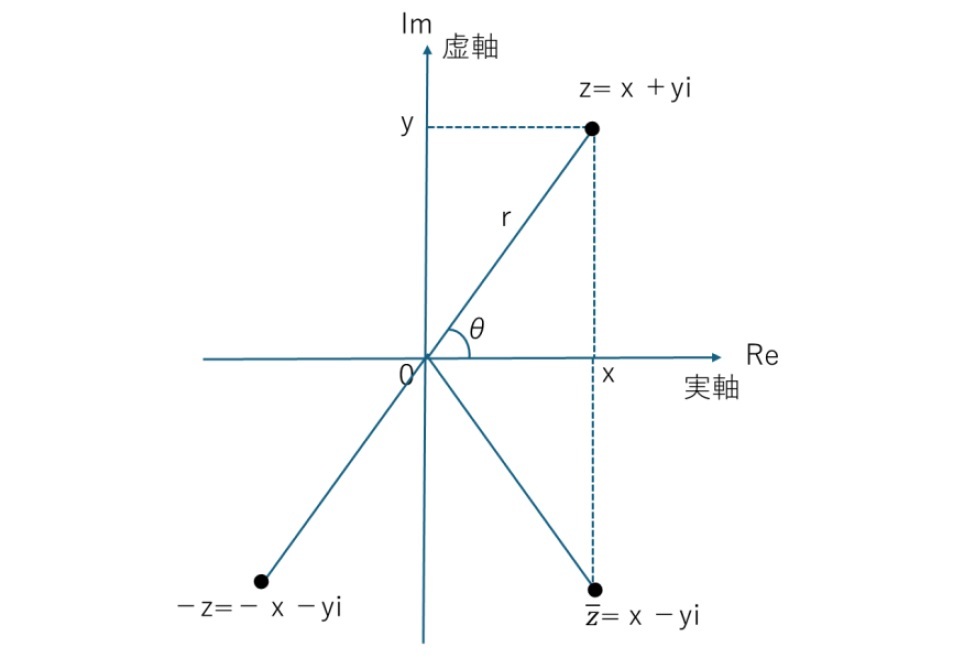
複素数を幾何学的に表現するものとして、「複素数平面(complex plane)」がある。これは、複素数z=x+yi を直交座標(x,y)に対応させた直交座標平面を指している。x軸が複素数の実部を表し「実軸(real axis)」(又は「実数軸」)、y軸が複素数の虚部を表し「虚軸(imaginary axis)」(又は「虚数軸」)と呼ばれる。
これは、先に述べたように1811年頃にガウスによって導入されたため「ガウス平面(Gaussian plane)」とも呼ばれる。また、そもそも「複素数平面」ではなく、「複素平面」とも呼ばれる10。さらには、1806年にスイス・ジュネーブのアマチュア数学者であるジャン・ロベール・アルガン(Jean-Robert Argand)11が「アルガン図(Argan Diagram)」と呼ばれる同様のアイデアを発表していることから、「アルガン平面」とも呼ばれる。
この複素数平面によれば、実数は実軸上、虚数は複素数平面から実軸を除いた部分、純虚数は虚軸上の点で表されることになる。この時、複素数zと複素数−𝑧は原点に対して対称となり、複素数𝑧とその共役複素数は実軸に対して対称となる。
なお、複素数z=x+yi に対応する複素数平面上の点をZとした場合、ベクトル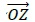 を考えることで、複素数を複素数平面上のベクトルに対応させて考えることができる。
を考えることで、複素数を複素数平面上のベクトルに対応させて考えることができる。
これは、先に述べたように1811年頃にガウスによって導入されたため「ガウス平面(Gaussian plane)」とも呼ばれる。また、そもそも「複素数平面」ではなく、「複素平面」とも呼ばれる10。さらには、1806年にスイス・ジュネーブのアマチュア数学者であるジャン・ロベール・アルガン(Jean-Robert Argand)11が「アルガン図(Argan Diagram)」と呼ばれる同様のアイデアを発表していることから、「アルガン平面」とも呼ばれる。
この複素数平面によれば、実数は実軸上、虚数は複素数平面から実軸を除いた部分、純虚数は虚軸上の点で表されることになる。この時、複素数zと複素数−𝑧は原点に対して対称となり、複素数𝑧とその共役複素数は実軸に対して対称となる。
なお、複素数z=x+yi に対応する複素数平面上の点をZとした場合、ベクトル
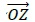 を考えることで、複素数を複素数平面上のベクトルに対応させて考えることができる。
を考えることで、複素数を複素数平面上のベクトルに対応させて考えることができる。
10 高校の学習指導要領では「複素数平面」となっているが、大学以上の教科書では「複素平面」や「ガウス平面」という用語が多用されているようである。
11 アルガンは、1814年の著作で、代数学の基本定理の最初の厳密な証明を与えたことでも知られている。
複素数の極形式
複素数を実部と虚部で表すのとは別の方法として、複素数平面上の点 P を、(1)原点 Oからの距離(複素数の「絶対値」(あるいは「大きさ」とも言われる))と、(2)正の実軸と線分 OP の見込む角を反時計回りに測ったもの(複素数の「偏角」)、の対で表す方法があり、これを「複素数の極形式(polar form)」、あるいは、「直交座標表示」に対して、「極座標表示」と呼んでいる。
具体的には、先の図において、複素数z = x + yi(x, y は実数)において、直交座標系(x, y)に対応する極座標系を (r, θ)(r 0)とするとき、
z=r(cos θ+i sin θ)
と表すことができる。ここで、rはzの絶対値、θはzの偏角で、以下の通りである。
具体的には、先の図において、複素数z = x + yi(x, y は実数)において、直交座標系(x, y)に対応する極座標系を (r, θ)(r 0)とするとき、
z=r(cos θ+i sin θ)
と表すことができる。ここで、rはzの絶対値、θはzの偏角で、以下の通りである。
有名な「オイラーの公式(eiθ =cos θ+i sin θ)」を用いると、これは
z=r eiθ
となる(これを「指数関数表示」と呼んだりする)。
z=r eiθ
となる(これを「指数関数表示」と呼んだりする)。
(2025年05月15日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/05/15 | 複素数について(その1)-虚数・複素数とは(その歴史と概要)- | 中村 亮一 | 研究員の眼 |
| 2025/05/02 | 曲線にはどんな種類があって、どう社会に役立っているのか(その11)-螺旋と渦巻の実例- | 中村 亮一 | 研究員の眼 |
| 2025/04/25 | 欧州大手保険グループの2024年の生命保険新契約業績-商品タイプ別・地域別の販売動向・収益性の状況- | 中村 亮一 | 基礎研レポート |
| 2025/04/14 | 欧州大手保険グループの地域別の事業展開状況-2024年決算数値等に基づく現状分析- | 中村 亮一 | 基礎研レポート |
新着記事
-
2025年05月15日
複素数について(その1)-虚数・複素数とは(その歴史と概要)- -
2025年05月15日
いま振り返るベヴァリッジ報告-少子化対策も組み込んだ80年前の社会保障計画- -
2025年05月15日
若手人材の心を動かす、企業の「社会貢献活動」とは(3)-「行動科学」で考える、パーパスと従業員の自発行動のつなぎ方 -
2025年05月14日
インド消費者物価(25年4月)~4月のCPI上昇率は+3.2%、食品インフレの減速続く -
2025年05月14日
企業物価指数2025年4月~国内企業物価は5ヵ月連続で前年比4%台~
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年04月02日
News Release
-
2024年11月27日
News Release
-
2024年07月01日
News Release
【複素数について(その1)-虚数・複素数とは(その歴史と概要)-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
複素数について(その1)-虚数・複素数とは(その歴史と概要)-のレポート Topへ



















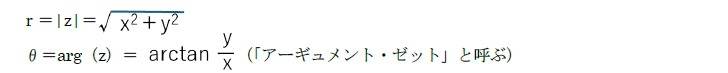

 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




