- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 複素数について(その2)-複素数と方程式-
コラム
2025年05月28日
文字サイズ
- 小
- 中
- 大
(参考)カルダノの公式
さて、三次方程式の解法はいくつかあり、解の公式も知られている。あまり簡明な式とはいえないが、ここでは「カルダノの公式」と呼ばれているものを簡単に紹介しておく。
三次方程式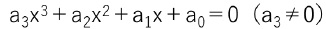 について考える。
について考える。
三次方程式
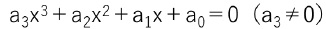 について考える。
について考える。
となる。よって、最初の方程式の解は、このyからA2/3 を差し引いたものとなる。
ところで、このカルダノの公式によれば、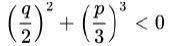 の時に負の数の平方根が現れる形になる。一方で、これは先に述べた三次方程式の判別式D>0の場合に相当していることから、相異なる3個の実数解を持つ条件に合致していることになる。即ち、実数解しかないにもかかわらず、カルダノの公式では「負の数の平方根」が現れてくることになる。
の時に負の数の平方根が現れる形になる。一方で、これは先に述べた三次方程式の判別式D>0の場合に相当していることから、相異なる3個の実数解を持つ条件に合致していることになる。即ち、実数解しかないにもかかわらず、カルダノの公式では「負の数の平方根」が現れてくることになる。
実際に前回の研究員の眼で紹介したラファエル・ボンベリ(Rafael Bombelli,)は、1572年に出版した著書『L'Algebra(代数学)』の中で、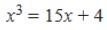 という方程式を例に挙げた。この方程式はx=4 を解に持っているが、カルダノの公式によれば、
という方程式を例に挙げた。この方程式はx=4 を解に持っているが、カルダノの公式によれば、
ところで、このカルダノの公式によれば、
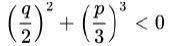 の時に負の数の平方根が現れる形になる。一方で、これは先に述べた三次方程式の判別式D>0の場合に相当していることから、相異なる3個の実数解を持つ条件に合致していることになる。即ち、実数解しかないにもかかわらず、カルダノの公式では「負の数の平方根」が現れてくることになる。
の時に負の数の平方根が現れる形になる。一方で、これは先に述べた三次方程式の判別式D>0の場合に相当していることから、相異なる3個の実数解を持つ条件に合致していることになる。即ち、実数解しかないにもかかわらず、カルダノの公式では「負の数の平方根」が現れてくることになる。実際に前回の研究員の眼で紹介したラファエル・ボンベリ(Rafael Bombelli,)は、1572年に出版した著書『L'Algebra(代数学)』の中で、
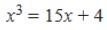 という方程式を例に挙げた。この方程式はx=4 を解に持っているが、カルダノの公式によれば、
という方程式を例に挙げた。この方程式はx=4 を解に持っているが、カルダノの公式によれば、
であることを示して、元の方程式が x = 4 を解に持つことを説明している5。
5 因みに、虚数単位iの知識がある今日の我々であれば、上式の左辺が右辺となることについては容易に確認できる。
また、因数分解を行うことで、残りの2つの解が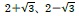 という実数解となることが確認できる。
という実数解となることが確認できる。
5 因みに、虚数単位iの知識がある今日の我々であれば、上式の左辺が右辺となることについては容易に確認できる。
また、因数分解を行うことで、残りの2つの解が
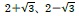 という実数解となることが確認できる。
という実数解となることが確認できる。四次方程式の解
についても、判別式等が存在して、その状況によって、4つの複素数解の状況(実数解と虚数解、解の重複度等)が異なってくる。
五次以上の方程式
n次方程式は、代数学の基本定理より、n個の複素数解を持つ。ただし、五次以上の一般の方程式に対する代数的解法は存在しない6。即ち、一般の五次方程式に対して代数的な解の公式は存在しない。これは、ノルウェーの数学者ニールス・アーベル(Niels Henrik Abel)7とイタリアの数学者パオロ・ルフィニ(Paolo Ruffini)らによって示され、「アーベル–ルフィニの定理(Abel–Ruffini theorem)」8と呼ばれている。
また、フランスの数学者エヴァリスト・ガロア(Évariste Galois)は、群や体の概念を使用することで、その証明を大幅に簡略化するとともに、方程式が代数的に解ける条件を裏付けている(現代において「ガロア理論(Galois theory)」と呼ばれる新しい数学の概念を導入している)。
6 五次方程式も(代数的ではないが)楕円関数等を用いた解の公式は存在している。
7 顕著な業績をあげた数学者に対して贈られる「アーベル賞」(2001年にアーベルの生誕200年を記念して創設された)にその名が冠せられている。数学における賞としては「フィールズ賞」が有名だが、これは4年に1回、40歳以下の数学者のみが対象となるのに対して、アーベル賞は、1年に1度で、年齢は問わず、賞金額も高額で、フィールズ賞よりもノーベル賞に近いものになっている。映画『ビューティフル・マインド』で描かれた米国の数学者ジョン・ナッシュ(John Forbes Nash Jr.)は、ゲーム理論の経済学への応用に関する貢献で、1994年にノーベル経済学賞を受賞しているが、さらに非線形偏微分方程式論とその幾何解析への応用に関する貢献で、2015年にアーベル賞を受賞している。なお、2025年には柏原正樹京都大学名誉教授が日本人として初めてアーベル賞を受賞している。
8 パオロ・ルフィ二の証明は完全ではなく、アーベルが初めて正確な証明を与えたとされているが、ルフィニは方程式の問題を群論の問題としてアプローチした先駆者として、重要な貢献をしている。
また、フランスの数学者エヴァリスト・ガロア(Évariste Galois)は、群や体の概念を使用することで、その証明を大幅に簡略化するとともに、方程式が代数的に解ける条件を裏付けている(現代において「ガロア理論(Galois theory)」と呼ばれる新しい数学の概念を導入している)。
6 五次方程式も(代数的ではないが)楕円関数等を用いた解の公式は存在している。
7 顕著な業績をあげた数学者に対して贈られる「アーベル賞」(2001年にアーベルの生誕200年を記念して創設された)にその名が冠せられている。数学における賞としては「フィールズ賞」が有名だが、これは4年に1回、40歳以下の数学者のみが対象となるのに対して、アーベル賞は、1年に1度で、年齢は問わず、賞金額も高額で、フィールズ賞よりもノーベル賞に近いものになっている。映画『ビューティフル・マインド』で描かれた米国の数学者ジョン・ナッシュ(John Forbes Nash Jr.)は、ゲーム理論の経済学への応用に関する貢献で、1994年にノーベル経済学賞を受賞しているが、さらに非線形偏微分方程式論とその幾何解析への応用に関する貢献で、2015年にアーベル賞を受賞している。なお、2025年には柏原正樹京都大学名誉教授が日本人として初めてアーベル賞を受賞している。
8 パオロ・ルフィ二の証明は完全ではなく、アーベルが初めて正確な証明を与えたとされているが、ルフィニは方程式の問題を群論の問題としてアプローチした先駆者として、重要な貢献をしている。
その他の性質等
実数係数のn次方程式 に関して,zが解なら、その共役複素数も解となる。
に関して,zが解なら、その共役複素数も解となる。
これは、前回の研究員の眼で紹介した共役複素数の性質に基づけば、容易に証明できる。
 に関して,zが解なら、その共役複素数も解となる。
に関して,zが解なら、その共役複素数も解となる。これは、前回の研究員の眼で紹介した共役複素数の性質に基づけば、容易に証明できる。
最後に
虚数及び複素数を巡る話題について、複数回に分けて報告することにしているが、今回は、複素数が数学の世界において、どのように有効に利用されているのかということで、方程式に関係するトピックについて説明した。
複素数の存在によって、代数学の世界が飛躍的に進展してきたことになる。
次回は、虚数や複素数が日常生活の中等でどのように使用されているのかについて報告する。
複素数の存在によって、代数学の世界が飛躍的に進展してきたことになる。
次回は、虚数や複素数が日常生活の中等でどのように使用されているのかについて報告する。
(2025年05月28日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
| 2025/09/25 | 数字の「49」に関わる各種の話題-49という数字に皆さんはどんなイメージを有しているのだろう- | 中村 亮一 | 研究員の眼 |
| 2025/09/12 | 数字の「48」に関わる各種の話題-48という数字は、結構いろいろな場面で現れてくるようだ- | 中村 亮一 | 研究員の眼 |
新着記事
-
2025年10月15日
「生活の質」と住宅価格の関係~教育サービス・治安・医療サービスが新築マンション価格に及ぼす影響~ -
2025年10月15日
IMF世界経済見通し-世界成長率見通しは3.2%まで上方修正 -
2025年10月15日
中国の物価関連統計(25年9月)~コアCPIの上昇率が引き続き拡大 -
2025年10月15日
芝浦電子の公開買付け-ヤゲオのTOB成立 -
2025年10月15日
英国雇用関連統計(25年9月)-週平均賃金は前年比5.0%まで再び上昇
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【複素数について(その2)-複素数と方程式-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
複素数について(その2)-複素数と方程式-のレポート Topへ




















 )として
)として






 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




