- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 平均と代表値の概念
コラム
2022年05月02日
文字サイズ
- 小
- 中
- 大
はじめに
平均や代表値の概念がいくつかあることについては、これまでも数多くの書籍等で紹介されてきたので、ご存じの方も多いと思われるが、今回改めて、この話題を取り上げてみることにした。
一般的な3つの平均の概念
因みに、相乗平均は、対数の相加平均の指数関数であり、相乗平均の対数は対数の相加平均となる。また、調和平均は、逆数の相加平均の逆数であり、逆数の相加平均は調和平均の逆数となる。
なお、相加平均は、その平均からのズレを意味する「偏差」の合計が0になる値である。また、偏差の二乗の合計が最小になる値である(このようにして「中心」を求める手法を「最小二乗法」と呼んでいる)。
これらの3つの平均は、その幾何学等における重要性から、ピタゴラス派(ピタゴラスによって創設された古代ギリシアの哲学の一派)やそれ以降のギリシアの数学者によって研究されてきており、「ピタゴラス平均(Pythagorean means)」と呼ばれる。
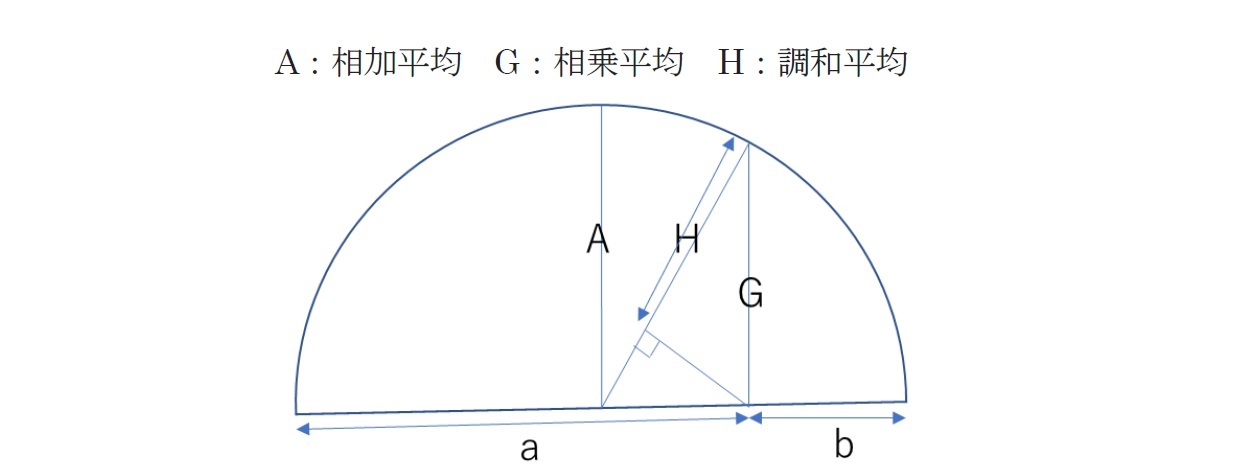
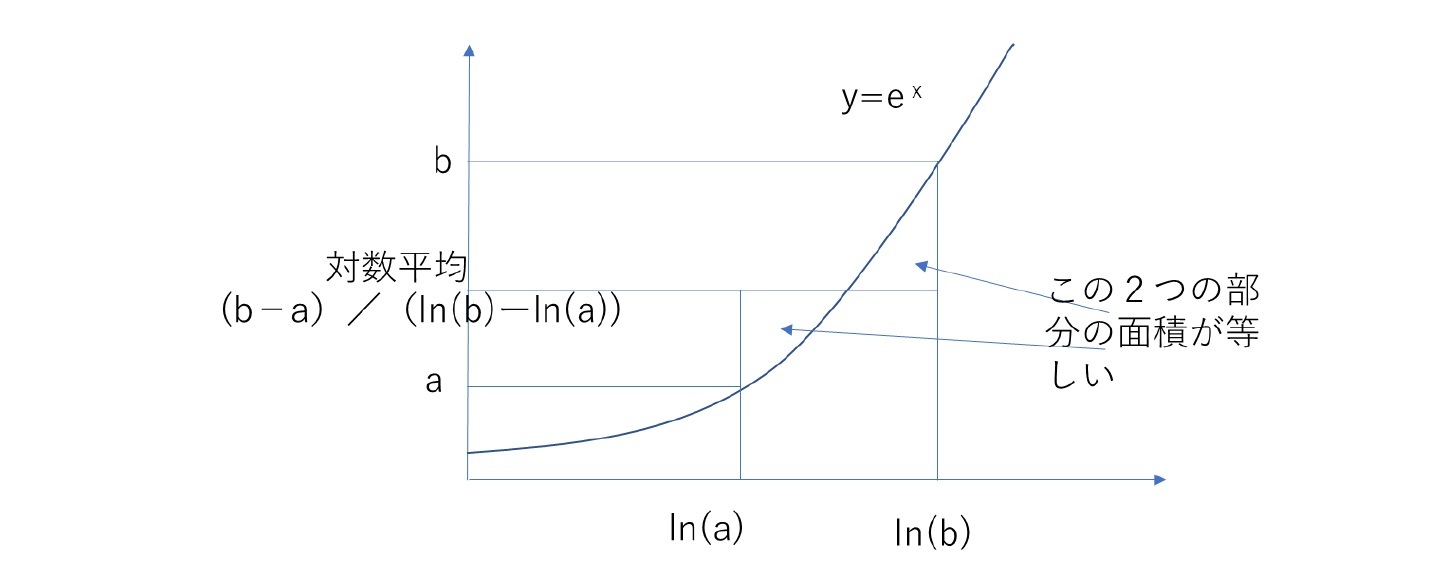
因みに、2つの数字aとbのピタゴラス平均は、以下の図で示すことができる。
なお、相加平均は、その平均からのズレを意味する「偏差」の合計が0になる値である。また、偏差の二乗の合計が最小になる値である(このようにして「中心」を求める手法を「最小二乗法」と呼んでいる)。
これらの3つの平均は、その幾何学等における重要性から、ピタゴラス派(ピタゴラスによって創設された古代ギリシアの哲学の一派)やそれ以降のギリシアの数学者によって研究されてきており、「ピタゴラス平均(Pythagorean means)」と呼ばれる。
因みに、2つの数字aとbのピタゴラス平均は、以下の図で示すことができる。
1 「average」の語源として、航路輸送中の積荷の損害を補てんするために「損害を平均的に負担する」(海上保険の起源)ことから、アラビア語で「損傷品」を意味する言葉から「平均」の意味が生まれた、とされているようだ。
一般化平均
この一般化平均において、p=1としたものが「相加平均」、p=-1としたものが「調和平均」、p→0の時の極限が「相乗平均」ということになる。また、p=2の場合は「二乗平均平方根(Root Mean Square:RMS)」、p=3の場合は「立法平均(Cubic mean)」と呼ばれる。さらに言えば、p→∞の時の極限が「最大値」、p→-∞の時の極限が「最小値」ということになる。
このように、上記で述べた各種の平均や最大値、最小値が1つの算式で表現される形になっている。こうした一般化ができることが、ある意味で、数学の面白さを表していると思われるが、皆さんは如何に感じられるだろうか。
このように、上記で述べた各種の平均や最大値、最小値が1つの算式で表現される形になっている。こうした一般化ができることが、ある意味で、数学の面白さを表していると思われるが、皆さんは如何に感じられるだろうか。
ここで、等号が成り立つのは。あくまでもx1=x2=・・・=xnの時に限る。
さらには、一般化平均については、p の広義増加関数(s < t ⇒ f(s) ≦ f(t))となっている。
さらには、一般化平均については、p の広義増加関数(s < t ⇒ f(s) ≦ f(t))となっている。
単純平均と加重平均
となる。なお、加重平均との関係では、通常の相加平均を「単純平均」ということがある。
日本の代表的な株式指数として、日経平均株価とTOPIX(東証株価指数)があるが、前者が株価「単純平均」指数2であるのに対し、後者は時価総額「加重平均」指数となっている。
2 なお、単純平均株価は、株式分割等による株価の権利落ち等が生じた場合に株価の連続性が保たれなくなるため、実際の平均株価の算出においては、除数を用いて、それを変化させて修正した平均株価が採用されている。例えば、米国の「ダウ平均株価(DJIA)」はダウ式平均という平均方法が採用されている。
日本の代表的な株式指数として、日経平均株価とTOPIX(東証株価指数)があるが、前者が株価「単純平均」指数2であるのに対し、後者は時価総額「加重平均」指数となっている。
2 なお、単純平均株価は、株式分割等による株価の権利落ち等が生じた場合に株価の連続性が保たれなくなるため、実際の平均株価の算出においては、除数を用いて、それを変化させて修正した平均株価が採用されている。例えば、米国の「ダウ平均株価(DJIA)」はダウ式平均という平均方法が採用されている。
なお、以下の大小関係が成り立つ。
算術平均≧対数平均≧幾何平均
算術平均≧対数平均≧幾何平均
各種の平均の使い分け
それでは、これらの平均の概念は、どのように使い分けられるのだろうか。一般的な考え方を整理すると以下の通りとなる。
「相加平均」は、対象データを足し合わせることで基準となる値が算出される場合に使用される。例えば、あるクラスにおける特定科目のテストの平均点やある会社の営業部全体の平均売上高等を算出する場合に使用される。
「相乗平均」は、対象データを掛け合わせることで基準となる値が算出される場合に使用される。例えば、過去の一定期間における売上高や人口等の指標の平均増加率を算出する場合(毎年の増加率そのものに意味があるのではなく、ある時点を基準とした場合の増加率に意味がある)に使用される。
「調和平均」は、対象データの逆数を足し合わせることで基準となる値が算出される場合に使用される。例えば、往路と復路の平均速度等を算出する場合(速度自体の足し算に意味はないが、速度の逆数は単位距離を進むのに必要な時間を表すことになり、その足し算は意味を有することになる)に使用される。さらに、複数の電気抵抗を並列に接続した場合の抵抗の算出にも使用される(因みに、これらを直列に接続した場合には相加平均となる)。
「加重平均」は、対象データに一定の重みを乗じてから足し合わせることにより、基準となる値が算出される場合で、世帯主の年齢階層別の平均貯蓄額から全世帯の平均貯蓄額を算出する場合(単純平均では、それぞれの階層の世帯数が反映されずに、全世帯の平均が計算できない)等に使用される。
「二乗平均平方根」は、データ値の二乗を取ることで、その量の大きさの平均値を二乗平均平方根から算出する。二乗することで、ある意味での重み付けをした形になっている。物理学や電子工学において、波動の振幅評価や、交流電流の実効値の算出、品質管理の公差解析等に使用される。また、光の強度は電磁場の振幅の二乗に比例し、その平均強度は二乗平均平方根で算出される。
「立法平均」は、機械部品の平均余命を予測するために使用される。
「対数平均」は、入口と出口で熱媒との温度差が異なる条件における熱交換器の熱量計算に使われる。円管を通しての熱伝導は、管の両側の温度差と管の厚みから計算される温度勾配が、円管内側と外側の面積の対数平均の面積を伝わっていると考えることができ、管内流れの代表温度差が入口温度差と出口温度差の対数平均を使って表される。
ただし、どの平均を使用するのが適当なのかについては、人間の感覚と関係している要素もあることから、一概には言えないところもある。最も一般的な考え方として「相加平均」を使用していても、実はその数値が人間の感覚にはマッチせず、より低い平均がイメージされて、「相乗平均」や「調和平均」を使用した方がしっくりするというケースもある。
「相加平均」は、対象データを足し合わせることで基準となる値が算出される場合に使用される。例えば、あるクラスにおける特定科目のテストの平均点やある会社の営業部全体の平均売上高等を算出する場合に使用される。
「相乗平均」は、対象データを掛け合わせることで基準となる値が算出される場合に使用される。例えば、過去の一定期間における売上高や人口等の指標の平均増加率を算出する場合(毎年の増加率そのものに意味があるのではなく、ある時点を基準とした場合の増加率に意味がある)に使用される。
「調和平均」は、対象データの逆数を足し合わせることで基準となる値が算出される場合に使用される。例えば、往路と復路の平均速度等を算出する場合(速度自体の足し算に意味はないが、速度の逆数は単位距離を進むのに必要な時間を表すことになり、その足し算は意味を有することになる)に使用される。さらに、複数の電気抵抗を並列に接続した場合の抵抗の算出にも使用される(因みに、これらを直列に接続した場合には相加平均となる)。
「加重平均」は、対象データに一定の重みを乗じてから足し合わせることにより、基準となる値が算出される場合で、世帯主の年齢階層別の平均貯蓄額から全世帯の平均貯蓄額を算出する場合(単純平均では、それぞれの階層の世帯数が反映されずに、全世帯の平均が計算できない)等に使用される。
「二乗平均平方根」は、データ値の二乗を取ることで、その量の大きさの平均値を二乗平均平方根から算出する。二乗することで、ある意味での重み付けをした形になっている。物理学や電子工学において、波動の振幅評価や、交流電流の実効値の算出、品質管理の公差解析等に使用される。また、光の強度は電磁場の振幅の二乗に比例し、その平均強度は二乗平均平方根で算出される。
「立法平均」は、機械部品の平均余命を予測するために使用される。
「対数平均」は、入口と出口で熱媒との温度差が異なる条件における熱交換器の熱量計算に使われる。円管を通しての熱伝導は、管の両側の温度差と管の厚みから計算される温度勾配が、円管内側と外側の面積の対数平均の面積を伝わっていると考えることができ、管内流れの代表温度差が入口温度差と出口温度差の対数平均を使って表される。
ただし、どの平均を使用するのが適当なのかについては、人間の感覚と関係している要素もあることから、一概には言えないところもある。最も一般的な考え方として「相加平均」を使用していても、実はその数値が人間の感覚にはマッチせず、より低い平均がイメージされて、「相乗平均」や「調和平均」を使用した方がしっくりするというケースもある。
代表値
ここからは、代表値の話に移る。
「代表値(representative value)」というのは、まさに多くのデータを代表して、データ全体を把握するための値を指している。このうちの「データの中心」を表すための代表値としては、先に述べたいわゆる相加平均(算術平均)である「平均値」に加えて、「中央値(メジアン)(median)」や「最頻値(モード)(mode)」がある。「代表値」というのは、統計学でいうところの標本の分布の特徴を代表的に表す統計学上の値としての「要約統計量」を意味しており、平均値等はこれら要素の一部を構成していることになる(平均以外には、分散、標準偏差や歪度、尖度等の「要約統計量」がある)。
「平均値」は、先に述べた「相加平均」を指している。
「中央値」は、データを昇順もしくは降順に並べた上で真ん中の順位に位置する値を言う。因みにデータ数が奇数の場合には真ん中のデータが存在するが、データ数が偶数の場合には真ん中のデータが2つ存在することになるので、通常はそれらの2つを足して2で割ったものが中央値になる。
「最頻値」は、最も頻繁に出現する値を言う。因みに、最も頻出する値が複数ある場合、それら全てが最頻値となる。例えば、一様分布の場合には全ての値が最頻値になる。
「代表値(representative value)」というのは、まさに多くのデータを代表して、データ全体を把握するための値を指している。このうちの「データの中心」を表すための代表値としては、先に述べたいわゆる相加平均(算術平均)である「平均値」に加えて、「中央値(メジアン)(median)」や「最頻値(モード)(mode)」がある。「代表値」というのは、統計学でいうところの標本の分布の特徴を代表的に表す統計学上の値としての「要約統計量」を意味しており、平均値等はこれら要素の一部を構成していることになる(平均以外には、分散、標準偏差や歪度、尖度等の「要約統計量」がある)。
「平均値」は、先に述べた「相加平均」を指している。
「中央値」は、データを昇順もしくは降順に並べた上で真ん中の順位に位置する値を言う。因みにデータ数が奇数の場合には真ん中のデータが存在するが、データ数が偶数の場合には真ん中のデータが2つ存在することになるので、通常はそれらの2つを足して2で割ったものが中央値になる。
「最頻値」は、最も頻繁に出現する値を言う。因みに、最も頻出する値が複数ある場合、それら全てが最頻値となる。例えば、一様分布の場合には全ての値が最頻値になる。
3つの代表値の比較
上記の3つの代表値を比較すると、以下の通りになっている。
・平均値は、全てのデータを反映できるが、中央値や最頻値は全てのデータを十分に考慮できない。
・平均値は外れ値(他の値から大きく外れた値)の影響を大きく受けることがあるが、標本数が少ない場合を除けば、中央値や最頻値は外れ値の影響を受けにくい。
なお、「平均値」は、先の「相加平均」の説明において述べたように、各種の有用な数学的性質(偏差の合計が0になる、偏差の二乗の合計が最小になる値である)を有している。さらに、平均値は全てのデータを反映していることから、一部のデータの変化に対しても、その変化が反映されるが、中央値や最頻値は変化しないこともある。このため、データの特性を把握するためにデータの分析を行う「統計学」においては、基本的には平均値が使用され、中央値や最頻値は平均値が有する弱点を補完する意味合いで使用されることになる。
また、「中央値」は、その値からのズレの絶対値の合計が最小となるような値となっている。その意味では、ある種の「中心」を示していることになる。ただし、例えば、平均値や最頻値の概念は2次元空間等でも考慮できるが、中央値の概念はそのままでは適用できず、一般化された概念が必要になってくる。
一方で、「最頻値」については、アンケートによって得られる結果や人の性というような「名義尺度」と呼ばれる数値以外のデータを取り扱う場合に、(平均値や中央値を算出できないことから)有用になってくる。
・平均値は、全てのデータを反映できるが、中央値や最頻値は全てのデータを十分に考慮できない。
・平均値は外れ値(他の値から大きく外れた値)の影響を大きく受けることがあるが、標本数が少ない場合を除けば、中央値や最頻値は外れ値の影響を受けにくい。
なお、「平均値」は、先の「相加平均」の説明において述べたように、各種の有用な数学的性質(偏差の合計が0になる、偏差の二乗の合計が最小になる値である)を有している。さらに、平均値は全てのデータを反映していることから、一部のデータの変化に対しても、その変化が反映されるが、中央値や最頻値は変化しないこともある。このため、データの特性を把握するためにデータの分析を行う「統計学」においては、基本的には平均値が使用され、中央値や最頻値は平均値が有する弱点を補完する意味合いで使用されることになる。
また、「中央値」は、その値からのズレの絶対値の合計が最小となるような値となっている。その意味では、ある種の「中心」を示していることになる。ただし、例えば、平均値や最頻値の概念は2次元空間等でも考慮できるが、中央値の概念はそのままでは適用できず、一般化された概念が必要になってくる。
一方で、「最頻値」については、アンケートによって得られる結果や人の性というような「名義尺度」と呼ばれる数値以外のデータを取り扱う場合に、(平均値や中央値を算出できないことから)有用になってくる。
3つの代表値の関係
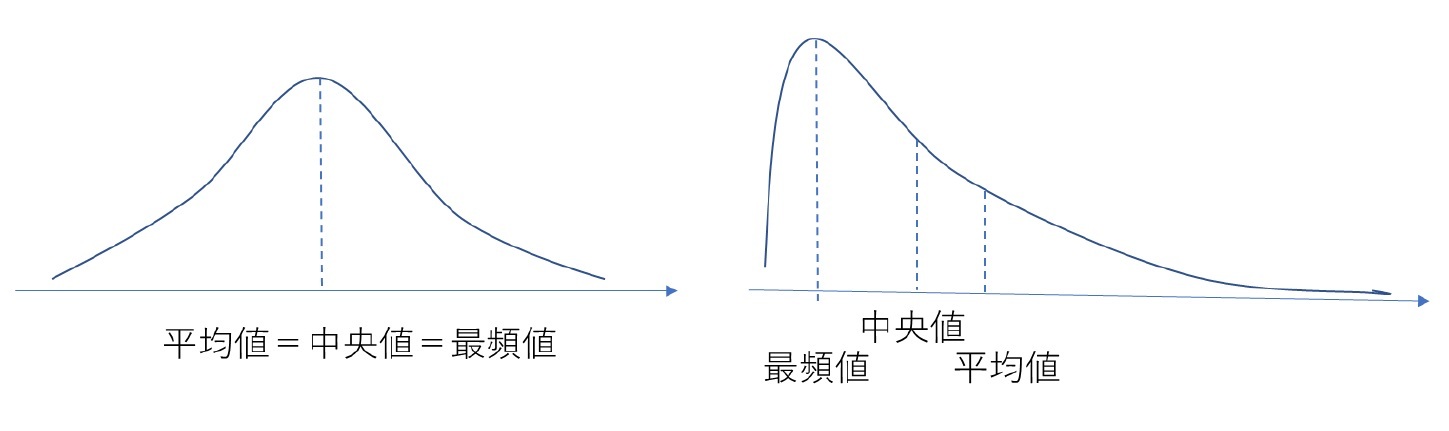
データの分布と3つの代表値の関係を見ると、以下のようになっている。なお、横軸がデータの値、縦軸がそれらの頻度を表している。
・分布が対称的で山が1つ(単峰性分布)の場合、3つの代表値は一致する。統計学の基本的な分布「正規分布」がまさにこれに該当する形になる。
・分布が対称的でも山が複数ある場合、平均値と中央値はほぼ同じになるが、最頻値は少なくとも2つある山に対応する値となる。
・分布が対称的でなく、山が1つの場合、最頻値はその山に対応する値となる。なお、「カール・ピアソンの経験則」と呼ばれるものがあり、「連続な単峰性分布では、経験則として、平均値から最頻値の方に3分の1ほどのところに中央値があり、式で表すと『中央値 ≈(2 × 平均値+最頻値)/3』となる。」とされているが、これは常に正しいわけではなく、実際には3つの代表値の順序は様々となる。
・なお、「単峰性分布では、最頻値は平均値から標準偏差の√3の範囲内にあり、最頻値の二乗平均偏差は標準偏差と標準偏差の2倍の間にある。」とされている。
分布の非対称性を示す「歪度」が高い分布として、有名なものに所得分布がある。大多数の所得がそれほど高くなくても、少数の高所得者や極少数の超高所得者の存在により、平均年収が大きく嵩上げされる形になる。
・分布が対称的で山が1つ(単峰性分布)の場合、3つの代表値は一致する。統計学の基本的な分布「正規分布」がまさにこれに該当する形になる。
・分布が対称的でも山が複数ある場合、平均値と中央値はほぼ同じになるが、最頻値は少なくとも2つある山に対応する値となる。
・分布が対称的でなく、山が1つの場合、最頻値はその山に対応する値となる。なお、「カール・ピアソンの経験則」と呼ばれるものがあり、「連続な単峰性分布では、経験則として、平均値から最頻値の方に3分の1ほどのところに中央値があり、式で表すと『中央値 ≈(2 × 平均値+最頻値)/3』となる。」とされているが、これは常に正しいわけではなく、実際には3つの代表値の順序は様々となる。
・なお、「単峰性分布では、最頻値は平均値から標準偏差の√3の範囲内にあり、最頻値の二乗平均偏差は標準偏差と標準偏差の2倍の間にある。」とされている。
分布の非対称性を示す「歪度」が高い分布として、有名なものに所得分布がある。大多数の所得がそれほど高くなくても、少数の高所得者や極少数の超高所得者の存在により、平均年収が大きく嵩上げされる形になる。
最後に
今回は、平均や代表値の概念について、述べてきた。
多くの方々にとって、日常生活の中では、相加平均や加重平均以外の平均の概念については、直接的にはあまり馴染みがないものかもしれない。ただし、理工系の学生や技術系の職務に関係している方々にとっては、どの平均の概念を使用するのかは大きな意味合いを有していて、その意義を十分に理解しておくことが求められる。また、経済学等の社会科学系の職務においても、相乗平均等が幅広く使用されている。
繰り返しになるが、多くの方々は、既に各種の経験を踏まえて、これらの各種の平均や代表値をどのように使い分けるべきなのかについて、一定程度の認識に基づいて、適切に行ってきているものと思われる。ただし、今回の研究員の眼で改めて、各種の平均や代表値の使い分けについて、再認識いただければと思った次第である。
多くの方々にとって、日常生活の中では、相加平均や加重平均以外の平均の概念については、直接的にはあまり馴染みがないものかもしれない。ただし、理工系の学生や技術系の職務に関係している方々にとっては、どの平均の概念を使用するのかは大きな意味合いを有していて、その意義を十分に理解しておくことが求められる。また、経済学等の社会科学系の職務においても、相乗平均等が幅広く使用されている。
繰り返しになるが、多くの方々は、既に各種の経験を踏まえて、これらの各種の平均や代表値をどのように使い分けるべきなのかについて、一定程度の認識に基づいて、適切に行ってきているものと思われる。ただし、今回の研究員の眼で改めて、各種の平均や代表値の使い分けについて、再認識いただければと思った次第である。
(2022年05月02日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
| 2025/09/25 | 数字の「49」に関わる各種の話題-49という数字に皆さんはどんなイメージを有しているのだろう- | 中村 亮一 | 研究員の眼 |
新着記事
-
2025年10月22日
高市新政権が発足、円相場の行方を考える~マーケット・カルテ11月号 -
2025年10月22日
貿易統計25年9月-米国向け自動車輸出が数量ベースで一段と落ち込む。7-9月期の外需寄与度は前期比▲0.4%程度のマイナスに -
2025年10月22日
米連邦地裁、Googleへの是正措置を公表~一般検索サービス市場における独占排除 -
2025年10月21日
選択と責任──消費社会の二重構造(2)-欲望について考える(3) -
2025年10月21日
連立協議から選挙のあり方を思う-選挙と同時に大規模な公的世論調査の実施を
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【平均と代表値の概念】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
平均と代表値の概念のレポート Topへ


















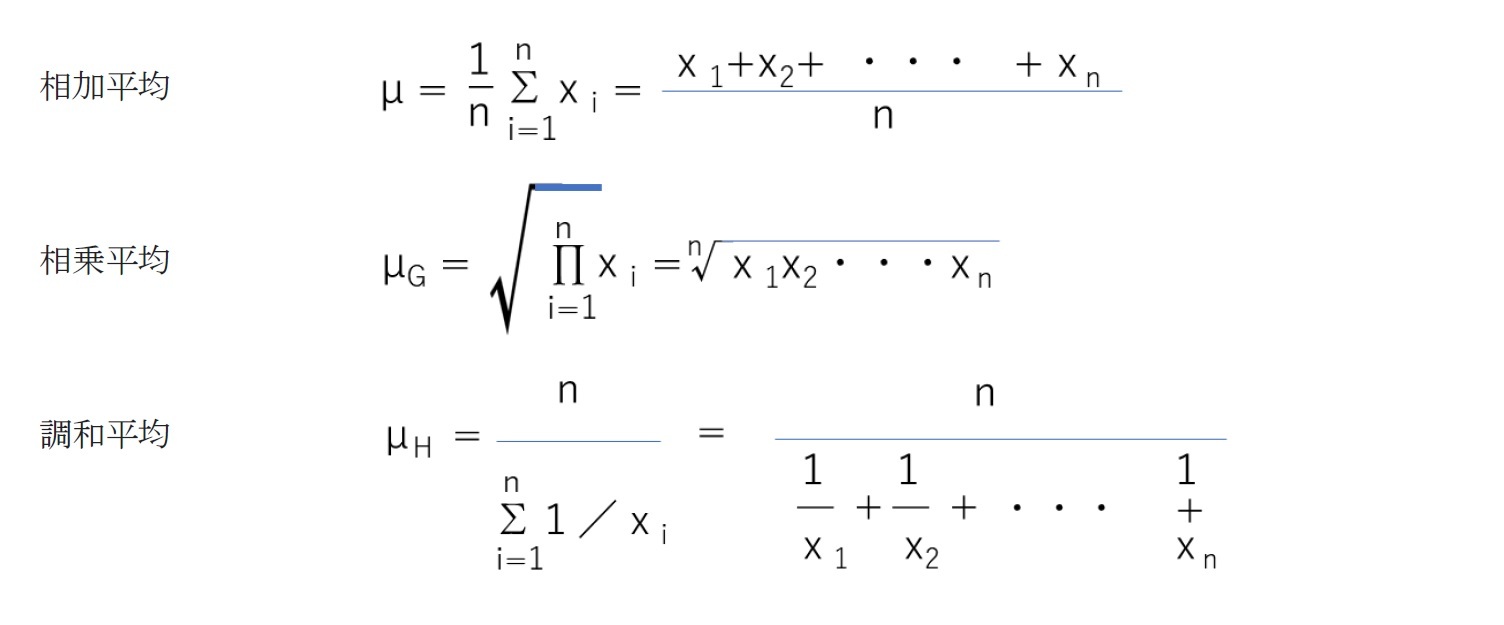

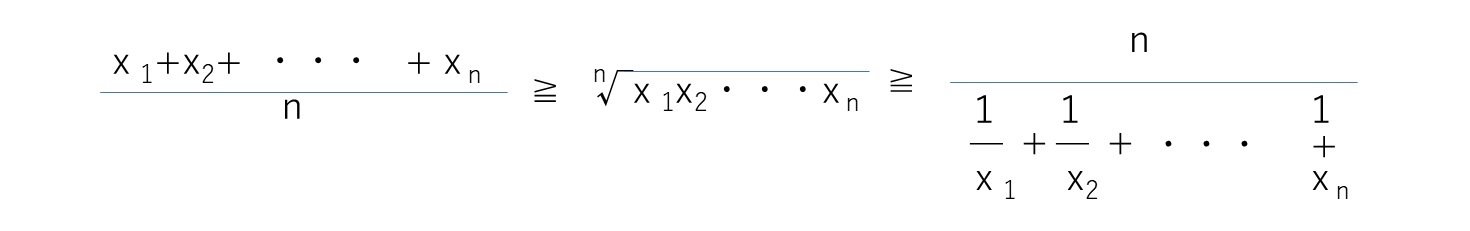

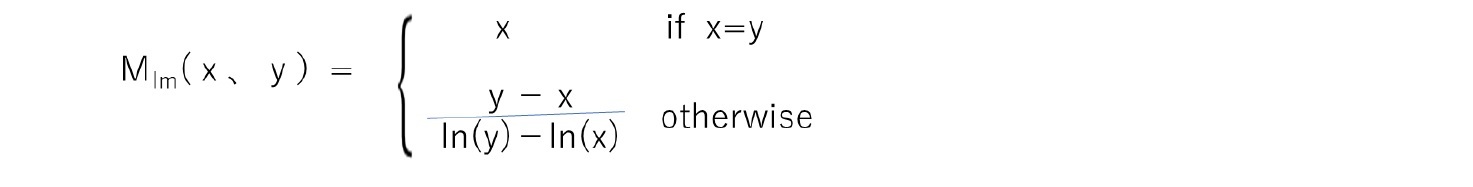

 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




