- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 誕生日が一致する確率-多くの人が集まる場では、誕生日の話題で盛り上がりませんか-

文字サイズ
- 小
- 中
- 大
はじめに
具体的には、(1)「(少なくとも2人1組ではなくて)2組以上のペアの誕生日が一致している確率」はどうなるのか、(2)「3人以上の誕生日が一致している確率」はどうなるのか、という問題である。
これからの年末年始の時期等に、多くの人が集まる場で話題にでもしてもらえればと思って、このトピックを採り上げることにした。
問題の設定
問題(その1)
問題1 部屋の中の全員の誕生日が異なる確率 P0
問題2 (部屋の中の誰でもよいので)最低1組2人のペアの誕生日が一致している確率 Q1
(ここでは、3人以上の誕生日が一致している場合は、含まれないとする。以下、同様)
問題4 最低2組のペアの誕生日が一致している確率 Q2
問題5 丁度2組4人のペアの誕生日が一致している確率 P2
問題6 最低3組のペアの誕生日が一致している確率 Q3
問題7 丁度3組のペアの誕生日が一致している確率 P3
以下、同様に、丁度k組の2人ずつのペアの誕生日が一致している確率Pkや最低k組のペアの誕生日が一致している確率Qkが考えられる。この場合、
となる。
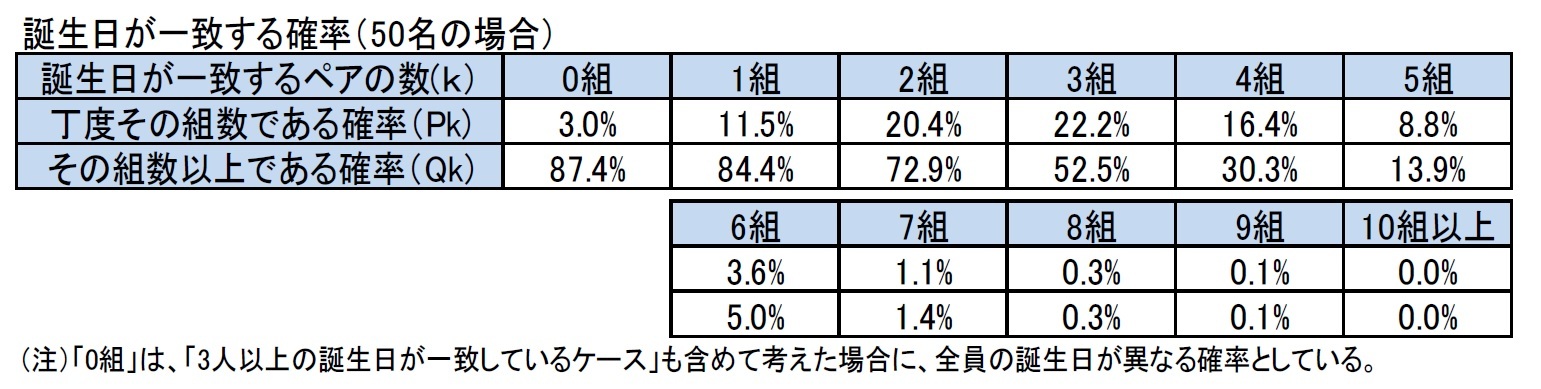
(1)全員の誕生日が異なる確率は「0組」の数の3.0%であることから、少なくとも誰かと誰かの誕生日が一致している確率は97.0%となる。
(2)誕生日が一致するペアの数としては、「3組」が最も多い。
(3)さすがに7組以上のペアが発生する確率は1.4%と低くなるが、それでも5組のペアが発生する確率は8.8%もあり、6組のペアが発生する確率も3.6%ある。
(4)一方で、全く誕生日が一致しないか、1組2人のペアの誕生日しか一致しない確率は、わずか14.5%(3.0%+11.5%)でしかない。このことはまた、誕生日が他の人と一致している人が3人以上(1組でも3人以上又は2組以上)いる確率は、85.5%ということになる。
(5)2組以上のペアが発生する確率は72.9%、3組以上のペアが発生する確率は52.5%となる。
(6)上記の表の0組以上の発生確率が87.4%となっているが、これと100%との差異の12.6%は、今回の計算で考慮されていない、「少なくとも3人以上の誕生日が一致している組が1つは存在している確率」となる。
(7)即ち、例えば、上記の表の「3組」には、「1組が3人の誕生日が一致、2組(あるいは3組)が2人の誕生日が一致」しているケース等は含まれていない。こうしたケースを含めれば、上記の表の確率はさらに高くなることになる。
(8)因みに、上記の表に基づくと、誕生日が一致するペアの数の期待値は、2.6組ということになる。50人いれば、平均して2.6組のペアの誕生日が一致していることになる。(7)で述べた3人以上の誕生日が一致しているケースも含めれば、さらに高い期待値になる。
50人のグループで考えても、例えば誕生日が一致しているペアが5組あることも決して珍しくない、ということになる。
なお、上に述べたように、「少なくとも3人以上の誕生日が一致している組が1つは存在している確率」は12.6%であるが、これが「少なくとも4人以上の誕生日が一致している組が1つは存在している確率」となると1%未満でぐっと小さくなる。一定数の組のペアが一致しているケースに比べて、一定人数の誕生日が一致するケースは、より発生が限られている。
(2016年12月19日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
| 2025/09/25 | 数字の「49」に関わる各種の話題-49という数字に皆さんはどんなイメージを有しているのだろう- | 中村 亮一 | 研究員の眼 |
新着記事
-
2025年10月16日
EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- -
2025年10月16日
再び不安定化し始めた米中摩擦-経緯の振り返りと今後想定されるシナリオ -
2025年10月15日
インド消費者物価(25年10月)~9月のCPI上昇率は1.5%に低下、8年ぶりの低水準に -
2025年10月15日
「生活の質」と住宅価格の関係~教育サービス・治安・医療サービスが新築マンション価格に及ぼす影響~ -
2025年10月15日
IMF世界経済見通し-世界成長率見通しは3.2%まで上方修正
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【誕生日が一致する確率-多くの人が集まる場では、誕生日の話題で盛り上がりませんか-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
誕生日が一致する確率-多くの人が集まる場では、誕生日の話題で盛り上がりませんか-のレポート Topへ



















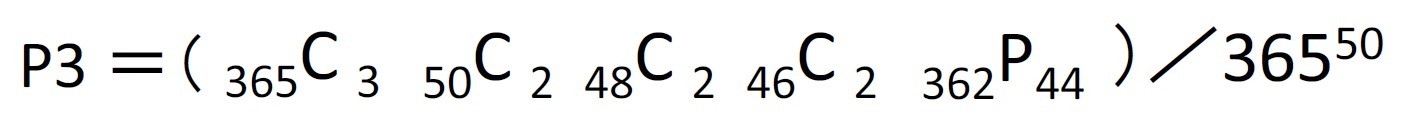

 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




