テニスの勝利確率－バレーボール、卓球、バドミントンに比べて番狂わせが少ないわけ

保険研究部主席研究員兼気候変動リサーチセンターチーフ気候変動アナリスト兼ヘルスケアリサーチセンター主席研究員篠原拓也

このレポートの関連カテゴリ

秋の季節は、いろいろなスポーツが花盛りだ。特に、点をとったりとられたりする球技は、試合中の情勢がわかりやすく、観客が盛り上がりやすい。

球技には、大きく分けて2つのタイプがある。1つは、野球、サッカー、ラグビーのように、1プレイごとに対戦しているどちらかのチームに点が入るとは限らないもの。もう1つは、テニス、バレーボール、卓球、バドミントンのように、1プレイごとに必ず対戦しているプレーヤーやチームのどちらかに点が入るタイプだ。このタイプは「ラリーポイント制」と呼ばれ、ある点数に到達すると、セットやゲームを獲得する。そして、獲得したセットやゲームがある数に達すると、試合に勝利する。

少し細かい点だが、テニスの場合、ファーストサービスのフォルトは1プレイとみなさず、ダブルフォルトになったときに1プレイとみなす。また、テニスでは、ふつうは1点、2点、3点といわずに、15点、30点、40点というが、ややこしくなるので、ここでは1点、2点、3点と表すことにする。

テニスは、点数カウントの仕組みが複雑だ。先に4点を獲得したプレーヤーがゲームを取る。そして、先に6ゲームを獲得したプレーヤーが、セットを取る。ただし、ゲームカウントが5-5で並んだ場合は、ゲームを2つ立て続けにとって7-5にするか、もしくは、ゲームカウント6-6で並んでタイブレークという7点先取のゲームをとることで、そのセットを獲得できる。そして、3セットを先に獲得したプレーヤーが勝利する(5セットマッチの場合)。

ここで、デュースという点数カウントの仕組みがある。あるゲームで点数が3-3で並んだ場合は、2点差をつけて上回らないと、そのゲームを獲得できない。また、タイブレークにも、デュースがある。点数が6-6で並んだ場合は、2点差をつけて上回らないと、そのセットを獲得できない(※注)。デュースがあることで、試合の緊張感が高まり、1プレイごとに観客が大いに沸くこととなる。

(※注) 4大大会のシングルスの試合では、最終セットでゲームカウントが6-6で並んだ場合、決着のつけ方がそれぞれ異なる。全米大会は、通常のセットと同様、7点先取のタイブレーク。全豪大会は、10点先取のタイブレーク。全仏大会はタイブレークを行わずにどちらかが2ゲーム差をつけて相手を上回るまで試合が決着しない。全英大会は、以前は全仏大会と同じだったが、2019年から仕組みが変わった。2ゲーム差がつかないままゲームカウントが12-12で並んだ場合、7点先取のタイブレークで決着をつけることとなった。

なお、年間最終戦であるATPファイナルズ(男子)やWTAファイナルズ(女子)のシングルスは、3セットマッチで、最終セットは通常のセットと同様、7点先取のタイブレークで行われている。

実は、テニスの1ゲームのスコアは、確率的に計算できる。これは、1つのゲームを獲得するまでのプレイの回数が、「負の二項分布」と呼ばれる確率分布に従うためだ。これ以後、算式が出てきて、やや難解かもしれない。算式をとばして、後の【計算結果】まで進んでいただいても構わない。

たとえば、プレーヤーAとBが対戦するとしよう。1プレイでAが得点する確率を、pと置く。Aが得点できない確率(Bが得点する確率)は、(1-p)だ。それぞれのプレイでの得点は、過去のプレイの結果とは無関係に、独立に決まると想定する。

さて、Aが4-0のラヴゲームで、ゲームを獲得する確率はどれくらいか。これは、確率pが4回続けて起こるのだから、(pの4乗)となる。

Aが4-1のスコアでゲームを獲得する確率はどうか。Bが1点を取るのが、Aが0点、1点、2点、3点のときの4パターンある。したがって、4×(1-p)×(pの4乗)となる。

同様に、Aが4-2のスコアでゲームを獲得する確率は、10×{(1-p)の2乗}×(pの4乗)となる。ここで、10という数字は、Bが2点を取るパターンの数だ。

ややこしいのが、点数が3-3で並んで、デュースの末にAがゲームを獲得するケースだ。まず、点数が3-3になる確率は、先ほどまでと同じように、20×{(1-p)の3乗}×(pの3乗)となる。

これに、デュース後にAが2点差をつけてBを上回る確率をかける。

まず、Aが2点続けて取る確率は、(pの2乗)。デュース後の2つのプレイでAとBが1点ずつを取り合って、1回デュースに戻ってから、Aが2点続けて取る確率は、2p(1-p)×(pの2乗)となる。

2回デュースに戻ってから、Aが2点続けて取る確率は、［{2p(1-p)}の2乗］×(pの2乗)。

3回デュースに戻ってから、Aが2点続けて取る確率は、［{2p(1-p)}の3乗］×(pの2乗)……。

高校の数学で出てきた等比数列の和の計算法を使って、これらを足していく。初項は(pの2乗)、公比は2p(1-p)だ。その結果、デュース後にAが2点差をつけてBを上回る確率は、(pの2乗)÷{1-2p(1-p)}となる。

したがって、Aがデュースの末にゲームを獲得する確率は、以下のようになる。

20×{(1-p)の3乗}×(pの3乗)×(pの2乗)÷{1-2p(1-p)}

つまり、Aがゲームを取る確率は、4-0のラヴゲーム、4-1のスコア、4-2のスコア、デュースの末、のそれぞれでゲームを取る確率を、全部足し算して、

(pの4乗)＋4×(1-p)×(pの4乗)＋10×{(1-p)の2乗}×(pの4乗)＋20×{(1-p)の3乗}×(pの5 乗)÷{1-2p(1-p)}

となる。かなりごちゃごちゃしているが、pが決まれば、なんとか計算できるわけだ。

そして、これを何ゲームも繰り返していって、6つのゲームを取るとセットが得られ、獲得したセットの数が3つになると、試合に勝利することになる（5セットマッチの場合）。

【計算結果】
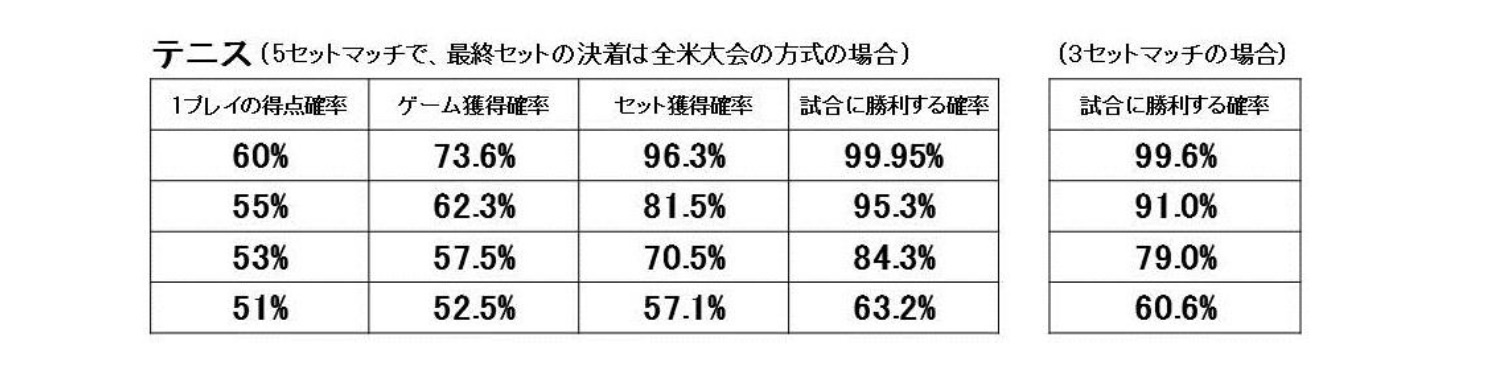
1プレイの得点確率に対して、ゲームやセットを取る確率、試合に勝つ確率はどれくらいなのか。1プレイの得点確率を60％、55％、53％、51％の4通りにおいた計算結果は、つぎの表のようになった。

1プレイの得点確率が60％ある場合(相手の得点確率が40％にとどまる場合)、ゲームを獲得する確率は73.6％、セットを獲得する確率は96.3％、そして5セットマッチの試合に勝利する確率は99.95％。

つまり、1プレイの得点確率が60％あると、ほぼ確実に試合に勝てる。この確率が55％や53％の場合でも、試合には95.3％や84.3％とかなり高い確率で勝てる。それどころか、両者がほぼ互角で、1プレイの得点確率が51％(相手の得点確率は49％)とわずかに相手を上回るような場合でも、試合に勝つ確率は63.2％とけっこう高い。

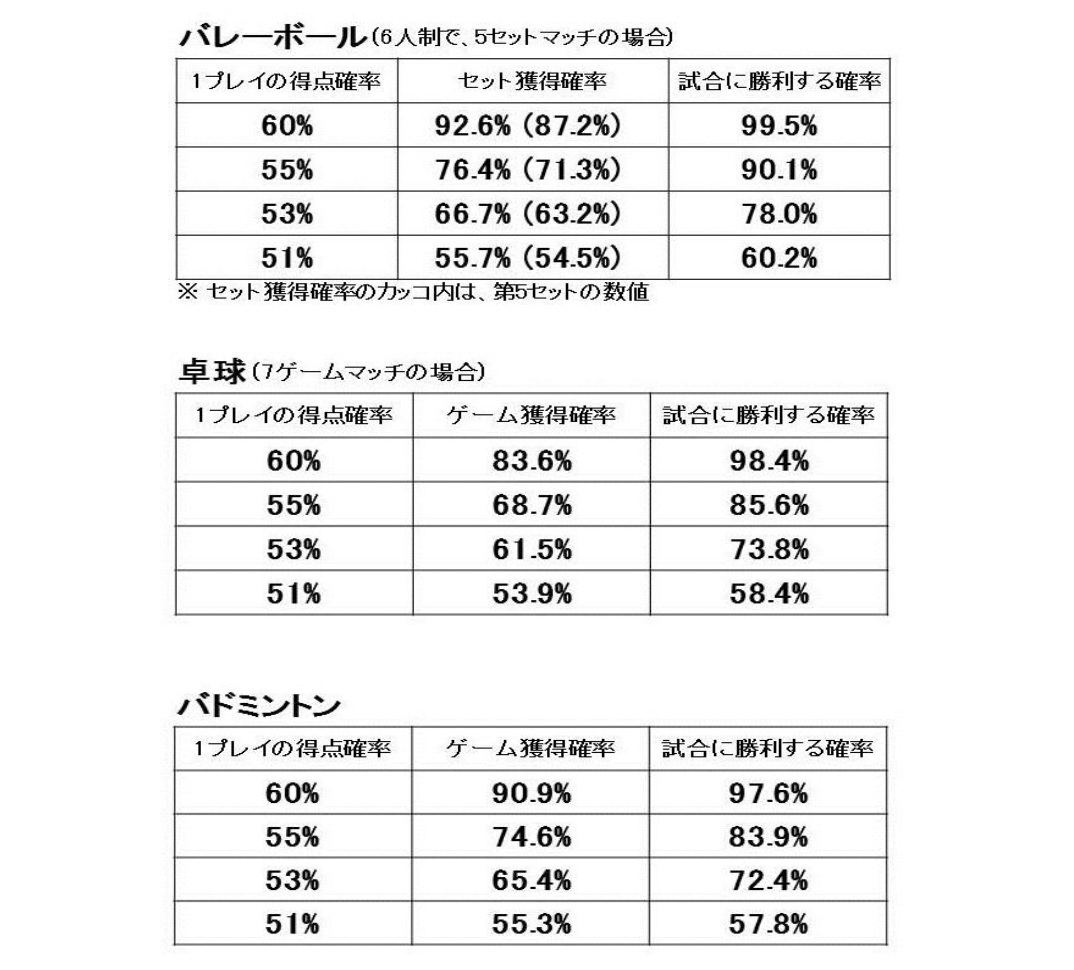
これをバレーボール(6人制、5セットマッチ)、卓球(7ゲームマッチ)、バドミントンと比較したい。ここで、それぞれの球技の点数カウントの仕組みについても、簡単にみておこう。

バレーボールは、先に25点を獲得したチームがセットを取る。ただし、点数が24-24で並んだ場合は、デュースとなって2点差をつけて相手を上回った場合にセットを取る。そして、先に3セットを獲得したチームが勝利する。

ただし、セットカウントが2-2で並んだ場合は、第5セットは、15点を獲得したチームがこのセットを取って試合に勝利する。なお、第5セットの点数が14-14で並んだ場合は、デュースとなって2点差をつけて相手を上回ったチームが試合に勝利する。

卓球は、先に11点を獲得したプレーヤーがゲームを取る。ただし、点数が10-10で並んだ場合は、デュースとなって2点差をつけて相手を上回った場合にゲームを取る。そして、先に4ゲームを獲得したプレーヤーが勝利する(7ゲームマッチの場合)。

バドミントンは、先に21点を獲得したプレーヤーがゲームを取る。ただし、点数が20-20で並んだ場合は、デュースとなって2点差をつけて相手を上回った場合にゲームを取る。なお、デュースが続いて点数が29-29で並んだ場合は、30点目の点を獲得したプレーヤーがゲームを取る。そして、先に2ゲームを獲得したプレーヤーが勝利する。

さて、4つの球技の計算結果を比べてみよう。1プレイの得点確率を55％とした場合、試合の勝利確率は、テニス(5セットマッチ)が95.3％なのに対し、バレーボールが90.1％。卓球が85.6％、そしてバドミントンが83.9％という結果となった。つまり、テニス、バレーボール、卓球、バドミントンの順番に、試合に勝利する確率が高いことになる。この順番は、1プレイの得点確率を60％、53％、51％にした場合も同じだ。

バレーボール・卓球・バドミントンで1プレイの得点確率に対して、ゲームやセットを取る確率、試合に勝つ確率

つまり、この4つの球技のなかで、テニスは、相手との1プレイの得点確率の差が、試合の勝敗にもっとも影響しやすいといえる。これは、劣勢とみられていたプレーヤーが勝つ、いわゆる“番狂わせ”が起きにくいともいえる。

最後に、1つ重要な注意点を述べる。今回取り上げた4つの球技では、サービスをするか、レシーブをするかで、1プレイの得点確率は全く違ったものになることが多い。特に、テニスはその傾向が顕著だ。しかし、上記の分析では計算が複雑になることを避けるために、サービスかレシーブかの違いは考慮せずに1プレイの得点確率を置いている。その点にご注意いただきたい。

こんどラリーポイント制の球技をプレイしたり、観戦したりするときには、得点のカウントの仕組みが試合に与える影響を、少し考えてみてはいかがだろうか。

日付	タイトル	執筆者	媒体
2025/03/25	産業クラスターを通じた脱炭素化－クラスターは温室効果ガス排出削減の潜在力を有している	篠原拓也	基礎研レター
2025/03/18	気候変動:アクチュアリースキルの活用－「プラネタリー・ソルベンシー」の枠組みに根差したリスク管理とは?	篠原拓也	基礎研レター
2025/03/11	国民負担率 24年度45.8%の見込み－高齢化を背景に、欧州諸国との差は徐々に縮小	篠原拓也	研究員の眼
2025/03/04	サイバーリスクのモデリング－相互に接続されたシステミックリスクをどうモデリングする?	篠原拓也	保険・年金フォーカス

日付

タイトル

執筆者

媒体

2025/03/25

産業クラスターを通じた脱炭素化－クラスターは温室効果ガス排出削減の潜在力を有している

篠原拓也

基礎研レター

2025/03/18

気候変動:アクチュアリースキルの活用－「プラネタリー・ソルベンシー」の枠組みに根差したリスク管理とは?

篠原拓也

基礎研レター