- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- パーティ問題又はラムゼー問題-混沌の中にも、一定のスケールがあれば、特定の秩序が現われるってこと知っていましたか-
コラム
2017年09月04日
文字サイズ
- 小
- 中
- 大
はじめに
皆さん、「パーティ問題」というのをご存知だろうか。政治家の行う政治資金調達のためのパーティー券の購入代金を巡る問題ではない。まさに、我々一般が日常生活において開催・参加する「パーティ」に絡む問題である。
今回の研究員の眼では、こうした「パーティ問題」と呼ばれるもののうち、「ラムゼー問題」と呼ばれるものを紹介する。
今回の研究員の眼では、こうした「パーティ問題」と呼ばれるもののうち、「ラムゼー問題」と呼ばれるものを紹介する。
ラムゼー問題
一般的に「ラムゼー問題」と呼ばれているものは、パーティを題材にして、
「パーティで6人が集まれば、お互いが知り合いである3人組か、お互いに知らない3人組、のいずれかが必ず存在することを証明せよ。」
という問題である。
これは、グラフ理論や組み合わせ理論において、非常に有名な問題である。一見すると必ずしも自明ではないと思われるが、結論はとても興味深いと感じられるのではないか。こうした考え方は、図表の彩色やデザイン等を考える上で応用されている。
「パーティで6人が集まれば、お互いが知り合いである3人組か、お互いに知らない3人組、のいずれかが必ず存在することを証明せよ。」
という問題である。
これは、グラフ理論や組み合わせ理論において、非常に有名な問題である。一見すると必ずしも自明ではないと思われるが、結論はとても興味深いと感じられるのではないか。こうした考え方は、図表の彩色やデザイン等を考える上で応用されている。
ラムゼー問題の証明
ラムゼー問題の証明はグラフを用いることで容易に理解されうる形で行える。
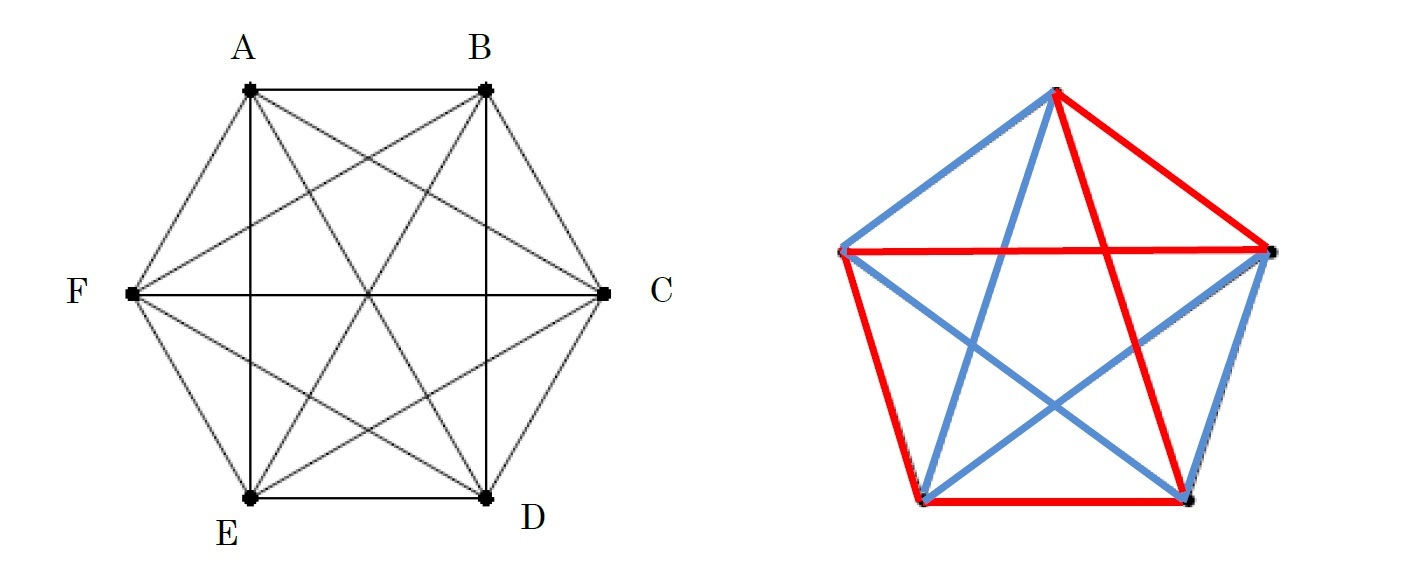
6人をそれぞれ点(A、B、C、D、E、F)で表すこととし、2人が知り合いであれば赤い線で、知り合いでなければ青い線で結ぶことにする。こうして作成されるグラフにおいて、赤い三角形または青い三角形が存在することを示せばよいことになる。
Aという点(人)に注目すると、この点からは5本の線が出ている。従って、赤い線か青い線のいずれかが少なくとも3本出ていることになる。ここでは、赤い線が3本でているとして、その相手をB、C、Dとする。すると、
BとCを結ぶ線が赤い線であれば、ABCが赤い三角形となる。
CとDを結ぶ線が赤い線であれば、ACDが赤い三角形となる。
BとDを結ぶ線が赤い線であれば、ABDが赤い三角形となる。
上記のいずれでもなければ、BCDが青い三角形となる。
となり、いずれのケースでも、赤い三角形または青い三角形が存在することになる。
何とも簡潔でわかりやすい証明ではないだろうか。
これを原始的に証明しようとすれば、6点を結ぶ線は全部で215(=32,768)通りあるので、これをチェックすればよいことになるが、これはかなりハードな仕事だろう。
6人をそれぞれ点(A、B、C、D、E、F)で表すこととし、2人が知り合いであれば赤い線で、知り合いでなければ青い線で結ぶことにする。こうして作成されるグラフにおいて、赤い三角形または青い三角形が存在することを示せばよいことになる。
Aという点(人)に注目すると、この点からは5本の線が出ている。従って、赤い線か青い線のいずれかが少なくとも3本出ていることになる。ここでは、赤い線が3本でているとして、その相手をB、C、Dとする。すると、
BとCを結ぶ線が赤い線であれば、ABCが赤い三角形となる。
CとDを結ぶ線が赤い線であれば、ACDが赤い三角形となる。
BとDを結ぶ線が赤い線であれば、ABDが赤い三角形となる。
上記のいずれでもなければ、BCDが青い三角形となる。
となり、いずれのケースでも、赤い三角形または青い三角形が存在することになる。
何とも簡潔でわかりやすい証明ではないだろうか。
これを原始的に証明しようとすれば、6点を結ぶ線は全部で215(=32,768)通りあるので、これをチェックすればよいことになるが、これはかなりハードな仕事だろう。
因みに、5人の場合には、上記の右図のように、赤い三角形も青い三角形も作らずにグラフを描くことができる。すなわち、どの3人の組み合わせをみても、知り合いや知り合いでない人だけの組み合わせは存在しないことになる。
ラムゼー問題の一般化、ラムゼーの定理、ラムゼー理論
実は、この問題はさらに一般化されて、「ラムゼーの定理」と呼ばれるものが存在する。
「完全グラフ」というのは、上記の図のように全ての頂点間が線で結ばれたグラフのことを言うが、頂点数がnの完全グラフを Knと表すことにする。この時、先のラムゼー問題の結論は、以下のように言い換えることができる。
「K6の各辺を青と赤の2色でどのように着色しても、赤い辺からなるK3か、青い辺からなるK3が部分グラフとして必ず含まれる。」
これを一般化することで、以下の「ラムゼーの定理」が得られる1。
「cとmを任意の自然数とするとき、次を満たす自然数nが存在する。
Knの各辺をc色でどのように着色しても、同じ色の辺からなるKmが部分グラフとして必ず含まれる。」
ラムゼーの定理をさらに一般化して応用する理論は「ラムゼー理論」と言われ、離散型数学のグラフ理論として、現在も数多くの数学者を魅了し、幅広い研究が行われている。
寺垣内政一広島大学大学院教授のペーパー「ラムゼー理論の話題から」によれば、「そのテーマは、粗っぽくいえば、混沌の規模がある程度大きくなると、その内部にある種の秩序が必然的に現われることを意味する。」とのことである。さらに、「いわゆるラムゼー数とよばれる値の決定は、グラフ理論における最難関の課題の1つ」であり、「もっとも単純な問題設定を描写すれば、どんな自然数Nに対しても、ある自然数R(N)が存在し、n≧R(N)ならば、n頂点完全グラフKnのすべての辺を赤か青でどのように色付けしても、赤辺だけでできたN頂点完全グラフKNか、青辺だけでできたKNが見つかる。」とされている。
再び、このことをパーティの問題に翻訳し直すと、知り合いを赤、知り合いでなければ青とすれば、
「パーティを開催する際に、少なくともN人がお互いに全員知り合いか、N人のお互いが全く知り合いでないグループを含むようにするには、最低R(N)人を招待すればよい。」ということになる。
さて、先の寺垣内氏のペーパーによれば、「このR(N)がラムゼー数とよばれており、ラムゼーの定理によってその値の存在は保証されている。しかし、R(3)=6、R(4)=18であることを確認するのは困難ではないが、R(5)の値はいまだ決定されていない。」ということである。
R(3)=6であることは、「ラムゼー問題の証明」の箇所で示した通りである。
なお、ラムゼー(Frank Ramsey)(1903~1930)は、英国の数学者、哲学者であるが、わずか26歳でこの世を去っている。
1 ここで述べている「ラムゼーの定理」も、単純化されたものであり、分かりやすい形で表現しているが、通常の「ラムゼーの定理」はさらに一般化されている。
「完全グラフ」というのは、上記の図のように全ての頂点間が線で結ばれたグラフのことを言うが、頂点数がnの完全グラフを Knと表すことにする。この時、先のラムゼー問題の結論は、以下のように言い換えることができる。
「K6の各辺を青と赤の2色でどのように着色しても、赤い辺からなるK3か、青い辺からなるK3が部分グラフとして必ず含まれる。」
これを一般化することで、以下の「ラムゼーの定理」が得られる1。
「cとmを任意の自然数とするとき、次を満たす自然数nが存在する。
Knの各辺をc色でどのように着色しても、同じ色の辺からなるKmが部分グラフとして必ず含まれる。」
ラムゼーの定理をさらに一般化して応用する理論は「ラムゼー理論」と言われ、離散型数学のグラフ理論として、現在も数多くの数学者を魅了し、幅広い研究が行われている。
寺垣内政一広島大学大学院教授のペーパー「ラムゼー理論の話題から」によれば、「そのテーマは、粗っぽくいえば、混沌の規模がある程度大きくなると、その内部にある種の秩序が必然的に現われることを意味する。」とのことである。さらに、「いわゆるラムゼー数とよばれる値の決定は、グラフ理論における最難関の課題の1つ」であり、「もっとも単純な問題設定を描写すれば、どんな自然数Nに対しても、ある自然数R(N)が存在し、n≧R(N)ならば、n頂点完全グラフKnのすべての辺を赤か青でどのように色付けしても、赤辺だけでできたN頂点完全グラフKNか、青辺だけでできたKNが見つかる。」とされている。
再び、このことをパーティの問題に翻訳し直すと、知り合いを赤、知り合いでなければ青とすれば、
「パーティを開催する際に、少なくともN人がお互いに全員知り合いか、N人のお互いが全く知り合いでないグループを含むようにするには、最低R(N)人を招待すればよい。」ということになる。
さて、先の寺垣内氏のペーパーによれば、「このR(N)がラムゼー数とよばれており、ラムゼーの定理によってその値の存在は保証されている。しかし、R(3)=6、R(4)=18であることを確認するのは困難ではないが、R(5)の値はいまだ決定されていない。」ということである。
R(3)=6であることは、「ラムゼー問題の証明」の箇所で示した通りである。
なお、ラムゼー(Frank Ramsey)(1903~1930)は、英国の数学者、哲学者であるが、わずか26歳でこの世を去っている。
1 ここで述べている「ラムゼーの定理」も、単純化されたものであり、分かりやすい形で表現しているが、通常の「ラムゼーの定理」はさらに一般化されている。
まとめ-ラムゼー理論等のグラフ理論の応用等-
以上、身近なパーティを題材にしたラムゼー問題から、より一般的なラムゼー理論について、簡単に紹介してきたが、結局ラムゼー理論とは、「完全な無秩序というものは存在せず、混沌としたものの中にも、一定のスケールがあれば、特定の秩序が現われる。」と解釈されることになるものと思われる。
こうしたラムゼー理論や様々なグラフ理論の考え方は、ネットワーク・電気回路等の数学的モデルとして利用されている他、ネットワークデザイン、ビジュアルインタフェースなど幅広い分野で応用されている。
この研究員の眼を1つの契機に、ラムゼー理論さらにはグラフ理論に少しは興味を抱いていただければと感じた次第である。
こうしたラムゼー理論や様々なグラフ理論の考え方は、ネットワーク・電気回路等の数学的モデルとして利用されている他、ネットワークデザイン、ビジュアルインタフェースなど幅広い分野で応用されている。
この研究員の眼を1つの契機に、ラムゼー理論さらにはグラフ理論に少しは興味を抱いていただければと感じた次第である。
(2017年09月04日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
新着記事
-
2025年10月24日
米連邦政府閉鎖と代替指標の動向-代替指標は労働市場減速とインフレ継続を示唆、FRBは政府統計を欠く中で難しい判断を迫られる -
2025年10月24日
企業年金の改定についての技術的なアドバイス(欧州)-EIOPAから欧州委員会への回答 -
2025年10月24日
消費者物価(全国25年9月)-コアCPI上昇率は拡大したが、先行きは鈍化へ -
2025年10月24日
保険業界が注目する“やせ薬”?-GLP-1は死亡率改善効果をもたらすのか -
2025年10月23日
御社のブランドは澄んでますか?-ブランド透明性が生みだす信頼とサステナビリティ開示のあり方(1)
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【パーティ問題又はラムゼー問題-混沌の中にも、一定のスケールがあれば、特定の秩序が現われるってこと知っていましたか-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
パーティ問題又はラムゼー問題-混沌の中にも、一定のスケールがあれば、特定の秩序が現われるってこと知っていましたか-のレポート Topへ



















 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




