- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- なぜ味噌汁は動くのか
NEW
コラム
2025年10月27日
文字サイズ
- 小
- 中
- 大
■要旨
「味噌汁が動いた」
日本の食卓で古くから見られる光景について、幼い息子から素朴な疑問が呈された。父親である研究員がこの世に生を受けておよそ半世紀、ついに味噌汁の謎に迫ることとした。
■目次
0――はじめに
1――物理の力なくして物は動かない
1|静止摩擦力
2|引き算の静止摩擦力
3|ボイル・シャルルの法則
4|味噌汁は「動く」ではなく「浮く」?
2――味噌汁が動くのを防ぐ工夫
3――その他の要因
1|テーブルの水の気化
2|液体の水という潤滑剤
4――まとめ
「味噌汁が動いた」
日本の食卓で古くから見られる光景について、幼い息子から素朴な疑問が呈された。父親である研究員がこの世に生を受けておよそ半世紀、ついに味噌汁の謎に迫ることとした。
■目次
0――はじめに
1――物理の力なくして物は動かない
1|静止摩擦力
2|引き算の静止摩擦力
3|ボイル・シャルルの法則
4|味噌汁は「動く」ではなく「浮く」?
2――味噌汁が動くのを防ぐ工夫
3――その他の要因
1|テーブルの水の気化
2|液体の水という潤滑剤
4――まとめ
0――はじめに
先日家族で食卓を囲んでいたところ、3歳の息子が「味噌汁が動いた!」と声を上げた。日本の食卓で古くから見られる光景である。「そうか。また、動いたか。」などと軽く捉えていたが、息子は年齢的にも「なんで?なんで?」を繰り返す時期である。当然に「なんで動くの?」という照会に接した。
1――物理の力なくして物は動かない
私も理系の端くれである。動く理由を説明するのにオカルトじみた未知なる力を引き合いに出すのは受け入れられない。高校時代に学習した物理の知識を動員し検討することとした。とはいえさすがに電気や磁気の力が働いているとは考えにくいため、力学・熱力学で説明ができるのではないかと当たりを付けた。また、思考実験にあたっては、「『熱い味噌汁が入ったお椀』が、『水でぬれたテーブルの上にある時』に動く」という経験則を前提とした。
1|静止摩擦力
通常、物体が水平に動かないのは「静止摩擦力」が原因である。静止摩擦力とは、物体が水平方向の力を受けた際に、動き出さないように留める抗力である。静止摩擦係数をμ'、物体の質量(重さ)をM、重力加速度をgとすると、静止摩擦力の最大値はμ'Mgとなる。これを超える力が水平方向に加わったとき、ついに物体は水平方向に動くのである。静止摩擦係数μ'は材質などで決まる比例定数のようだが、筆者はこの分野について専門外であり、詳細には踏み込めない。
通常、物体が水平に動かないのは「静止摩擦力」が原因である。静止摩擦力とは、物体が水平方向の力を受けた際に、動き出さないように留める抗力である。静止摩擦係数をμ'、物体の質量(重さ)をM、重力加速度をgとすると、静止摩擦力の最大値はμ'Mgとなる。これを超える力が水平方向に加わったとき、ついに物体は水平方向に動くのである。静止摩擦係数μ'は材質などで決まる比例定数のようだが、筆者はこの分野について専門外であり、詳細には踏み込めない。
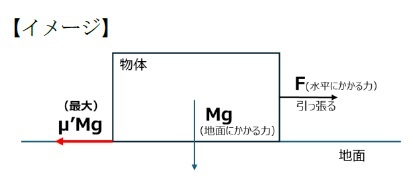 水平方向の力Fが、μ'Mgより小さい場合は、静止摩擦力により水平方向に動かないが、Fがμ'Mgを超えると、水平方向に動き出す。
水平方向の力Fが、μ'Mgより小さい場合は、静止摩擦力により水平方向に動かないが、Fがμ'Mgを超えると、水平方向に動き出す。数式を見ると難しく感じるが、単に「重いものほど動きにくい」、「ざらざらした地面(静止摩擦係数の大きい地面)ほど動きにくい」というだけのものだ。
しかし、そもそも味噌汁には水平方向の力が働いているのだろうか。食卓での味噌汁の挙動を見ると「何もしていないのに“つつつ”と動く」イメージだろう。なので「水平方向の力が、静止摩擦力を超えて加わったから動いた」というものでは説明がつかないように思える。
では、電気や磁気、果てはオカルト的な何かの力なのだろうか?
それでもなお、答えは「静止摩擦力」にあると考えた。
2|引き算の静止摩擦力
もしアイススケートのリンクのように、何もせずとも滑るような状態であれば、水平に動くための「水平方向の力」はほとんど不要になる。それこそ摩擦力さえなければ、テーブルのちょっとした傾きや、風などの些細な力で動くはずである。
すなわち「水平方向の力」で説明するのではなく、「静止摩擦力が小さくなることで味噌汁は勝手に動く」という説明である。まさに引き算の発想である。
静止摩擦力を振り返ってみると、静止摩擦係数(μ')と地面にかかる力(Mg)の掛け算となっている。この静止摩擦力の算式から、静止摩擦係数 μ' が小さくなるか、地面にかかる力 Mg が小さくなれば、味噌汁は動くはずである。
静止摩擦係数は、上述のとおり筆者は明るくない。「濡れたテーブル」ということで、水があることで一定程度係数が小さくなることは想像できるものの、それだけで動くのであれば味噌汁以外の食器もすべて動くはずである。なので今回はもう片方の「地面にかかる力」に着目し、味噌汁の挙動に迫りたい。おそらく味噌汁の「地面にかかる力」を小さくする『何か』があるはずである。
もしアイススケートのリンクのように、何もせずとも滑るような状態であれば、水平に動くための「水平方向の力」はほとんど不要になる。それこそ摩擦力さえなければ、テーブルのちょっとした傾きや、風などの些細な力で動くはずである。
すなわち「水平方向の力」で説明するのではなく、「静止摩擦力が小さくなることで味噌汁は勝手に動く」という説明である。まさに引き算の発想である。
静止摩擦力を振り返ってみると、静止摩擦係数(μ')と地面にかかる力(Mg)の掛け算となっている。この静止摩擦力の算式から、静止摩擦係数 μ' が小さくなるか、地面にかかる力 Mg が小さくなれば、味噌汁は動くはずである。
静止摩擦係数は、上述のとおり筆者は明るくない。「濡れたテーブル」ということで、水があることで一定程度係数が小さくなることは想像できるものの、それだけで動くのであれば味噌汁以外の食器もすべて動くはずである。なので今回はもう片方の「地面にかかる力」に着目し、味噌汁の挙動に迫りたい。おそらく味噌汁の「地面にかかる力」を小さくする『何か』があるはずである。
お椀の質量(味噌汁を含む)をM、お椀の高台の部分の体積をV、気圧をPとすると、お椀は当初Mgの力で地面を押すことになる。そして、水平方向には最大μ'Mgの静止摩擦力が働くこととなる。ここまでは先ほどと同じだ。
しかし、高台に閉じ込められた空気が、熱い味噌汁で温められることによる影響を加味して考えてみると、以下のようになる。
高台の当初の状態(外の空気と同じ状態)を、気圧P1、温度(気温)T1としよう。
この空気が味噌汁に熱されることで、空気の温度がT2(>T1)に熱されたとしよう。高台の体積は変わらないため、ボイル・シャルルの法則により、温度に応じて気圧も高くなり、この時の気圧をP2とすると、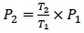 となる。これが単位面積あたりにかかる力となる。
となる。これが単位面積あたりにかかる力となる。
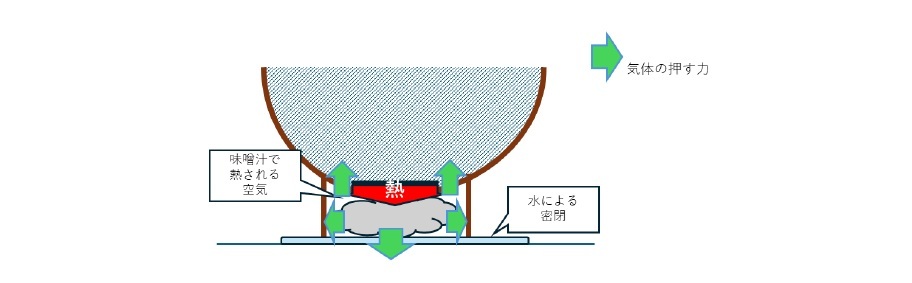
気圧は上下左右に均等に働くため、空気が右に押す力と左に押す力は相殺する。しかし上下に押す力は、お椀と地面が接合していないため、味噌汁と地面を引き離す力として作用する。
お椀(味噌汁を含む)目線で見ると、自重により下向きにMgの力で落下するが、これに空気の力が加わることとなる。自分の上にある空気の力により下向きにP1の力で押され、一方で高台の気圧によって、上向きに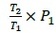 の力で持ち上げられることとなる。気圧は単位面積あたりの力なので、お椀の上面の面積、高台で囲まれた面積を各々乗じたものがお椀にかかる力となる。今回は算式がむやみに煩雑になるのを避けるため(そんなお椀は存在しないが)上面の面積=高台で囲まれた面積=S としたい。すると、気体からの受ける上下の力が相殺し、結果として下方向に
の力で持ち上げられることとなる。気圧は単位面積あたりの力なので、お椀の上面の面積、高台で囲まれた面積を各々乗じたものがお椀にかかる力となる。今回は算式がむやみに煩雑になるのを避けるため(そんなお椀は存在しないが)上面の面積=高台で囲まれた面積=S としたい。すると、気体からの受ける上下の力が相殺し、結果として下方向に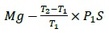 の力が働くことになる。通常、地表での気圧は1cm2あたり約1kgと言われている。温度として用いているT1、T2は日常で用いる摂氏(℃)ではなく、絶対温度(K)である。また、
の力が働くことになる。通常、地表での気圧は1cm2あたり約1kgと言われている。温度として用いているT1、T2は日常で用いる摂氏(℃)ではなく、絶対温度(K)である。また、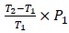 がどの程度の力になるのか、一定程度現実的と思われる数値を当てはめて少し確認してみよう。
がどの程度の力になるのか、一定程度現実的と思われる数値を当てはめて少し確認してみよう。
味噌汁は75℃程度2とすると、高台の空気は味噌汁に触れて、おおざっぱに40℃程度になるとしよう。冬の寒い時期に、室温が10℃とすると、絶対温度では283K(10℃)の空気が323K(40℃)になることになる。これを上式に代入すると、気体による上向きの力は1cm2あたりおよそ100gとなる。これならば、味噌汁を持ち上げることも現実的な水準と言えるのではないだろうか。
1 理想気体の状態方程式PV=nRT(P:気圧、V:体積、n:気体の物質量、R:気体定数、T:温度(K))において、nRが一定とした場合に導かれる。
2 味噌汁は「沸騰させない温度を保つ」というイメージによる
しかし、高台に閉じ込められた空気が、熱い味噌汁で温められることによる影響を加味して考えてみると、以下のようになる。
高台の当初の状態(外の空気と同じ状態)を、気圧P1、温度(気温)T1としよう。
この空気が味噌汁に熱されることで、空気の温度がT2(>T1)に熱されたとしよう。高台の体積は変わらないため、ボイル・シャルルの法則により、温度に応じて気圧も高くなり、この時の気圧をP2とすると、
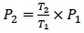 となる。これが単位面積あたりにかかる力となる。
となる。これが単位面積あたりにかかる力となる。気圧は上下左右に均等に働くため、空気が右に押す力と左に押す力は相殺する。しかし上下に押す力は、お椀と地面が接合していないため、味噌汁と地面を引き離す力として作用する。
お椀(味噌汁を含む)目線で見ると、自重により下向きにMgの力で落下するが、これに空気の力が加わることとなる。自分の上にある空気の力により下向きにP1の力で押され、一方で高台の気圧によって、上向きに
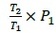 の力で持ち上げられることとなる。気圧は単位面積あたりの力なので、お椀の上面の面積、高台で囲まれた面積を各々乗じたものがお椀にかかる力となる。今回は算式がむやみに煩雑になるのを避けるため(そんなお椀は存在しないが)上面の面積=高台で囲まれた面積=S としたい。すると、気体からの受ける上下の力が相殺し、結果として下方向に
の力で持ち上げられることとなる。気圧は単位面積あたりの力なので、お椀の上面の面積、高台で囲まれた面積を各々乗じたものがお椀にかかる力となる。今回は算式がむやみに煩雑になるのを避けるため(そんなお椀は存在しないが)上面の面積=高台で囲まれた面積=S としたい。すると、気体からの受ける上下の力が相殺し、結果として下方向に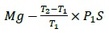 の力が働くことになる。通常、地表での気圧は1cm2あたり約1kgと言われている。温度として用いているT1、T2は日常で用いる摂氏(℃)ではなく、絶対温度(K)である。また、
の力が働くことになる。通常、地表での気圧は1cm2あたり約1kgと言われている。温度として用いているT1、T2は日常で用いる摂氏(℃)ではなく、絶対温度(K)である。また、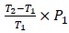 がどの程度の力になるのか、一定程度現実的と思われる数値を当てはめて少し確認してみよう。
がどの程度の力になるのか、一定程度現実的と思われる数値を当てはめて少し確認してみよう。味噌汁は75℃程度2とすると、高台の空気は味噌汁に触れて、おおざっぱに40℃程度になるとしよう。冬の寒い時期に、室温が10℃とすると、絶対温度では283K(10℃)の空気が323K(40℃)になることになる。これを上式に代入すると、気体による上向きの力は1cm2あたりおよそ100gとなる。これならば、味噌汁を持ち上げることも現実的な水準と言えるのではないだろうか。
1 理想気体の状態方程式PV=nRT(P:気圧、V:体積、n:気体の物質量、R:気体定数、T:温度(K))において、nRが一定とした場合に導かれる。
2 味噌汁は「沸騰させない温度を保つ」というイメージによる
2――味噌汁が動くのを防ぐ工夫
味噌汁が動く原理が判明すれば、それを防ぐのはたやすい。
例えば鉛のような重いお椀を用いれば、常識的な温度では気圧で持ち上げられることはないだろう。もっともこの場合「常識的な重さ」から逸脱することになるわけだが。
また、断熱材を使用して高台の空気を温めない方法も考えられる。もしくは、熱した空気を閉じ込めずに循環させる方法もあるだろう。このためには「高台に切れ込みのあるお椀」を用いれば良いのでだいぶ現実的である。
例えば鉛のような重いお椀を用いれば、常識的な温度では気圧で持ち上げられることはないだろう。もっともこの場合「常識的な重さ」から逸脱することになるわけだが。
また、断熱材を使用して高台の空気を温めない方法も考えられる。もしくは、熱した空気を閉じ込めずに循環させる方法もあるだろう。このためには「高台に切れ込みのあるお椀」を用いれば良いのでだいぶ現実的である。
3――その他の要因
上記では、高台内の気体が熱されることのみ注目したが、実際はもう少し他の要因も考えられるだろう。以下では、そのような要素を挙げ、簡単に触れる。
1|テーブルの水の気化
高台とテーブルとの間にある液体の水が、味噌汁の温度によって熱され、一部気化することが考えられる。この気化した水蒸気も、高台内での気体となり味噌汁を上方に押し上げる要因となるだろう。
一般に、気体になると液体よりも体積が大きくなる。その体積を小さい高台内に収めようとすると気体の圧力が上がる。液体のままであれば味噌汁を持ち上げる効果は無いが、このようなプロセスを経て、テーブル上の水も気体となることで味噌汁を持ち上げる効果を発揮することが考えられる。もともと気体であった高台内の空気がボイル・シャルルの法則によって気圧が上がる効果よりも大きい効果を発揮する可能性も考えられる。
高台とテーブルとの間にある液体の水が、味噌汁の温度によって熱され、一部気化することが考えられる。この気化した水蒸気も、高台内での気体となり味噌汁を上方に押し上げる要因となるだろう。
一般に、気体になると液体よりも体積が大きくなる。その体積を小さい高台内に収めようとすると気体の圧力が上がる。液体のままであれば味噌汁を持ち上げる効果は無いが、このようなプロセスを経て、テーブル上の水も気体となることで味噌汁を持ち上げる効果を発揮することが考えられる。もともと気体であった高台内の空気がボイル・シャルルの法則によって気圧が上がる効果よりも大きい効果を発揮する可能性も考えられる。
2|液体の水という潤滑剤
液体の水が高台とテーブルの間に入ることで、静止摩擦係数が小さくなることが考えられる。アイススケートのリンクが滑るのも、氷自体が滑るのではなく、スケートの刃で氷が圧縮されて液体の水となり、その水が滑ると説明されるのが一般的と理解している。水は圧力によって固体(氷)から液体(水)へと状態変化する特殊な物質でもある。
液体の水が高台とテーブルの間に入ることで、静止摩擦係数が小さくなることが考えられる。アイススケートのリンクが滑るのも、氷自体が滑るのではなく、スケートの刃で氷が圧縮されて液体の水となり、その水が滑ると説明されるのが一般的と理解している。水は圧力によって固体(氷)から液体(水)へと状態変化する特殊な物質でもある。
4――まとめ
味噌汁が動くのは、「高台に閉じ込められた気体によって、味噌汁が限りなく浮いている状態にあるため」という示唆を得た。思考実験のみであるため、結論を断言するには更なる検証が必要であると考えられるが、研究員として、また父親として息子に「自然から学ぶ姿勢」を実践する機会となったと考える。『研究員の眼』というレポート趣旨として、今後ともこの姿勢を大切にしたいと思う。
(2025年10月27日「研究員の眼」)

03-3512-1777
経歴
- 【職歴】
2007年 日本生命保険相互会社入社
2024年 ニッセイ基礎研究所
【加入団体等】
・日本アクチュアリー会 正会員
・年金数理人
植竹 康夫のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/27 | なぜ味噌汁は動くのか | 植竹 康夫 | 研究員の眼 |
| 2025/10/24 | 保険業界が注目する“やせ薬”?-GLP-1は死亡率改善効果をもたらすのか | 植竹 康夫 | 研究員の眼 |
| 2025/07/23 | IAISグローバルセミナー開催~資産集約型再保険およびオルタナティブ資産に関するディスカッション~ | 植竹 康夫 | 保険・年金フォーカス |
| 2025/07/01 | 国際的に注目を集めるAsset-Intensive Reinsurance(AIR)を巡る動向 | 植竹 康夫 | 保険・年金フォーカス |
新着記事
-
2025年10月27日
秋の夜長に市民と経済の主食を考える-農業と電力はこれからも日本の食欲を満たせるのか -
2025年10月27日
大学卒女性の働き方別生涯賃金の推計(令和6年調査より)-正社員で2人出産・育休・時短で2億円超 -
2025年10月27日
なぜ味噌汁は動くのか -
2025年10月24日
米連邦政府閉鎖と代替指標の動向-代替指標は労働市場減速とインフレ継続を示唆、FRBは政府統計を欠く中で難しい判断を迫られる -
2025年10月24日
企業年金の改定についての技術的なアドバイス(欧州)-EIOPAから欧州委員会への回答
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【なぜ味噌汁は動くのか】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
なぜ味噌汁は動くのかのレポート Topへ





















 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




