- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 図形数について(その1)-2次元平面図形に関する図形数-
コラム
2022年12月08日
文字サイズ
- 小
- 中
- 大
はじめに
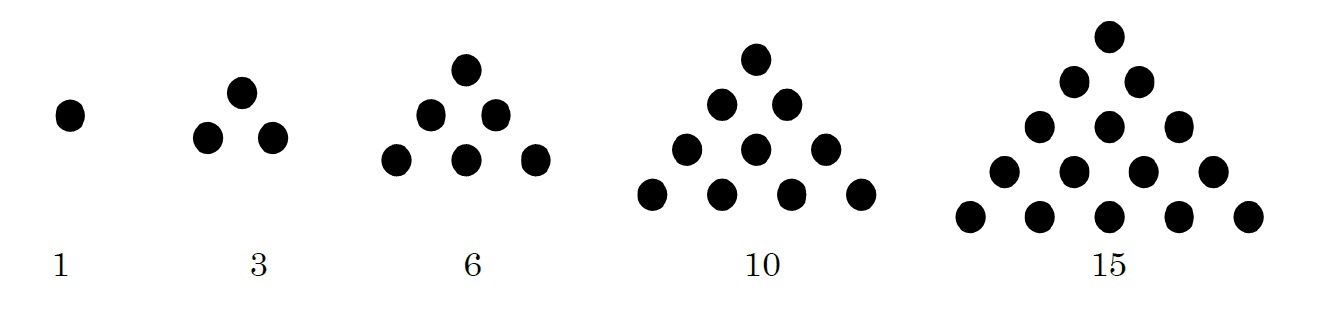
「図形数(figurate number)」と呼ばれるものは、「一定の規則で図形上に並べられた点の個数として表される自然数」を指している。図形数に関する研究の歴史は古く、古代ギリシアのピタゴラス学派は、「万物は数である」、「数学はあらゆるものの基礎である」、「幾何学は数学研究の中で最上位にある」との考え方のもと、図形と結び付けられた数に強い関心を有していたとされている。数字を図形という形で視覚化されたものと結び付ける(むしろ、世の中の形あるものを数字で表してきているといった方が正しいかもしれない)ことで、数字や数学の理解が進んできた面が大きいといえる。
今回は、こうした図形数に関する話題を取り上げることとする。
今回は、こうした図形数に関する話題を取り上げることとする。
三角数の性質
次に、「全ての自然数は、3個以下の三角数で表すことができる。」というものがあり、「ガウスの三角数定理」と呼ばれている。これはパスカルによって主張され、1796年の日記によれば、ガウスによって証明されたと言われている(これに対して、1798年にルジャンドルによって証明されたとも言われている)。この定理の証明は難しいので、興味・関心のある方は専門書にあたってもらいたい。
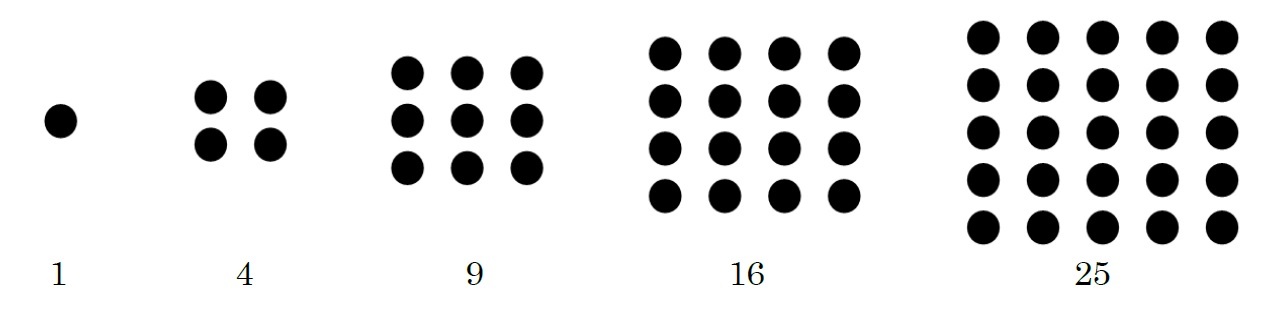
四角数の性質、三角数との関係
さらに、「全ての自然数は、4個以下の四角数(平方数)の和で表される。」(「ラグランジュの四角数定理」あるいは「四平方定理」)というものがある。1772年にフランスの数学者ジョゼフ=ルイ・ラグランジュ(Joseph-Louis Lagrange)によって証明されている。
多角数(五角数、六角数等)
三角数や四角数をより一般化して、任意の自然数nに対して、正n角形の形に点を並べた時に、得られる点の総数を「多角数(polygonal number)」という。
三角数定理や四角数定理は、より一般的な多角数の場合に拡張される、即ち、全てのm≧3 に対して「全ての自然数は m個以下のm角数の和で表すことができる」(「多角数定理(polygonal number theorem)」)。この一般的な定理は、1638年にフェルマーによって定式化され、一般的なケースについては、1813年にフランスの数学者オーギュスタン=ルイ・コーシー(Augustin Louis Cauchy)1によって証明された。
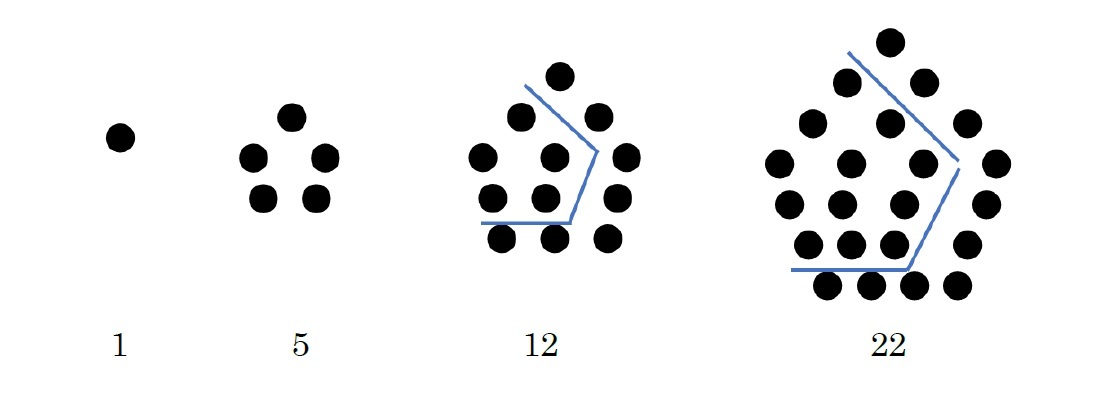
このうちの「五角数」については、以下の通りとなる。
三角数定理や四角数定理は、より一般的な多角数の場合に拡張される、即ち、全てのm≧3 に対して「全ての自然数は m個以下のm角数の和で表すことができる」(「多角数定理(polygonal number theorem)」)。この一般的な定理は、1638年にフェルマーによって定式化され、一般的なケースについては、1813年にフランスの数学者オーギュスタン=ルイ・コーシー(Augustin Louis Cauchy)1によって証明された。
このうちの「五角数」については、以下の通りとなる。
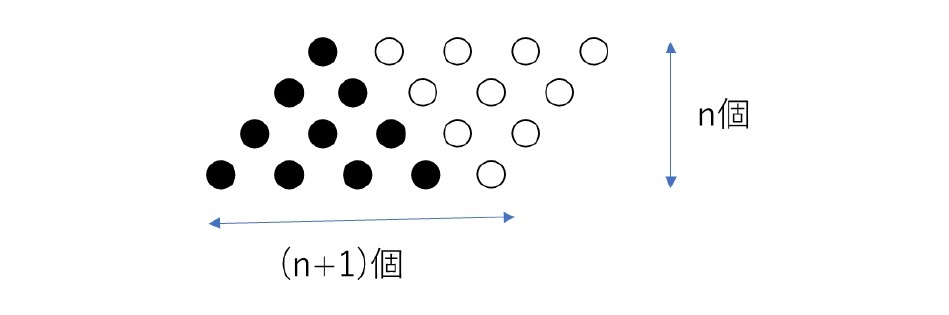
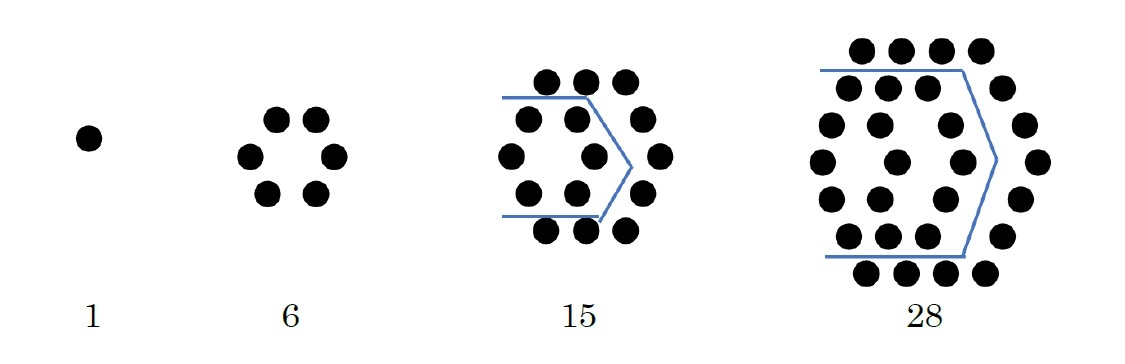
となる。この式から、「n 番目の六角数は (2n-1)番目の三角数に等しい。」即ち、全ての六角数は三角数でもある。
なお、以前の研究員の眼「完全数とその魅力について-「博士の愛した数式」を観て、改めて数字の持つ奥深さに魅せられました-」(2017.2.13)において、「完全数」2について紹介したが、そこで述べたように、これまでに確認された完全数は全て偶数である。偶数の完全数は全て奇数番目の三角数でもあり、「現在知られている完全数は全て六角数」ということになる。
1 学生時代に学んだ数学においても、コーシー分布やコーシー=シュワルツの不等式等にその名が残されており、多大な功績を残している。ラグランジュとともに、エッフェル塔に名前を刻まれた72人のフランスの科学者のうちの一人である。
2 完全数とは、「その数字自身を除く約数の和がその数字自身に等しい自然数」のことをいう。
なお、以前の研究員の眼「完全数とその魅力について-「博士の愛した数式」を観て、改めて数字の持つ奥深さに魅せられました-」(2017.2.13)において、「完全数」2について紹介したが、そこで述べたように、これまでに確認された完全数は全て偶数である。偶数の完全数は全て奇数番目の三角数でもあり、「現在知られている完全数は全て六角数」ということになる。
1 学生時代に学んだ数学においても、コーシー分布やコーシー=シュワルツの不等式等にその名が残されており、多大な功績を残している。ラグランジュとともに、エッフェル塔に名前を刻まれた72人のフランスの科学者のうちの一人である。
2 完全数とは、「その数字自身を除く約数の和がその数字自身に等しい自然数」のことをいう。
三角数でもあり四角数でもある数
ここまで、三角数、四角数、五角数、六角数について紹介してきたが、例えば六角数は全て三角数であると述べた。それでは、三角数でもあり、四角数でもある数は、存在するのだろうか、と疑問に思われる方もいらっしゃるかもしれない。これは実際に存在して、「平方三角数(square triangular number)」と呼ばれている。具体的には「1」以外に、例えば「36」がこれに該当している。36=8×9/2 であり、36=62 でもあることから、36は8番目の三角数であり、6番目の四角数でもある。
これについては、より一般化できる。
ある数がn番目の三角数であり、かつm番目の四角数であるとすると、次の式が成り立つ。
n(n+1)/2 =m2
この式は、以下のように変形できる。
(2n+1)2-2(2m)2 = 1
ここで、x=2n+1、y=2m とおくと
x2-2y2=1
となる。
これについては、より一般化できる。
ある数がn番目の三角数であり、かつm番目の四角数であるとすると、次の式が成り立つ。
n(n+1)/2 =m2
この式は、以下のように変形できる。
(2n+1)2-2(2m)2 = 1
ここで、x=2n+1、y=2m とおくと
x2-2y2=1
となる。
ぺル方程式
一般的に、整数xとyに関する不定方程式 x2-dy2=1 (dは正の整数)は「ぺル方程式(Pell’s equation)」と呼ばれている。
ぺル方程式(に関連した問題)は、大学の入学試験問題にも時々現れてくる。
ぺル方程式において、(x、y)=(1,0)、(-1,0)は自明な解(trivial solution)となる。
ぺル方程式については、以下のことが成り立つ。
(1) ペル方程式には必ず自明でない解が無限個存在する。
(2) ペル方程式の解の中で、x+√d・y を最小にするような解を (x0, y0)とすると、自然数 n を用いてx+√d・y=(x0+√d・y0)n という形で書ける (x,y)もまたペル方程式の解となり、それで全てが尽くされる。
これによれば、先ほどの「平方三角数」に関するペル方程式については、
(3+2√2)n の、整数部をxn、√2の係数をyn とすることで、全ての解が得られることになる。
具体的には、例えば、
(3+2√2)1 = 3+2√2 32-2・22=1 n=1 m=1 数値は1
(3+2√2)2 = 17+12√2 172-2・122=1 n=8 m=6 数値は36
(3+2√2)3 = 99+70√2 992-2・702=1 n=49 m=35 数値は1,225
(3+2√2)4 = 577+408√2 5772-2・4082=1 n=288 m=204 数値は41,616
・・・・・・・
となる。
このように「平方三角数」は無数に存在する。
なお、k番目の平方三角数Nkは、以下の公式で与えられることが、1778年にレオンハルト・オイラー(Leonhard Euler)によって発見されている。
ぺル方程式(に関連した問題)は、大学の入学試験問題にも時々現れてくる。
ぺル方程式において、(x、y)=(1,0)、(-1,0)は自明な解(trivial solution)となる。
ぺル方程式については、以下のことが成り立つ。
(1) ペル方程式には必ず自明でない解が無限個存在する。
(2) ペル方程式の解の中で、x+√d・y を最小にするような解を (x0, y0)とすると、自然数 n を用いてx+√d・y=(x0+√d・y0)n という形で書ける (x,y)もまたペル方程式の解となり、それで全てが尽くされる。
これによれば、先ほどの「平方三角数」に関するペル方程式については、
(3+2√2)n の、整数部をxn、√2の係数をyn とすることで、全ての解が得られることになる。
具体的には、例えば、
(3+2√2)1 = 3+2√2 32-2・22=1 n=1 m=1 数値は1
(3+2√2)2 = 17+12√2 172-2・122=1 n=8 m=6 数値は36
(3+2√2)3 = 99+70√2 992-2・702=1 n=49 m=35 数値は1,225
(3+2√2)4 = 577+408√2 5772-2・4082=1 n=288 m=204 数値は41,616
・・・・・・・
となる。
このように「平方三角数」は無数に存在する。
なお、k番目の平方三角数Nkは、以下の公式で与えられることが、1778年にレオンハルト・オイラー(Leonhard Euler)によって発見されている。
最後に
今回は、図形数のうちの2次元の平面図形に関する数とそれに関連する話題として、ペル方程式について紹介した。
冒頭で述べたように、数字を図形に結び付けることで、イメージが湧きやすくなり、数式の構造の把握等にも役立つことが一定ご理解いただけたのではないかと思っている。
次回は、立方数等の3次元の立体図形に関する数について紹介することにする。
冒頭で述べたように、数字を図形に結び付けることで、イメージが湧きやすくなり、数式の構造の把握等にも役立つことが一定ご理解いただけたのではないかと思っている。
次回は、立方数等の3次元の立体図形に関する数について紹介することにする。
(2022年12月08日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
新着記事
-
2025年10月24日
米連邦政府閉鎖と代替指標の動向-代替指標は労働市場減速とインフレ継続を示唆、FRBは政府統計を欠く中で難しい判断を迫られる -
2025年10月24日
企業年金の改定についての技術的なアドバイス(欧州)-EIOPAから欧州委員会への回答 -
2025年10月24日
消費者物価(全国25年9月)-コアCPI上昇率は拡大したが、先行きは鈍化へ -
2025年10月24日
保険業界が注目する“やせ薬”?-GLP-1は死亡率改善効果をもたらすのか -
2025年10月23日
御社のブランドは澄んでますか?-ブランド透明性が生みだす信頼とサステナビリティ開示のあり方(1)
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【図形数について(その1)-2次元平面図形に関する図形数-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
図形数について(その1)-2次元平面図形に関する図形数-のレポート Topへ




















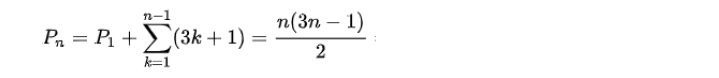
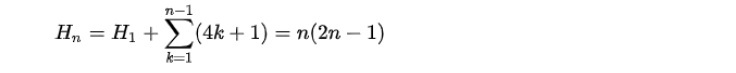
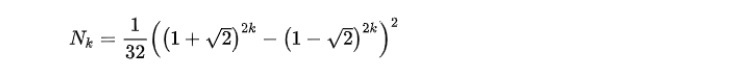

 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




