バークソンのバイアス－合併症の起こりやすさは本当に異なるのか?

保険研究部主席研究員兼気候変動リサーチセンターチーフ気候変動アナリスト兼ヘルスケアリサーチセンター主席研究員篠原拓也

病気の発生動向を研究する学問分野として、疫学がある。ある集団をもとに、病気の発生動向を観測する。そして、得られたデータを統計処理する。その結果、「○○の健康状態の人は、◇◇の病気にかかりやすい」といったことを明らかにする。

昨今のデータサイエンスの隆盛を背景に、疫学の分野では、さまざまな統計解析が進められている。そして、そこで得られた結果をもとに、有効な健康増進策を推進しようという動きも出てきている。

ただし、疫学の統計解析には、一筋縄ではいかない点があるので注意が必要だ。たとえば、病気の合併症について、つぎのような分析をしたとする。

[病気の合併症に関する分析]

(1) 病気Aと病気Cの合併症と、病気Bと病気Cの合併症では、一体どちらが起こりやすいのか？
　　ある病院の診療記録をもとに、割り出すことにしたい。

(2) 病気Aにかかっていた人は620人。そのうち80人は病気Cにもかかっていた。
　　したがって、AとCの合併率は、13% (＝80人÷620人)。

　　一方、病気Bにかかっていた人は240人。そのうち60人は病気Cにもかかっていた。
　　したがって、BとCの合併率は、25% (＝60人÷240人)。

(3) 2つの合併率を比べると、病気Bと病気Cのほうが、病気Aと病気Cよりも高い。
　　そこで、「病気Bと病気Cの合併症のほうが起こりやすい」と結論づけた。

一見すると、この分析には、特段、問題がないようにみえるかもしれない。しかし、実は、大きな問題が潜んでいる。読者のみなさんは、お気付きだろうか？

「ある病院の診療記録」をもとに、合併率を計算していることが問題なのだ。

どんな病気でも、患者がすべて病院に来て診療を受けるわけではない。身体の調子が多少悪くても、しばらく様子をみる人や、市販薬を使って自分で治そう(いわゆるセルフメディケーション)という人がいる。特に、急激な痛みなどを伴わない慢性の病気で、病状が徐々に進行していくような場合には、そうした傾向が強くなるだろう。

つまり、病気にかかってはいるが、病院で受療していない「潜在患者」について、考えてみる必要がある。

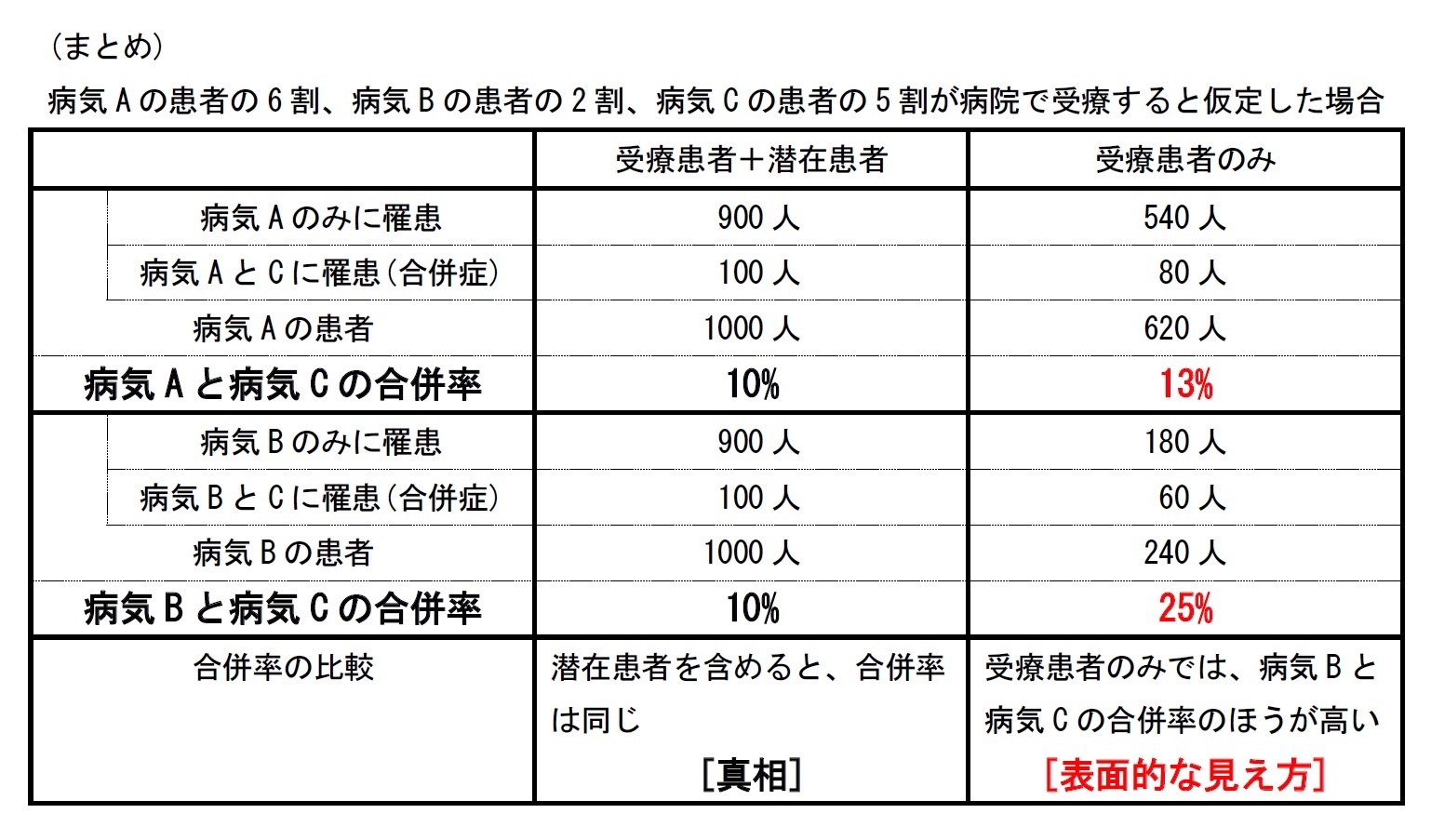
先ほどの例で、「病気Aにかかった患者の6割、病気Bにかかった患者の2割、病気Cにかかった患者の5割が、かかってすぐに病院で受療した」としてみよう。なお、最初から合併症として受療するケースは考慮しないことにする。

このような場合、潜在患者も含めて患者全体でみると、合併率はどうなるだろうか。

まず、病気Aの患者からみてみよう。Aにはかかっているが、Cとの合併症ではない患者は、540人(＝620人－80人)受療していた。これは、患者全体の6割で、背後には、まだ4割の潜在患者がいる。つまりAにはかかっているが、Cとの合併症ではない患者は、潜在患者を含めると、900人(＝540人÷0.6)いることになる。

AとCの合併症の患者はどうか。潜在患者を含めると、全部でX人いるとしよう。そのうちの6割が病気Aで受療し、残りの5割が病気Cで受療する。これを方程式で表すと、

X×0.6 ＋ (X－X×0.6)×0.5 ＝ 80人

となる。この方程式を解くと、X＝100人となる。

つぎに、病気Bの患者をみてみよう。Bにはかかっているが、Cとの合併症ではない患者は、180人(＝240人－60人) 受療していた。これは、患者全体の2割に過ぎず、背後には、さらに8割の潜在患者がいる。つまりBにはかかっているが、Cとの合併症ではない患者は、潜在患者を含めると、900人(＝180人÷0.2)いることになる。

BとCの合併症の患者はどうか。潜在患者を含めると、全部でY人いるとしよう。そのうちの2割が病気Bで受療し、残りの5割が病気Cで受療する。これを方程式で表すと、

Y×0.2 ＋ (Y－Y×0.2)×0.5 ＝ 60人

となる。この方程式を解くと、Y＝100人となる。

まとめると、病気AもBも、それぞれ1000人の患者がいて、病気Cとの合併症の患者が100人ずついる、ということになる。合併率はどちらも10%で、合併症のかかりやすさは同じという結果だ。

(まとめ)病気Aの患者の6割、病気Bの患者の2割、病気Cの患者の5割が病院で受療すると仮定した場合

潜在患者を含めた[真相]は、病気にかかった患者の何割が病院で受療するか、に依存している。この表では、病気Aは6割、病気Bは2割、病気Cは5割としたが、これと別の割合を仮定すれば、計算結果は、また違ったものとなる。

この現象は、アメリカの医師であり統計学者でもあった、ジョセフ・バークソンが1946年に公表したことから、「バークソンのバイアス」と呼ばれている。彼は、糖尿病と胆のう炎の併発の可能性について、病院の記録をもとに行う研究を例に、問題点を指摘した。

現在、ICT(情報通信技術)の高まりを背景に、データ管理やさまざまな統計解析のツールが利用可能となっている。機械的にデータを統計処理して、そこから結論を導くこともできる。しかし、いくら正しい統計処理を行っても、もともとのデータ自体がバイアスに汚染されている可能性がある。

疫学にかかわらず、データサイエンスにもとづく、統計の結果を目にするときには、データの取得にバイアスが絡むなどの問題はないのか、という視点を持つことが必要と思われるが、いかがだろうか。

(参考文献)
「医学統計学シリーズ1　統計学のセンス　デザインする視点・データを見る目」丹後俊郎著 (朝倉書店, 1998年)

日付	タイトル	執筆者	媒体
2025/04/28	リスクアバースの原因－やり直しがきかないとリスクはとれない	篠原拓也	研究員の眼
2025/04/22	審査の差の定量化－審査のブレはどれくらい?	篠原拓也	研究員の眼
2025/04/15	患者数:入院は減少、外来は増加－2023年の「患者調査」にコロナ禍の影響はどうあらわれたか?	篠原拓也	基礎研レター
2025/04/08	センチネル効果の活用－監視されていると行動が改善する?	篠原拓也	研究員の眼

日付

タイトル

執筆者

媒体

2025/04/28

リスクアバースの原因－やり直しがきかないとリスクはとれない

篠原拓也

研究員の眼

2025/04/22

審査の差の定量化－審査のブレはどれくらい?

篠原拓也

研究員の眼