- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 帯分数・仮分数-この呼び方はどこへ行ってしまったのか
コラム
2021年04月27日
文字サイズ
- 小
- 中
- 大
などのように表示したものを帯分数と呼ぶ。そして小学校の算数の時間には、それらを互いに書き直すなどのドリルをさんざんやらされる。(ちなみに「仮分数」は、「過」分数だと今まで筆者は思っていたが、学習指導要領では「仮」となっているから、仕方なく思い違いは認めよう。もう使う機会はないし。)
ところで、小学校の算数では、
「答えが仮分数のままだと×」(何故?)とか
「帯分数は「にかさんぶんのいち」などと読む」(「か」って何?ちなみに筆者の世代は実はすでに「にとさんぶんのいち」など「と」とされていた。)
などと騒いでたのに、中学校では「帯分数」とか「仮分数」とかという用語は、全く聞かなくなってしまったという印象がないだろうか。いったいどうしたことだ?
もちろん、今やその消えた理由すらどうでもいいことではあるが、感想をのべてみたい。
分数を初めて教える時は「みかん1つをいくつかに分けたそのうちいくつ」などという言い方をする。10個にわけた3つ分とかだから、当然1より小さく、それが真の分数である、と。
それが「頭でっかち」な仮分数になると、「みかんひとつを分けただけなのに、それ以上、上に乗ってるのはヘンです!どこから持ってきたんですか?」と言う子もいるのだろう。だからニセモノ?の仮の分数だと思うことにしよう、ということか。それを、「みかん丸々1個と10個に分けた3つ分」」というような「整数+真分数」というホンモノ?にするため、帯分数で表現するのがよいとされたのではないか。
また、数学は、こうすれば計算できるという考え方・手法の方に重きが置かれている。一方、物理では、単位付きの数値によって、大きさの具体的なイメージをもって、答えを出していくことが必要である。その点では、小数が最もわかりやすい表し方であろうが、それに近い帯分数の表示が理科(物理)では重要視されたのではないか。
例えば「100/3」、という表示は、数学としてはもちろん正しいが、日常感覚では、その大きさが「3ではなく30に近い」とイメージすることの方が、正確な答えよりもよっぽど大事なのだ。
数学と物理が徐々に分かれていくのは中学からなので、数学の中では理論が重視されて帯分数でも仮分数でも何でもよくなり、一方物理では、実験結果などを小数で表示することが多くなる。そのため、帯分数は姿を消す? 仮分数も、そのレベルになるともう仮の姿ではないことはわかるだろう。
さらにまた、中学校以上の数学においては文字式が普通に使われ、具体的な数字が比較的少なくなってくる(いや少なくはないのだが)し、掛け算記号が省略されるので、混同をさけるためにも、帯分数は使われなくなるにちがいない。 (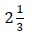 は
は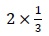 と紛らわしい。)
と紛らわしい。)
一方、分数の掛け算・割り算では、仮分数のまま計算するほうが間違いを避けられそうでもある。
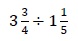 などは、仮分数に直さないとやりようがない。
などは、仮分数に直さないとやりようがない。
ところで、小学校の算数では、
「答えが仮分数のままだと×」(何故?)とか
「帯分数は「にかさんぶんのいち」などと読む」(「か」って何?ちなみに筆者の世代は実はすでに「にとさんぶんのいち」など「と」とされていた。)
などと騒いでたのに、中学校では「帯分数」とか「仮分数」とかという用語は、全く聞かなくなってしまったという印象がないだろうか。いったいどうしたことだ?
もちろん、今やその消えた理由すらどうでもいいことではあるが、感想をのべてみたい。
分数を初めて教える時は「みかん1つをいくつかに分けたそのうちいくつ」などという言い方をする。10個にわけた3つ分とかだから、当然1より小さく、それが真の分数である、と。
それが「頭でっかち」な仮分数になると、「みかんひとつを分けただけなのに、それ以上、上に乗ってるのはヘンです!どこから持ってきたんですか?」と言う子もいるのだろう。だからニセモノ?の仮の分数だと思うことにしよう、ということか。それを、「みかん丸々1個と10個に分けた3つ分」」というような「整数+真分数」というホンモノ?にするため、帯分数で表現するのがよいとされたのではないか。
また、数学は、こうすれば計算できるという考え方・手法の方に重きが置かれている。一方、物理では、単位付きの数値によって、大きさの具体的なイメージをもって、答えを出していくことが必要である。その点では、小数が最もわかりやすい表し方であろうが、それに近い帯分数の表示が理科(物理)では重要視されたのではないか。
例えば「100/3」、という表示は、数学としてはもちろん正しいが、日常感覚では、その大きさが「3ではなく30に近い」とイメージすることの方が、正確な答えよりもよっぽど大事なのだ。
数学と物理が徐々に分かれていくのは中学からなので、数学の中では理論が重視されて帯分数でも仮分数でも何でもよくなり、一方物理では、実験結果などを小数で表示することが多くなる。そのため、帯分数は姿を消す? 仮分数も、そのレベルになるともう仮の姿ではないことはわかるだろう。
さらにまた、中学校以上の数学においては文字式が普通に使われ、具体的な数字が比較的少なくなってくる(いや少なくはないのだが)し、掛け算記号が省略されるので、混同をさけるためにも、帯分数は使われなくなるにちがいない。 (
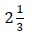 は
は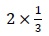 と紛らわしい。)
と紛らわしい。)一方、分数の掛け算・割り算では、仮分数のまま計算するほうが間違いを避けられそうでもある。
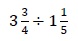 などは、仮分数に直さないとやりようがない。
などは、仮分数に直さないとやりようがない。
(約分せず、帯分数にも直していないと、小学校の算数では、×をくらう可能性大である。)
実際に学習指導要領などにあたってみたが、明確に帯分数や仮分数(という用語の使用)をやめるという段階はない。小学校の学習指導要領の段階で、「大きさの感覚をつかむには帯分数、計算に便利なのは仮分数」という主旨の記載を見かけたので、誰もが自然に便利な方を使っていくのだろう。
中学入試などで「仮分数は帯分数に直して表しなさい」と問題にあったり(そして見落として×となったり)、帯分数どうしの割り算の問題がでて、少し受験生を戸惑わせる。そこまでが最後の晴れ舞台であり、その後は、帯分数・仮分数といった用語や表記をことさら使わなくなっていく、といったところだろうか。
実際に学習指導要領などにあたってみたが、明確に帯分数や仮分数(という用語の使用)をやめるという段階はない。小学校の学習指導要領の段階で、「大きさの感覚をつかむには帯分数、計算に便利なのは仮分数」という主旨の記載を見かけたので、誰もが自然に便利な方を使っていくのだろう。
中学入試などで「仮分数は帯分数に直して表しなさい」と問題にあったり(そして見落として×となったり)、帯分数どうしの割り算の問題がでて、少し受験生を戸惑わせる。そこまでが最後の晴れ舞台であり、その後は、帯分数・仮分数といった用語や表記をことさら使わなくなっていく、といったところだろうか。
本資料記載のデータは各種の情報源から入手・加工したものであり、その正確性と完全性を保証するものではありません。
また、本資料は情報提供が目的であり、記載の意見や予測は、いかなる契約の締結や解約を勧誘するものではありません。
(2021年04月27日「研究員の眼」)

03-3512-1833
経歴
- 【職歴】
1987年 日本生命保険相互会社入社
・主計部、財務企画部、調査部、ニッセイ同和損害保険(現 あいおいニッセイ同和損害保険)(2007年‐2010年)を経て
2012年 ニッセイ基礎研究所
【加入団体等】
・日本アクチュアリー会 正会員
・日本証券アナリスト協会 検定会員
安井 義浩のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/31 | 保険型投資商品の特徴を理解すること(欧州)-欧州保険協会の解説文書 | 安井 義浩 | 保険・年金フォーカス |
| 2025/10/24 | 企業年金の改定についての技術的なアドバイス(欧州)-EIOPAから欧州委員会への回答 | 安井 義浩 | 保険・年金フォーカス |
| 2025/10/17 | EUの金融システムのリスクと脆弱性(2025秋)-欧州の3つの金融監督当局の合同委員会報告書 | 安井 義浩 | 基礎研レター |
| 2025/10/10 | 保険・年金関係の税制改正要望(2026)の動き-関係する業界・省庁の改正要望事項など | 安井 義浩 | 基礎研レター |
新着記事
-
2025年11月04日
今週のレポート・コラムまとめ【10/28-10/31発行分】 -
2025年10月31日
交流を広げるだけでは届かない-関係人口・二地域居住に求められる「心の安全・安心」と今後の道筋 -
2025年10月31日
ECB政策理事会-3会合連続となる全会一致の据え置き決定 -
2025年10月31日
2025年7-9月期の実質GDP~前期比▲0.7%(年率▲2.7%)を予測~ -
2025年10月31日
保険型投資商品の特徴を理解すること(欧州)-欧州保険協会の解説文書
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【帯分数・仮分数-この呼び方はどこへ行ってしまったのか】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
帯分数・仮分数-この呼び方はどこへ行ってしまったのかのレポート Topへ

















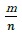 (ここではn、mは整数としておく。)の形の数である。1/2 、3/5、 7/3 などである。
(ここではn、mは整数としておく。)の形の数である。1/2 、3/5、 7/3 などである。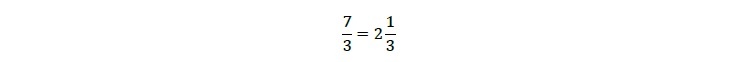
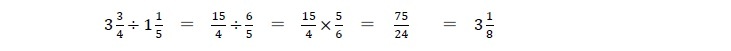

 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




