- シンクタンクならニッセイ基礎研究所 >
- 経済 >
- 経済予測・経済見通し >
- 回帰分析を理解しよう!-回帰分析の由来と概念、そして分析結果の評価について-
文字サイズ
- 小
- 中
- 大
1――回帰分析の由来
回帰分析が世の中に登場するまでには少なくとも4人の学者の貢献があった。まず、フランスの数学者ルジャンドル(Adrien-Marie Legendre 、1752~1833)は、回帰分析の代表的な手法である「最小二乗法」のアイディアを最初(1805年)に発表した1。最小二乗法(OLS,Ordinary Least Squares)とは、残差(観測値と予測値の差)の二乗和を最小にする推計方法である(詳細は次の節で説明)。その後、最小二乗法を発展させたのがドイツの数学者(天文学者で物理学者でもある)であるガウス(Carl Friedrich Gauss、1777-1855)である。ガウスは、惑星の軌道を予測する計算方法として最小二乗法を用いた。それから、イギリスの遺伝学者であるゴルトン(Francis Galton、1822-1911)は、親と子どもの身長を分析し、非正常的に身長が大きい子どもと小さい子どもの身長は全人口の平均身長に回帰する傾向があることを見つけた。ゴルトンはこの現象を平均からの回帰(regression to the mean)と呼び、回帰という言葉が始めて分析の中で使われるようになった。また、ゴルトンの友人であるピアソン(Karl Pearson, 1857-1936)は1,000人以上のデータを集めて、身長が高いお父さんグループの子どもの平均身長はお父さんより小さく、身長が低いお父さんグループの子どもの平均身長はお父さんより大きいという「普遍的回帰の法則(law of universal regression)」を証明した。この結果は親の身長がいくら高くても子どもの身長は子どもの世帯の平均の近接する傾向があることを意味している。
1 ガウスは、最小二乗法の原理を1794年に初めて発見したと主張しており、ルジャンドルとの間に最小二乗法の発見をめぐって論争が続いたそうだ。
2――回帰分析の概念
式1)は、教育年数と賃金の多寡の関係をみた単回帰分析の方程式である。教育年数は影響を与える説明変数(X)、賃金は影響を受ける被説明変数(Y)と置くこととする。そして、
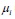 は誤差項で、賃金の変化のうち教育年数で説明できない部分、つまり教育年数以外に賃金に影響を与える要因の合計である。
は誤差項で、賃金の変化のうち教育年数で説明できない部分、つまり教育年数以外に賃金に影響を与える要因の合計である。
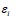 が固定されている場合、教育年数1年の変化は賃金をβだけ変化させることになる。
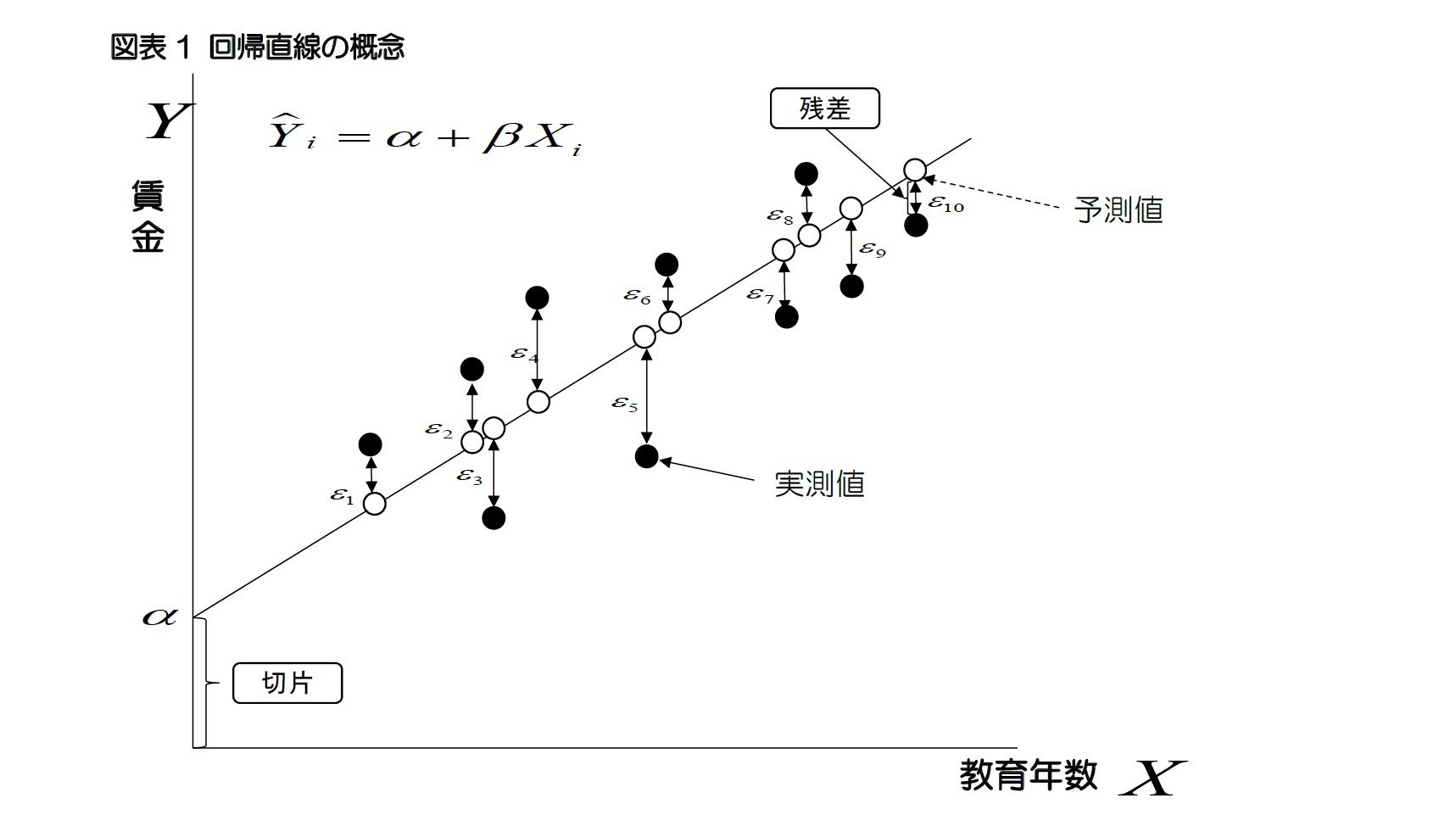
が固定されている場合、教育年数1年の変化は賃金をβだけ変化させることになる。式1)の方程式の目標は見えないパラメータ(parameter)であるαとβを推計することであり、より正確なパラメータを推計する方法として使われているのが最小二乗法である。最小二乗法は、観測値と予測値の差である「残差(residuals)2」の二乗和が最小になるようにαとβを推計する方法である。例えば、図表1の黒丸(●)は実際に測定された実測値であり、その中に描かれている近似線は実測値との残差を最も小さくするために推計された予測値である白丸(○)を繋げた近似線、つまり回帰直線である。一方、被説明変数の予測値は、
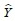 のように書けるので、式1)の予測式は式2)のようになる。
のように書けるので、式1)の予測式は式2)のようになる。
3――分析結果の判断
まず、分析の結果から確認できるのがR2で表示される決定係数(coefficient of determination)であり、これは説明変数が被説明変数をどれくらい説明できるかを表す。決定係数は0から1の範囲内の値を取り、決定係数が1に近いほど説明力が高いことを意味する。しかしながら、社会科学関連の分析では決定係数が低い場合が頻繁にある。その理由としては被説明変数に影響を与えると思われるすべての変数が利用できないことや、分析者が選択した一部の変数のみが説明変数として利用されている点などが挙げられる。そして、線形モデルの場合、決定係数は相関係数の二乗に等しいので、例えば、決定係数が0.2だとしても、これを相関係数に直すと0.45に当たるので決して低い数値だとは言えず、ある程度は説明力があると解釈できる。
次に分析結果が統計的に意味のある分析かどうかを確認するために使うのか有意確率と有意水準である。分析の前には、仮説が正しいかどうかの判断のために帰無仮説を立てるのが一般的である。帰無仮説は、例えば「Aという説明変数は被説明変数に何の影響も与えていない」あるいは「AとBの平均には差がない」のように、たいていは否定されることを期待して立てられる。一方、検定しようとする帰無仮説に対立する仮説が対立仮説であり、これは帰無仮説を棄却するために使われる。帰無仮説と対立仮説を式として表すと式8)と式9)の通りである。
そして、有意確率とともに確認すべきことがtである。tは、係数の値を係数の標準誤差6で除したものであり、説明変数が被説明変数に与える影響の大きさを表す。絶対値が大きければ大きいほど影響が強く、一般的にはtが2以上7なら、その説明変数が被説明変数を十分に説明していると判断される。面白いことは、tは上記で説明したPとは逆の関係にあることである。つまり、tが大きいとPは小さく、逆にtが小さいとPは大きいという結果になる。
4 松村 明 (編集)『大辞林第三版』(2006)では、有意水準を「帰無仮説が真のときに統計量が棄却域に入る確率」と説明している。
5 状況によっては10%が使われる場合もある。
6 標準誤差が小さいほどtが大きくなり、説明力が高まる。
7 厳密には、pが0.1の時にtはおよそ1.68になるので、tが1.68より大きければ、説明変数が被説明変数を説明していると判断できる(ぎりぎりセーフ)。
4――結びに代えて
(2018年05月16日「基礎研レター」)
このレポートの関連カテゴリ

生活研究部 上席研究員・ヘルスケアリサーチセンター・ジェロントロジー推進室兼任
金 明中 (きむ みょんじゅん)
研究・専門分野
高齢者雇用、不安定労働、働き方改革、貧困・格差、日韓社会政策比較、日韓経済比較、人的資源管理、基礎統計
03-3512-1825
- プロフィール
【職歴】
独立行政法人労働政策研究・研修機構アシスタント・フェロー、日本経済研究センター研究員を経て、2008年9月ニッセイ基礎研究所へ、2023年7月から現職
・2011年~ 日本女子大学非常勤講師
・2015年~ 日本女子大学現代女性キャリア研究所特任研究員
・2021年~ 横浜市立大学非常勤講師
・2021年~ 専修大学非常勤講師
・2021年~ 日本大学非常勤講師
・2022年~ 亜細亜大学都市創造学部特任准教授
・2022年~ 慶應義塾大学非常勤講師
・2019年 労働政策研究会議準備委員会準備委員
東アジア経済経営学会理事
・2021年 第36回韓日経済経営国際学術大会準備委員会準備委員
【加入団体等】
・日本経済学会
・日本労務学会
・社会政策学会
・日本労使関係研究協会
・東アジア経済経営学会
・現代韓国朝鮮学会
・博士(慶應義塾大学、商学)
金 明中のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/07/08 | 「静かな退職」と「カタツムリ女子」の台頭-ハッスルカルチャーからの脱却と新しい働き方のかたち | 金 明中 | 基礎研マンスリー |
| 2025/06/06 | “サヨナラ”もプロに任せる時代-急増する退職代行サービス利用の背景とは? | 金 明中 | 基礎研マンスリー |
| 2025/06/02 | 日韓カップルの増加は少子化に歯止めをかけるか? | 金 明中 | 研究員の眼 |
| 2025/05/22 | 【アジア・新興国】韓国の生命保険市場の現状-2023年のデータを中心に- | 金 明中 | 保険・年金フォーカス |
新着記事
-
2025年11月04日
数字の「26」に関わる各種の話題-26という数字で思い浮かべる例は少ないと思われるが- -
2025年11月04日
ユーロ圏消費者物価(25年10月)-2%目標に沿った推移が継続 -
2025年11月04日
米国個人年金販売額は2025年上半期も過去最高記録を更新-但し保有残高純増は別の課題- -
2025年11月04日
パワーカップル世帯の動向(2)家庭と働き方~DINKS・子育て・ポスト子育て、制度と夫婦協働が支える -
2025年11月04日
「ブルー寄付」という選択肢-個人の寄付が果たす、資金流入の突破口
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【回帰分析を理解しよう!-回帰分析の由来と概念、そして分析結果の評価について-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
回帰分析を理解しよう!-回帰分析の由来と概念、そして分析結果の評価について-のレポート Topへ

















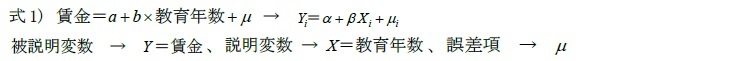


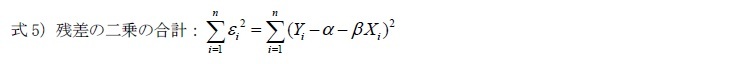
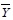 からXの平均
からXの平均




 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




