- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 人間の直感の不確実性-数学的な正しさと乖離している場合があることを知っていますか
2016年11月09日
文字サイズ
- 小
- 中
- 大
1―はじめに
人間の直感が非常に役に立つことは理解されるが、時として、この直感が数学的には正しくないことがあることは有名な話である。
2――誕生日のパラドックス
となる。n=23の場合に、この数値は0.507となって50%を超える。
同じ考え方により、41人の人がいれば、90%以上の確率で、70人の人がいれば、99.9%以上の確率で、誕生日が同じ人がいることになる。これは、直感的には驚くべきことのように思われるのではないか。
これが「パラドックス」と呼ばれるのは、論理的な矛盾がある、という意味ではなく、あくまでも、一般的な直感に反している、という意味で、このように称されている。
一方で、この数値を100%にするには、当然のことながら、366人(うるう年も考慮すれば、367人)必要ということになる。このように、100%を追求することは極めて難しい、わずか0.1%のために5倍以上の人が必要になってくる。
同じ考え方により、41人の人がいれば、90%以上の確率で、70人の人がいれば、99.9%以上の確率で、誕生日が同じ人がいることになる。これは、直感的には驚くべきことのように思われるのではないか。
これが「パラドックス」と呼ばれるのは、論理的な矛盾がある、という意味ではなく、あくまでも、一般的な直感に反している、という意味で、このように称されている。
一方で、この数値を100%にするには、当然のことながら、366人(うるう年も考慮すれば、367人)必要ということになる。このように、100%を追求することは極めて難しい、わずか0.1%のために5倍以上の人が必要になってくる。
3――誕生日問題
となる。23人の場合にはわずか6%であり、50%を超えるためには、253人いなければならなくなる。さらに、99%以上の確率となるためには、1,679人、99.9%以上の確率となるためには2,518人いなければならない。
この誕生日のパラドックスは情報科学において様々に応用されており、代表的なものでは、ハッシュテーブルというデータ構造におけるテーブルの大きさを決めるのに利用されている。
この誕生日のパラドックスは情報科学において様々に応用されており、代表的なものでは、ハッシュテーブルというデータ構造におけるテーブルの大きさを決めるのに利用されている。
4――具体例
5――直感力を養うことの重要性
このように、人間の直感は、結構当てにならないことがわかる。
物事を進めていく上で、過去の経験等に基づいた直感を働かせることはもちろん重要なことであるが、時として、その直感が誤ったものとなっていることがある。
こうした直感は、経験を積むことで、感度を高め、磨きをかけていくことが可能だと思われる。その意味では、いろいろなケースを学ぶことを通じて、知識を充実させていくことが、いざという時に役立つ、適切な直感力を発揮する上でも、重要なことであると、改めて感じさせられる。
物事を進めていく上で、過去の経験等に基づいた直感を働かせることはもちろん重要なことであるが、時として、その直感が誤ったものとなっていることがある。
こうした直感は、経験を積むことで、感度を高め、磨きをかけていくことが可能だと思われる。その意味では、いろいろなケースを学ぶことを通じて、知識を充実させていくことが、いざという時に役立つ、適切な直感力を発揮する上でも、重要なことであると、改めて感じさせられる。
(2016年11月09日「基礎研マンスリー」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/11/04 | 数字の「26」に関わる各種の話題-26という数字で思い浮かべる例は少ないと思われるが- | 中村 亮一 | 研究員の眼 |
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
新着記事
-
2025年11月07日
フィリピンGDP(25年7-9月期)~民間消費の鈍化で4.0%成長に減速、電子部品輸出は堅調 -
2025年11月07日
次回の利上げは一体いつか?~日銀金融政策を巡る材料点検 -
2025年11月07日
個人年金の改定についての技術的なアドバイス(欧州)-EIOPAから欧州委員会への回答 -
2025年11月07日
中国の貿易統計(25年10月)~輸出、輸入とも悪化。対米輸出は減少が続く -
2025年11月07日
英国金融政策(11月MPC公表)-2会合連続の据え置きで利下げペースは鈍化
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【人間の直感の不確実性-数学的な正しさと乖離している場合があることを知っていますか】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
人間の直感の不確実性-数学的な正しさと乖離している場合があることを知っていますかのレポート Topへ



















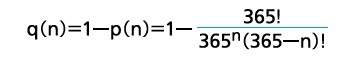
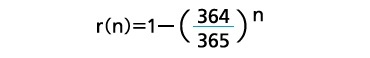


 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




