ベスト・ベターな秘書をどうやって選んだらよいのか－「秘書問題」で効率的な選択を実現する

はじめに

いくつかの選択肢がある場合に最適の選択を行うには、どのような基準に基づいて行えばよいのかという問題は、常に悩ましい問題である。いくつかの条件が複雑に絡み合って、物事は単純には解決しない。ただし、数学の世界では、一定の条件の下での、最良選択をどのように行うべきかの研究が行われており、簡単な例ではシンプルな結論も得られている。

このレポートでは、一般的に「秘書問題」と呼ばれるものを紹介する。これは、しばしば「結婚問題」や「最良選択問題」等幅広くいろいろな呼び方をされているものである。最初のいくつかの選択肢を見送った後、それらの選択肢との比較に基づく一定の基準に従って、最終的な選択を行うという典型的な「最適停止問題」のケースとなっている。

秘書問題－最良選択問題－

秘書問題とは、具体的には以下のような問題である。

前提条件
１．秘書を1人採用することを考える。
２．ｎ人が応募してくるものとする。ｎは既知とする。
３．ｎ人の応募者と無作為に1人ずつ面接を行う。
４．応募者に面接後、その応募者の採用の是非を即座に決定する。
５．不採用にした応募者を後から採用することはできない。
６．応募者は採用を決して断らない。
７．応募者には順位が付けられ、複数の応募者が同じ順位になることはない。

こうした前提条件下で、「最良の応募者を採用する確率を最大にする」にはどうしたらよいのか。

結論から言うと、この問題に対する最適戦略は、

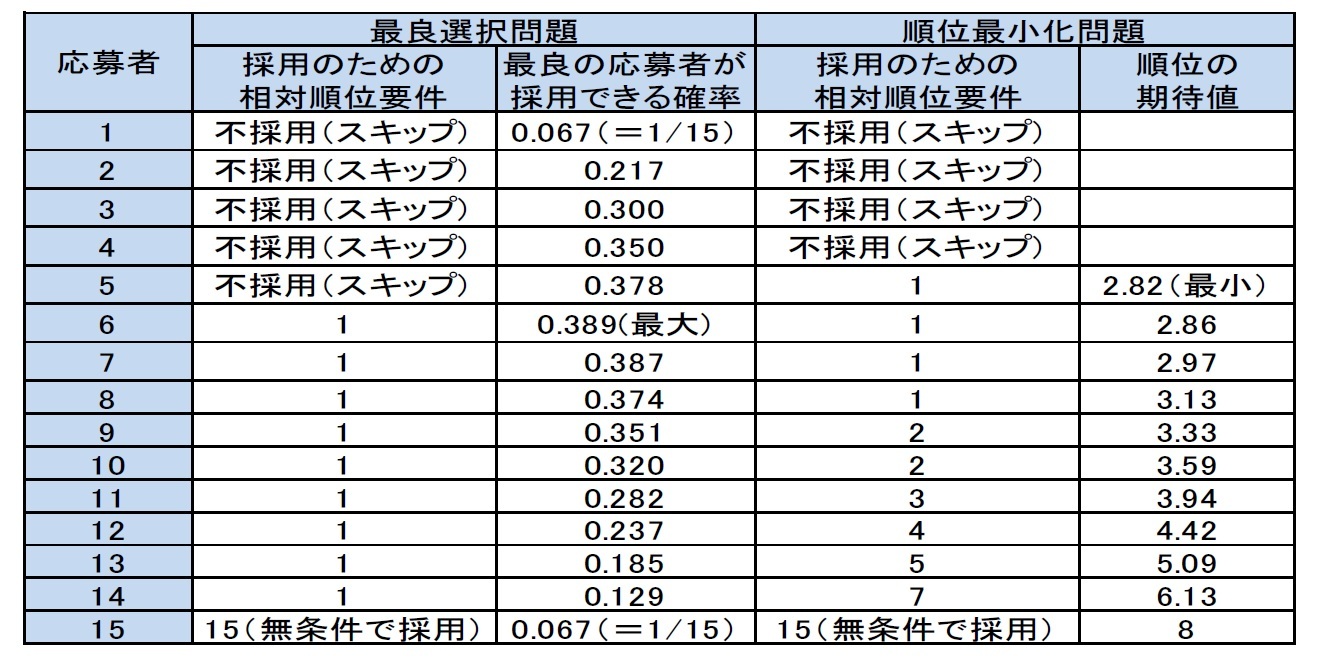
ということになる。この時、最良の応募者を採用できる確率は１／e、即ち約37％となる。これにより、この最適戦略については、「37％の法則」とか「37％ルール」と呼ばれることもある。

秘書問題のバリエーション－順位最小化問題－

秘書問題は、あくまでも「最良の応募者を採用する確率を最大にする」にはどうしたらよいかを考えている。一方で、最良ではなくてもよいから、「よりよい応募者を採用する確率を最大にする」という問題を考えることができる。

即ち、順位の期待値を最小化（逆に言えば、応募者の順位付けに応じた価値を付す場合は、その期待値を最大化）することが考えられる。これを「順位最小化問題」と称している。

この場合の結論は、より難しくなる。

「数学100の問題－数学史を彩る発見と挑戦のドラマ－」（日本評論社）によれば、以下の通りとなる（秘書問題に合わせる形に表現を修正）。

さらに、「秘書問題－２つの最適停止問題の不思議な対応－」（玉置光司）によれば、この場合の最適戦略については、以下の通りとなる。

このように、「順位最小化問題」の場合には、「最良選択問題」の場合と比べて、スキップする人数がより少なくなる。一般的な感覚としては、この最適戦略の方がより実感に合っているかもしれない。

なお、順位の期待値の最小値は、応募者数ｎが大きくなると大きくなっていくが、それでも3.87という値に近づいていくことが証明されている。即ち、上記の戦略に従えば、ｎがどんなに大きくても平均的には4位以下の人を選ぶことができる、ということになる。

具体例

ｎ＝15の場合の具体数値を、上に述べた算式に基づいて計算してみると、以下の通りとなる。

秘書問題の実際

以上、シンプルなケースにおける理論的にあるべき最適戦略について、述べてきた。

ただし、実際の選択の場面では、人は早めに決定を行う傾向がある。例えば、秘書問題の最適戦略を採った場合において、最初のｎ／e人の中に最良の応募者が含まれていた場合には、結局は最後の応募者を選択することになる。その場合には、その応募者の順位の期待値は、全体の平均ということになってしまう。従って、一般的には、一定程度満足感が得られるのであれば、最適でなくてもそれを選択する傾向が強いことになる。不採用を決断して、その後の応募者に満足できなかった場合には、以前の応募者を失ったことに伴う損失感が大きくなりがちだからである。

さらに、現実に当てはめてみた場合、実際には、ここで述べた秘書問題における前提は、必ずしも十分に満たされるわけではない。

特に、「６．応募者は採用を決して断わらない。」との前提は、よほど採用者側に絶対的な優位性がない限り、かなり難しい前提になっている。特に、これを「結婚問題」に当てはめる場合には、自分に絶対的な選択権がある人は、そうはいないことから、必ずしも適切な前提とはいえず、あくまでも参考として考えるしかない。

一方で、「５．不採用にした応募者を後から採用することはできない。」も必ずしも当てはまらないかもしれない。現実には、複数段階の選択で、採用する側と採用される側の意思の相互確認が行われていくプロセスが、多くのケースで利用されているものと思われる。

ここで、紹介したものは、あくまでも基本的でシンプルなケースに相当するものである。例えば、応募者に拒否権があるケースや複数の応募者が選択されるケース等のより複雑な前提下での最適戦略の研究も行われている。

いずれにしても、こうした理論上の最適戦略が現実にどの程度適合するのかという問題は別にして、こうした理論の存在を一定程度認識した上で、事に臨むことも重要なことであると考えられる。

(参考) 秘書問題―最適選択問題

一応、数学的に自ら検証してみないと気がすまないという方々のために、この問題を算式で示しておくと、以下の通りとなる。

このP（ｒ）の最大値については、ｎが大きくなるにつれて減少する。そして、「ｎが無限大に近づくと　１／eに収束する。」ことが証明されているが、これについては、ここでは詳しくは触れない。

ベスト・ベターな秘書をどうやって選んだらよいのか－「秘書問題」で効率的な選択を実現する－ | ニッセイ基礎研究所

ベスト・ベターな秘書をどうやって選んだらよいのか－「秘書問題」で効率的な選択を実現する－