- シンクタンクならニッセイ基礎研究所 >
- 経済 >
- 経済予測・経済見通し >
- 今、経済学に期待されること - 数式に変換された経済モデルの可能性と限界
今、経済学の分野では年間約2万本(凡そ、経済学:13千本、金融:3千本、ビジネス:5千本)もの論文が生まれているのをご存知だろうか。2007年7月に表面化したサブプライム問題、2008年のリーマンショック、そして今日に至るまで続く欧州危機など、世界経済をいっそう不安定な状態へ追いやることが続けて起こっている。さらに、世界人口の増加や環境問題、争い、貧困また天災そして人々のマインドや消費行動といった諸々の不確実要素は、世界の経済メカニズムと無関係ではない。この仕組みを少しでも解きほぐし、世界を発展させようと、ミクロ、マクロなど、様々な角度から研究されている。しかし、混沌(カオス)といっていいほど複雑な世界経済のメカニズムを分析することを目指すがゆえに、経済学は有効な政策を打ち出せず、事象の後追いとなることも少なくない。そのため、経済、金融モデルを揶揄するたくさんのジョークが生まれ、経済学者自身も話の掴みに自虐することもあると聞く。例えば、2012年10月26日の日本経済新聞でも取り上げられた次のようなジョークがある。
【ジョーク1:無人島にて】
船が難破し、無人島に物理学者、化学者、経済学者が漂着した。
そこに、浜辺に船から流れ着いた缶詰があるのを発見したが、しかし、缶切りがない。
物理学者が言った。「石をぶつけてあけよう」。これ対して化学者は、「たき火をして熱で破裂させてはどうか」と提案した。2人は経済学者にも意見を求めた。「どうすればいいと思う?」経済学者が答えた。「よし、ここに缶切りがあると仮定しよう・・・」
多岐にわたる分野を擁する経済学を一緒くたに言及することはできないが、モデルとは現実の捨象であり、その重要性は適切な仮定を置きできるだけ単純な形で本質的なものを描いてみせることである。上記のジョークは、缶切りがないなかで如何に缶詰を開けるか?が問題であり、缶切りがあることを仮定した時点で、問題の本質を見失っている。これは少し極端なジョークであったとしても、経済モデルがこのように揶揄されるわけと経済学者自身さえ自虐する理由をもう少し考える必要はあるだろう。単純化のプロセスは、問題を整理した上で真に理解し、本質を捉えてなくては行えないものである。どこまで複雑な事象を考察対象にしたかにもよるが、ノーベル経済学賞1を受賞するほどの研究者が作ったモデルであれば、このプロセスは少なからず、クリアしていることだろう2。しかし問題は、これに止まらない。仮にそうしたモデルを目の前にしたとしても、モデルを機能させるためには、正しい情報をモデルに入力することが必要で、残念なことに入力する情報がすべて確かなものでないことにある。そのためか、こんなジョークもある。
【ジョーク23:経済学者のささやき】
数学者と会計士、そして経済学者が面接試験を受けに来た。面接官が「2+2はいくつか?」と数学者に質問すると「4だ」と答えた。「本当ですか?」と聞き返すと「当然ですよ、確実に4です」と激高した。同じ質問に会計士は「平均的に4でしょう」と言った。経済学者にもこの質問をすると、徐に立ち上がり、ドアの鍵を閉め、面接官の隣に座り、「どの数字と等しいといってほしいのかい?」とささやいた。
このジョークは、経済学者が真理の追究を怠り、単なる御用学者であることを揶揄している。しかしその根底には、三者が取り扱う入力情報の不確かさ4に違いがあるのではないだろうか。つまり、経済学が取り扱う入力情報には過分の不確実性が伴う。数学者であれば「確実に」、会計士であれば「平均的に」結果をはじきだす。一方、経済学者であれば、尤もらしい理由をつけて入力値の設定を行うことができ、そして、結果を自在に変えてしまえるというわけだ。この場合であれば、経済モデルは本質(ここでは“足算演算”)を捉えているわけであるから、これをもって経済モデルを完全に否定することはできない。
具体的にこの問題について考察するため、金融経済学に焦点をあて、実際にノーベル経済学を受賞したモデルを1つ見てみよう。下図のモデル5は金融派生商品(オプション価格)の価格付け公式である。この経済モデルは、本質を捉えていることもあり、1973年4月に開設されたシカゴオプション取引所が今や15兆ドルを超える規模になった立役者とも言われている。しかし、この一流のモデルであっても、不確かな入力値(株価の変動幅の比率)があり、その結果、この入力を大幅に誤れば、出力値のオプション価格は信用できない。
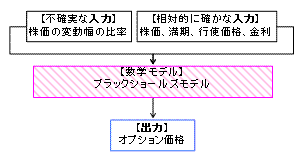
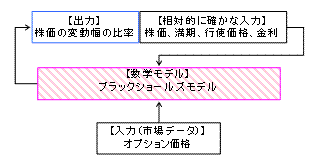
これに関する解決策はなかなか難しいものの、実務での活用をみていると、やはりモデルの構築に意味があるといえる。例えば、市場が成熟し、大規模な売買が日々成立するようになった昨今、何もオプション価格を導出する必要はなく、価格は市場で観測できる。つまり、算出したかった出力値が相対的に確かな値に変わったのである。これにより、これまでの出力値を(入力値として)モデルに入力すれば、不確実な入力値が逆に(出力値として)出力される。この考えに基づき出力された値6は、逆算された株価変動幅の比率(インプライドボラティリティ)といわれ、実務の現場で多く出くわすことがある。
過去のデータや定性的な判断から、株価変動幅の比率を推計しなくても、市場のデータに基づき、値を算出できるというわけだ(下図)。プロの投資家やリスク管理担当者でなければ、複雑な金融派生商品価格(オプション価格)より、むしろ市場のメインプレーヤーが決定する身近な株価の変動に興味があるのではないだろうか。
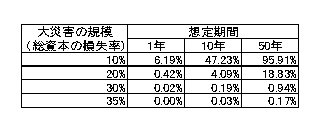
こうした形での試み(成果)は金融経済学の分野に限らずみられる。例えば、一般均衡の分野でもPindyckの経済モデル7は、現在観測できる経済指標の入力で、予測できない大災害の発生確率や規模を逆算してみせた8。これまでの経験則や地球物理学的な見解から想定されるシナリオを推測することも当然重要である。しかし、世界経済メカニズムをできるだけ単純な形でその本質を描ききり(モデル化し)、更に入力値も観測できる確かなものにしようとする経済学者の試みと経済モデルの可能性に、心を躍らせる人も少なくないと思う。
とはいえ、ジョークの対象となってしまうように、昨今の経済理論は、経済の概念を数式に変換するための研究を主にして発展してきたことも確かである。高度な数学や統計も科学的アプローチとしては、必須である。しかし、常に数式という枠をあてがっていては、現実的な価値を持つ“独創的で革新的かつ有益なアイデアの考案”は限定的なものになるのではないだろうか。経済学的側面と政治的側面を混合していると言われるかもしれない。しかし、資源の枯渇、環境問題、産業構造の変化に対応しきれない労働の流動化といった様々な問題が顕在化し、“成長”を前提とした資本主義経済は限界に達している。資本主義経済の進化系なのか、全く新しい形態なのかはわからないが、人類の50年、100年、1000年先を見据えた“経済パラダイムの変革”が期待されていることは間違いない。経済学者に対する尊敬の念をこめて願うことは、経済学者及び経済モデルへの取るに足りないジョークなど一蹴し、経済学者は大局に立ち、様々な角度から人類の展望を望ましい形でぜひ描ききってもらいたいということだ。
このレポートの関連カテゴリ
大山 篤之
研究・専門分野
公式SNSアカウント
新着レポートを随時お届け!日々の情報収集にぜひご活用ください。
新着記事
-
2024年04月30日
今週のレポート・コラムまとめ【4/23-4/26発行分】 -
2024年04月26日
ドイツの産業空洞化リスク-グローバル化逆回転はドイツへの逆風、日本への追い風か?- -
2024年04月26日
米GDP(24年1-3月期)-前期比年率+1.6%と前期から低下、市場予想の+2.5%も大幅に下回る -
2024年04月26日
滞留するふるさと納税 -
2024年04月26日
EUのDMA関連調査開始決定-GAFAそれぞれの問題を指摘
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2024年04月02日
News Release
-
2024年02月19日
News Release
-
2023年07月03日
News Release
【今、経済学に期待されること - 数式に変換された経済モデルの可能性と限界】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
今、経済学に期待されること - 数式に変換された経済モデルの可能性と限界のレポート Topへ



















 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!





