- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 数字の「17」は結構興味深い数字だって知っていますか
コラム
2022年05月20日
文字サイズ
- 小
- 中
- 大
はじめに
数字の「17」と聞くと、多くの人は何か中途半端(?)な数字だなと感じられるのではないだろうか。それでも、世の中には結構「17」と言う数字が興味深い形で現れてくる。
今回は、この数字の「17」に関する各種の話題について、まとめてみた。
今回は、この数字の「17」に関する各種の話題について、まとめてみた。
数字の「17」はなぜ中途半端(?)なイメージがあるのか
「17」という数字は、1とそれ自身以外に約数を持たない「素数」である。
その前後の「16」や「18」という数字は、偶数であるとともに、「16」は2の四乗であり、「18」は2,3,6,9という約数を有することから、何となくとっつきやすいイメージがあり、比較的多くの場面で接する機会もあるものと思われる(そうかなと思われる人もいるかもしれないが)。
これに対して「17」と言われると、「えっ、何で」という印象を持たれてしまうのではないかと思われる。有名なピタゴラスやピタゴラス教団は、4×4(=16)の四辺形と3×6(=18)の四辺形の間に挟まれた位置にある「17」という数字を嫌っていたとの説もあるようだ。
以下では、数字の「17」が現れてくるいくつかの例を紹介したい。
その前後の「16」や「18」という数字は、偶数であるとともに、「16」は2の四乗であり、「18」は2,3,6,9という約数を有することから、何となくとっつきやすいイメージがあり、比較的多くの場面で接する機会もあるものと思われる(そうかなと思われる人もいるかもしれないが)。
これに対して「17」と言われると、「えっ、何で」という印象を持たれてしまうのではないかと思われる。有名なピタゴラスやピタゴラス教団は、4×4(=16)の四辺形と3×6(=18)の四辺形の間に挟まれた位置にある「17」という数字を嫌っていたとの説もあるようだ。
以下では、数字の「17」が現れてくるいくつかの例を紹介したい。
17頭のラクダの分配
数字の「17」が現れてくる有名な話があり、これは概ね以下のようなものである。
あるところで、ラクダ(馬でも羊でもよいが、アラブ世界の話に由来しているとのことで、ラクダとされることが多いようだ)を17頭所有していた人が亡くなった。その人には3人の男の子どもがいた。遺言によれば、そのラクダの分配について「長男に2分の1、次男に3分の1、三男に9分の1を分配せよ」となっていた。ところが、17は2でも3でも9でも割り切れない。兄弟が困り果てていると、一人の通りがかりの旅人が、「自分の1頭のラクダを貸してあげるから、これで18頭になる。18なら2でも3でも9でも割り切れるだろう。」ということになった。これにより、長男は9頭、次男は6頭、三男は2頭を配分されることになり、3人に配分されるラクダの総数は17頭になった。残りの1頭は旅人がそのまま持ち帰っていった。めでたしめでたし。
これはまさに、旅人の知恵に感心させられるエピソードであるとともに、ある意味で「17」という数字の特性を表しているものとなっている(因みに、上記の分配方法は遺言通りになっていないではないかと思われる方もいらっしゃるかもしれないが、そんな野暮(?)なことは言わないということになっている)。
なお、この話は大変有名になったので、ある人が似たようなケースで同じような知恵を披露しようとして失敗したという「落ち」も付いている。
それは、同じ17頭のラクダの分配で「長男に2分の1、次男に3分の1、三男に6分の1を分配せよ」となっていたケースである。この場合、1頭を加えた18頭の分配は、長男は9頭、次男は6頭、三男は3頭を配分されることになり、3人に配分されるラクダの総数は18頭になってしまう。知恵を披露するつもりで貸した(つもりの)1頭まで兄弟に配分される形になってしまい、知恵を貸したつもりの人はラクダを1頭損してしまうことになる。
あるところで、ラクダ(馬でも羊でもよいが、アラブ世界の話に由来しているとのことで、ラクダとされることが多いようだ)を17頭所有していた人が亡くなった。その人には3人の男の子どもがいた。遺言によれば、そのラクダの分配について「長男に2分の1、次男に3分の1、三男に9分の1を分配せよ」となっていた。ところが、17は2でも3でも9でも割り切れない。兄弟が困り果てていると、一人の通りがかりの旅人が、「自分の1頭のラクダを貸してあげるから、これで18頭になる。18なら2でも3でも9でも割り切れるだろう。」ということになった。これにより、長男は9頭、次男は6頭、三男は2頭を配分されることになり、3人に配分されるラクダの総数は17頭になった。残りの1頭は旅人がそのまま持ち帰っていった。めでたしめでたし。
これはまさに、旅人の知恵に感心させられるエピソードであるとともに、ある意味で「17」という数字の特性を表しているものとなっている(因みに、上記の分配方法は遺言通りになっていないではないかと思われる方もいらっしゃるかもしれないが、そんな野暮(?)なことは言わないということになっている)。
なお、この話は大変有名になったので、ある人が似たようなケースで同じような知恵を披露しようとして失敗したという「落ち」も付いている。
それは、同じ17頭のラクダの分配で「長男に2分の1、次男に3分の1、三男に6分の1を分配せよ」となっていたケースである。この場合、1頭を加えた18頭の分配は、長男は9頭、次男は6頭、三男は3頭を配分されることになり、3人に配分されるラクダの総数は18頭になってしまう。知恵を披露するつもりで貸した(つもりの)1頭まで兄弟に配分される形になってしまい、知恵を貸したつもりの人はラクダを1頭損してしまうことになる。
17年ゼミ(周期ゼミ、素数ゼミ)
17年ゼミというのは、「周期ゼミ」と呼ばれるものの1種で、「周期ゼミ」は一定の周期年数毎に大量に発生するセミのことを指している。17年ゼミと13年ゼミがあり、米国でのみ観測されるとされている。米国全体でみればどこかで大量発生しているのだが、1つの地方では決められた周期毎にしか大量発生しない形になっている。17も13も素数であることから「素数ゼミ」とも呼ばれている。
毎年、別の地方で大量発生するとすれば、17年ゼミは17個の、13年ゼミは13個の年次集団があることになるが、実際には絶滅した年次集団もあり、米国のどこでも周期ゼミが発生しない年もあるようだ。
それではなぜ「17年(あるいは13年)」なのかということになる。これについては、捕食者や寄生虫の周期と同期して発生する可能性を回避するためであると言われているようだ。素数であれば、他の周期を有するものと重なる機会は限定されることになる(例えば、17年ゼミの場合、3年周期の捕食者等とは51年毎、4年周期の捕食者等とは68年毎、5年周期の捕食者等とは85年毎にしか、同時に大量発生しない)。なお、素数ゼミ以外のセミの周期は一般的に4年から5年と言われており、これらのセミとの競合関係も回避できることになる。ある意味で、他のセミ等とは異なる周期で大量発生することで、個体の生存に有利な状況を作り出している形になっているようだ。
毎年、別の地方で大量発生するとすれば、17年ゼミは17個の、13年ゼミは13個の年次集団があることになるが、実際には絶滅した年次集団もあり、米国のどこでも周期ゼミが発生しない年もあるようだ。
それではなぜ「17年(あるいは13年)」なのかということになる。これについては、捕食者や寄生虫の周期と同期して発生する可能性を回避するためであると言われているようだ。素数であれば、他の周期を有するものと重なる機会は限定されることになる(例えば、17年ゼミの場合、3年周期の捕食者等とは51年毎、4年周期の捕食者等とは68年毎、5年周期の捕食者等とは85年毎にしか、同時に大量発生しない)。なお、素数ゼミ以外のセミの周期は一般的に4年から5年と言われており、これらのセミとの競合関係も回避できることになる。ある意味で、他のセミ等とは異なる周期で大量発生することで、個体の生存に有利な状況を作り出している形になっているようだ。
17歳
日本においても、2022年4月から18歳が成人年齢(又は成年年齢)となったが、多くの国では18歳が成人年齢となっている。その意味で17歳は成人になる丁度一歩手前ということになる。その意味では「17」という数字は、今一歩「未完成」や「未熟」といったイメージが持たれることになるのではないかと思われる。
映画や音楽作品等のタイトルに「17歳」という用語が使用されていることを眼にする機会もあると思われるが、こうした意味合いで使用されているのではないかと推測される。
映画や音楽作品等のタイトルに「17歳」という用語が使用されていることを眼にする機会もあると思われるが、こうした意味合いで使用されているのではないかと推測される。
正十七角形は定規とコンパスで描ける
以前の研究員の眼「数字の「7」に関わる各種の話題-「7」は何で人気が高い特別な数字として考えられているのか?-」(2020.6.1)で、「正七角形は定規とコンパスでは描けない」と述べた。
そうすると、殆どの人が、当然に正十七角形も定規とコンパスでは描けないのではないかと思われるだろう。ところが驚くことに、なんと「正十七角形は定規とコンパスで描ける」。
実は、正n角形が作図可能であるための必要十分条件は、
「n=2Np1p2・・・pk となる 0 以上の整数 N と互いに異なるフェルマー素数 p1,p2,・・・,pkが存在する。」
ということになっている。ここで、「フェルマー素数」というのは,0以上の整数kを用いて、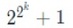 と表せる素数を言う。
と表せる素数を言う。
例えば、3(k=0)、5(k=1)、17(k=2)はフェルマー素数となる。これにより、正三角形や正方形(4=2×2)、正五角形、正六角形(6=2×3)は作図可能だが、正七角形は作図できない、一方で正十七角形は作図可能、ということになる。
この証明はかなり難しいので、興味のある方は専門書を参照していただきたい。先の研究員の眼で、「正七角形は定規とコンパスでは描けない」ことは、1796年にドイツの偉大な数学者カール・フリードリヒ・ガウス(Carl Friedrich Gauss)によって初めて証明された、と述べたが、同時に正十七角形が作図可能であることもガウスによって証明されている。
そうすると、殆どの人が、当然に正十七角形も定規とコンパスでは描けないのではないかと思われるだろう。ところが驚くことに、なんと「正十七角形は定規とコンパスで描ける」。
実は、正n角形が作図可能であるための必要十分条件は、
「n=2Np1p2・・・pk となる 0 以上の整数 N と互いに異なるフェルマー素数 p1,p2,・・・,pkが存在する。」
ということになっている。ここで、「フェルマー素数」というのは,0以上の整数kを用いて、
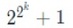 と表せる素数を言う。
と表せる素数を言う。例えば、3(k=0)、5(k=1)、17(k=2)はフェルマー素数となる。これにより、正三角形や正方形(4=2×2)、正五角形、正六角形(6=2×3)は作図可能だが、正七角形は作図できない、一方で正十七角形は作図可能、ということになる。
この証明はかなり難しいので、興味のある方は専門書を参照していただきたい。先の研究員の眼で、「正七角形は定規とコンパスでは描けない」ことは、1796年にドイツの偉大な数学者カール・フリードリヒ・ガウス(Carl Friedrich Gauss)によって初めて証明された、と述べたが、同時に正十七角形が作図可能であることもガウスによって証明されている。
17は最小のレイランド素数
「レイランド数」というのは、英国の数学者ポール・レイランド(Paul Leyland)によって発見されたもので、xy+yx (xとyは1より大きい整数)という形で表される数のことを言う。
例えば、8(=22+22)、17(=32+23)、32(=42+24)、54(=33+33)、57(=52+25)というような具合である。
これに対して、レイランド数でもあり素数でもあるものを「レイランド素数」と呼んでいる。レイランド数そのものは上でいくつかの例を挙げたように数多くあるが、レイランド素数はそれに比べると極めて限られている。
その中で「17」は、レイランド素数であり、しかも最小のものとなっている。
2番目のレイランド素数は「593=92+29」で、3番目のレイランド素数は「32,993=152+215」となっている。2012年12月時点で、86562929 + 29298656 (30008桁)が素数であることが証明され、現時点では証明された最大のレイランド素数と考えられているようだ。なお、3147389 + 9314738 などの巨大な素数候補も多くあるようだが、それ以上のことはわかっていない。
巨大なレイランド素数を研究することは、素数であるか否かを判定するコンピュータープログラムの改善につながるとされているようだ。
例えば、8(=22+22)、17(=32+23)、32(=42+24)、54(=33+33)、57(=52+25)というような具合である。
これに対して、レイランド数でもあり素数でもあるものを「レイランド素数」と呼んでいる。レイランド数そのものは上でいくつかの例を挙げたように数多くあるが、レイランド素数はそれに比べると極めて限られている。
その中で「17」は、レイランド素数であり、しかも最小のものとなっている。
2番目のレイランド素数は「593=92+29」で、3番目のレイランド素数は「32,993=152+215」となっている。2012年12月時点で、86562929 + 29298656 (30008桁)が素数であることが証明され、現時点では証明された最大のレイランド素数と考えられているようだ。なお、3147389 + 9314738 などの巨大な素数候補も多くあるようだが、それ以上のことはわかっていない。
巨大なレイランド素数を研究することは、素数であるか否かを判定するコンピュータープログラムの改善につながるとされているようだ。
イタリアでは17は忌み数
イタリア、特に南イタリアでは「17」という数字が「忌み数」とされているようだ。墓石に刻まれる「VIXI(ラテン語で『私は生きることを終えた』(=『私は死んでいる』)」という文字を入れ替えると、ローマ数字の「XVII(17)」になるということがその理由のようである。また、旧約聖書に記されたノアの大洪水も、ノアが600歳の時の第2の月の17日に起きたと言われている。
このため、イタリアでは「17」が付く部屋番号や階数が避けられ、またイタリアの航空会社には「17列」の客席が存在しないこともある、と言われているようだ。イタリアでは、「13日の金曜日」ならぬ「17日の金曜日」が特に不幸な日であると考えられている、とのことである。
なお、数字の「17」は、その他のギリシャとラテンを起源とする国でも不運であると考えられているようで、「17という数字に対する恐怖」をイタリア語でEptacaidecafobia(ギリシャ語のδεκαεπτάdekaepta(17)とφόβοςphóbos(恐怖)に由来、英語でHeptadecaphobia、日本語でヘプタデカフォビア)と呼んでいる。
このため、イタリアでは「17」が付く部屋番号や階数が避けられ、またイタリアの航空会社には「17列」の客席が存在しないこともある、と言われているようだ。イタリアでは、「13日の金曜日」ならぬ「17日の金曜日」が特に不幸な日であると考えられている、とのことである。
なお、数字の「17」は、その他のギリシャとラテンを起源とする国でも不運であると考えられているようで、「17という数字に対する恐怖」をイタリア語でEptacaidecafobia(ギリシャ語のδεκαεπτάdekaepta(17)とφόβοςphóbos(恐怖)に由来、英語でHeptadecaphobia、日本語でヘプタデカフォビア)と呼んでいる。
その他に数字の17が現れてくる例
年忌法要は、「一周忌」以後、三回忌、七回忌、十三回忌、十七回忌、二十三回忌、二十七回忌、三十三回忌等があり、「17」の数字が表れてくる。「十七回忌」は、没年の16年後に行われる法要である。これは、仏教において、「3」と「7」が特別視されていることによるもののようだ。
「3」については、何事も「有無」、「勝負」、「損得」といった形で物事を2分して考えるような世界において、2を超えて、悟りを目指す「中道」な生き方をする、ということを表しているようだ。
また、「7」については、やはり「六道」(全ての衆生が生前の業因によって生死を繰り返す六つの迷いの世界(即ち、地獄・餓鬼・畜生・阿修羅・人間・天上))の世界を超えて悟りに至る、という意味において、6を超える7という数字が大切にされているようだ。
従って、「17」そのものが特別視されているというわけではない。
「3」については、何事も「有無」、「勝負」、「損得」といった形で物事を2分して考えるような世界において、2を超えて、悟りを目指す「中道」な生き方をする、ということを表しているようだ。
また、「7」については、やはり「六道」(全ての衆生が生前の業因によって生死を繰り返す六つの迷いの世界(即ち、地獄・餓鬼・畜生・阿修羅・人間・天上))の世界を超えて悟りに至る、という意味において、6を超える7という数字が大切にされているようだ。
従って、「17」そのものが特別視されているというわけではない。
SDGsは17のゴールで構成されているが
2015年9月の国連サミットで加盟国の全会一致で採択された「持続可能な開発のための2030アジェンダ」に記載された,2030年までに持続可能でよりよい世界を目指す国際目標である、SDGs(Sustainable Development Goals:持続可能な開発目標)は、17のゴール、169のターゲットで構成されている。なぜ「17」なのかについては、恐らくたまたま17になっただけなのだと思われるが、もしかしたら、「17」に拘る何か特別な理由があるのかもしれないとも思ってしまう。もしご存じの方がいらっしゃれば、是非ご教示いただければと思っている。
最後に
今回は、数字の「17」に関わる各種の話題について、紹介してきた。
「17」という、一見すると中途半端なイメージを有する数字も、結構興味深い形で現れてくるな、と感じられたのではないかと思っている。
皆さんも、何気ない数字に関心を抱いて、知的探求を進めていただければと感じた次第である。
「17」という、一見すると中途半端なイメージを有する数字も、結構興味深い形で現れてくるな、と感じられたのではないかと思っている。
皆さんも、何気ない数字に関心を抱いて、知的探求を進めていただければと感じた次第である。
(2022年05月20日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/11/04 | 数字の「26」に関わる各種の話題-26という数字で思い浮かべる例は少ないと思われるが- | 中村 亮一 | 研究員の眼 |
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
新着記事
-
2025年11月07日
次回の利上げは一体いつか?~日銀金融政策を巡る材料点検 -
2025年11月07日
個人年金の改定についての技術的なアドバイス(欧州)-EIOPAから欧州委員会への回答 -
2025年11月07日
中国の貿易統計(25年10月)~輸出、輸入とも悪化。対米輸出は減少が続く -
2025年11月07日
英国金融政策(11月MPC公表)-2会合連続の据え置きで利下げペースは鈍化 -
2025年11月06日
世の中は人間よりも生成AIに寛大なのか?
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【数字の「17」は結構興味深い数字だって知っていますか】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
数字の「17」は結構興味深い数字だって知っていますかのレポート Topへ



















 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




