- シンクタンクならニッセイ基礎研究所 >
- 経済 >
- 財政・税制 >
- 「地方財源不足額」は本当に解消されているのか?―先送りされ続ける臨時財政対策債の償還財源確保
2018年07月13日
文字サイズ
- 小
- 中
- 大
付論――臨時財政対策債の理論償還費の推定方法
1|臨時財政対策債の元利金償還費
個別地方公共団体の地方交付税算定過程において、「基準財政需要額」に算入される臨時財政対策債の理論償還費は、他の費目と同様に、「単位費用×補正係数×測定単位」として求められた金額の積算値として算定される。その理論償還費は元金償還費と利払費を両方含むものであり、既往債の年度(発行可能額の割当年度)毎に「3年据置の定時償還方式」による「元金均等償還」が仮想されている10。具体的には、t年度における理論償還費Atは次の算式で表現することができる。
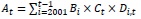 ・・・(1)
・・・(1)
ただしAt:t年度における理論償還費、Bi:2001年度以降のi年度既往債の発行可能額(千円単位、2001年度以降算定前年度までが集計対象)、Ct:t年度における単位費用(測定単位当たりの償還費)、Di,t:i年度に発行された既往債に対して適用されるt年度における補正係数
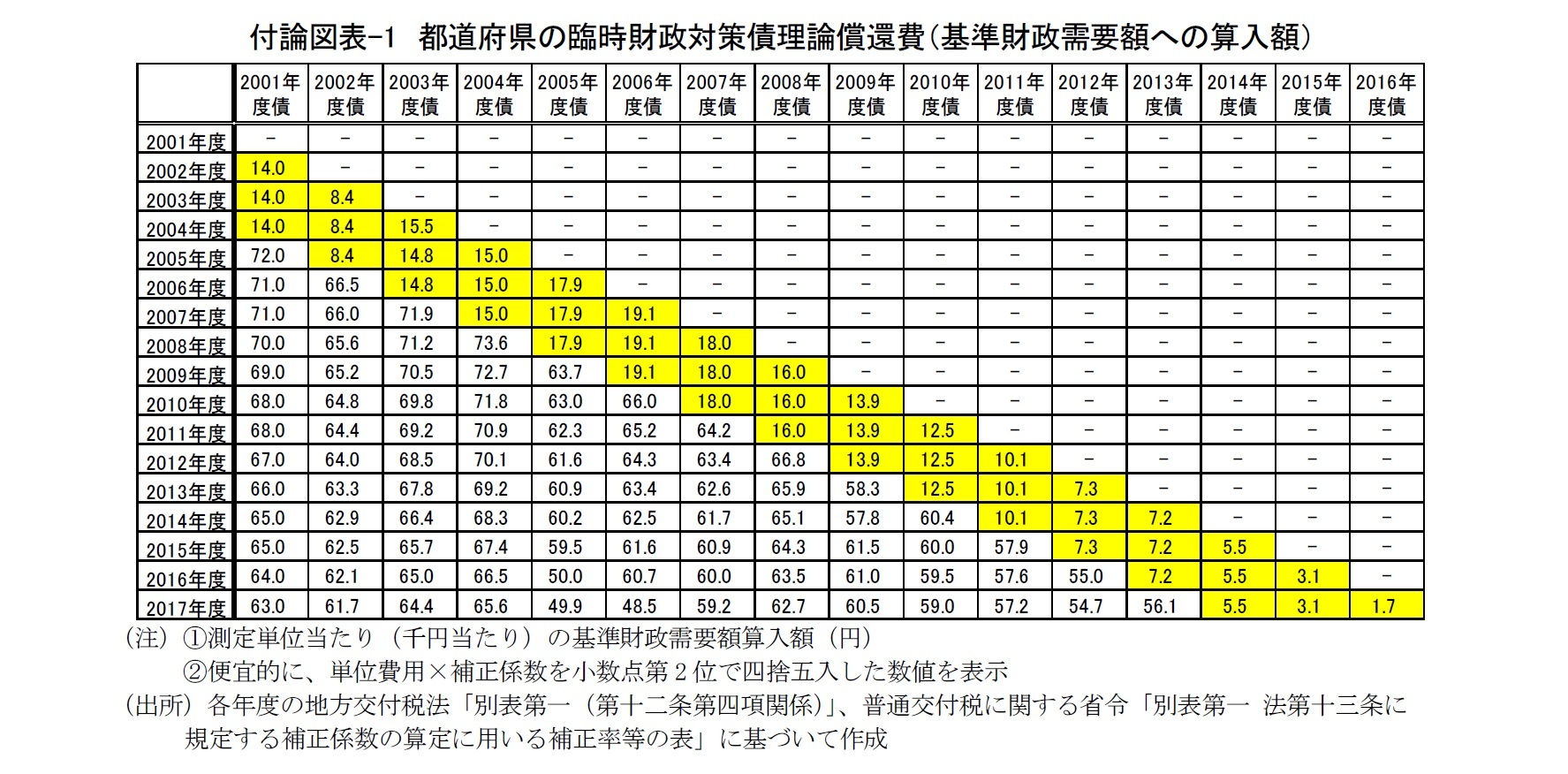
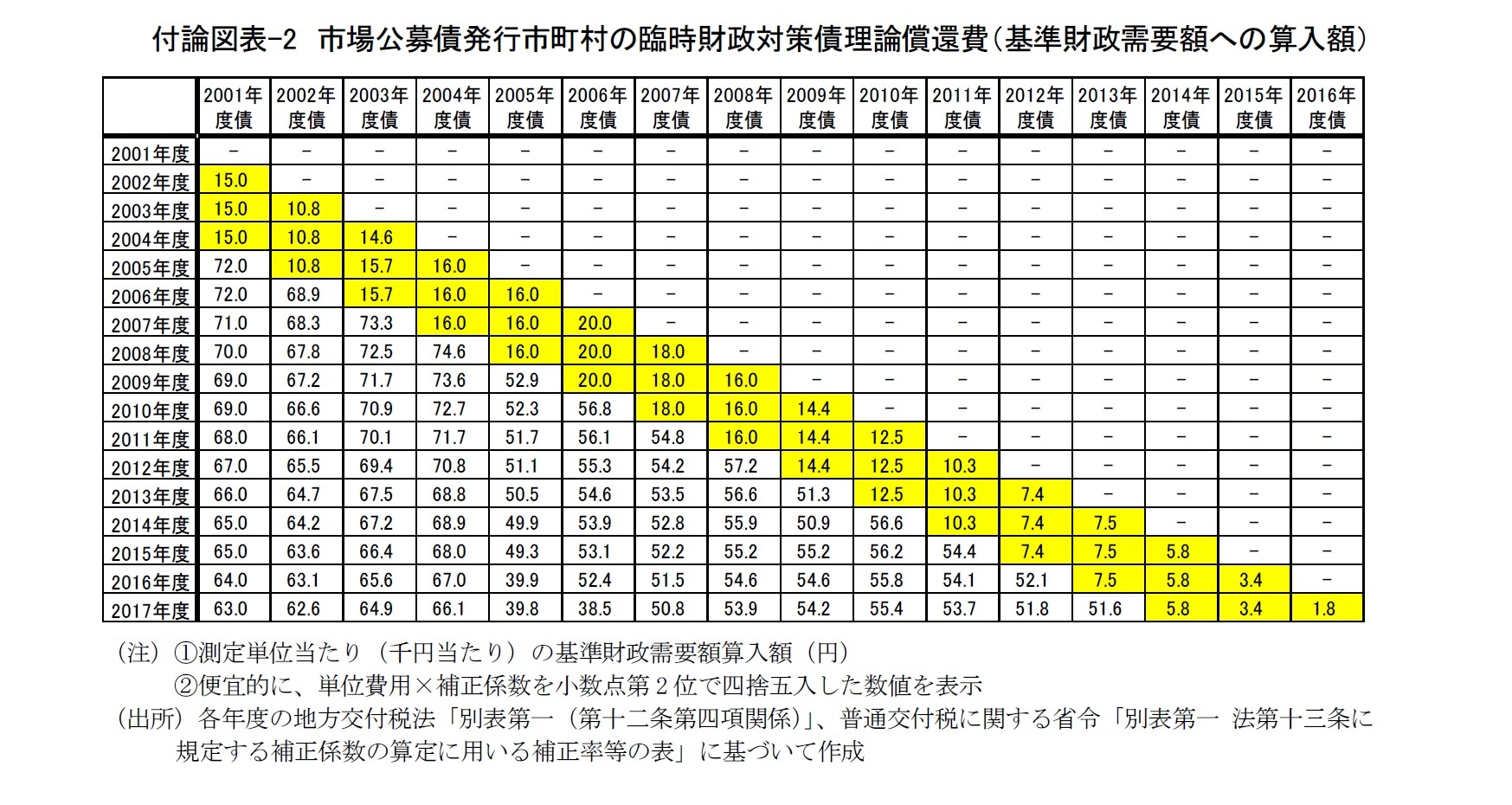
単位費用Ctに関しては、基準財政需要額算定の各年度において、都道府県と市町村のそれぞれに単一の数値が設定されている。各年度に発行された既往債に対して適用されるt年度の補正係数Di,tに関しては、都道府県については、基準財政需要額算定の各年度において単一の数値が設定されているが、市町村については、市場公募債発行市町村(政令市と東京特別区)とその他の市町村とで異なった数値が設定されている。これらを踏まえ、t年度におけるi年度債1000円当たりの理論償還費Ei,tを、Ei,t=Ct×Di,tとして定義すれば、都道府県、市場公募債発行市町村、他の市町村の2002年度以降2016年度までの各年度におけるEi,tは、以下の表のようにまとめることができる。
個別地方公共団体の地方交付税算定過程において、「基準財政需要額」に算入される臨時財政対策債の理論償還費は、他の費目と同様に、「単位費用×補正係数×測定単位」として求められた金額の積算値として算定される。その理論償還費は元金償還費と利払費を両方含むものであり、既往債の年度(発行可能額の割当年度)毎に「3年据置の定時償還方式」による「元金均等償還」が仮想されている10。具体的には、t年度における理論償還費Atは次の算式で表現することができる。
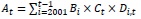 ・・・(1)
・・・(1)ただしAt:t年度における理論償還費、Bi:2001年度以降のi年度既往債の発行可能額(千円単位、2001年度以降算定前年度までが集計対象)、Ct:t年度における単位費用(測定単位当たりの償還費)、Di,t:i年度に発行された既往債に対して適用されるt年度における補正係数
単位費用Ctに関しては、基準財政需要額算定の各年度において、都道府県と市町村のそれぞれに単一の数値が設定されている。各年度に発行された既往債に対して適用されるt年度の補正係数Di,tに関しては、都道府県については、基準財政需要額算定の各年度において単一の数値が設定されているが、市町村については、市場公募債発行市町村(政令市と東京特別区)とその他の市町村とで異なった数値が設定されている。これらを踏まえ、t年度におけるi年度債1000円当たりの理論償還費Ei,tを、Ei,t=Ct×Di,tとして定義すれば、都道府県、市場公募債発行市町村、他の市町村の2002年度以降2016年度までの各年度におけるEi,tは、以下の表のようにまとめることができる。
これらを(1)式に当てはめて積算を行えば、都道府県についても、市町村(同一都道府県内集計値)についても、総務省「地方交付税等関係計数資料」に掲載されている臨時財政対策債の理論償還費をほぼ誤差なく再現することができる。
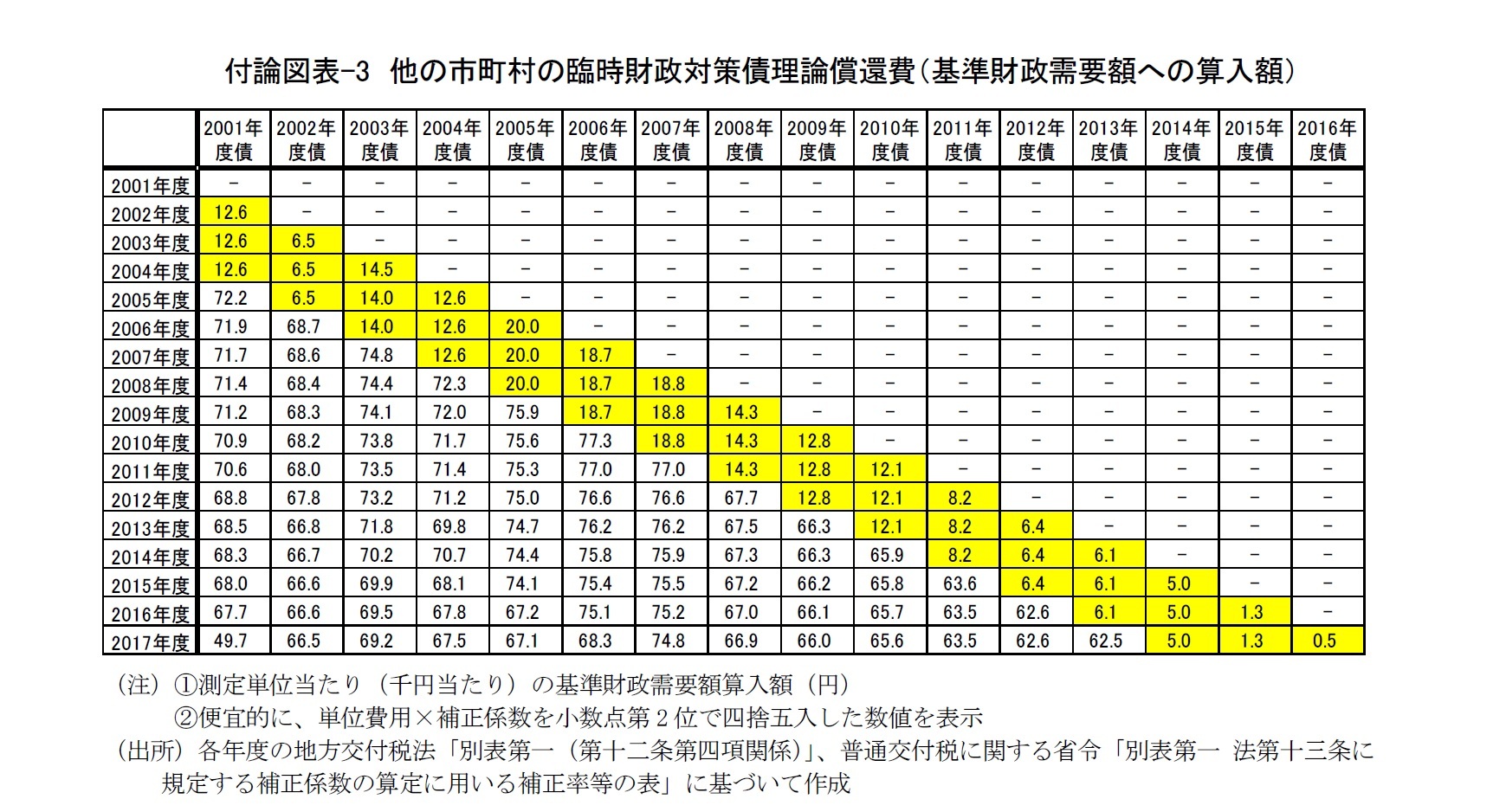
10 仮想される償還年数が複数の場合は、それぞれの理論償還費の加重平均値として算定される。例えば、後掲の付論図表-3において、2001年度債の16年度目(2017年度)の理論償還費が前年度から急減しているのは、仮想された15年債と20年債のうち、15年債部分の理論償還が完了したことによるものと推察される。
10 仮想される償還年数が複数の場合は、それぞれの理論償還費の加重平均値として算定される。例えば、後掲の付論図表-3において、2001年度債の16年度目(2017年度)の理論償還費が前年度から急減しているのは、仮想された15年債と20年債のうち、15年債部分の理論償還が完了したことによるものと推察される。
2|臨時財政対策債の元金償還費
t年度におけるi年度債の理論償還費Ei,tは、本来は元金償還費Fi,tと利払費Gi,tの合計額として決定されているはずであるが(後の(2)式)、元金償還費と利払費の理論値は公表されておらず、算定方法も開示されていない。そこで、以下の考え方に基づいて、推定されたEi,tを未知のFi,tとGi,tに分解する。
まず、発行年度にかかわらず、「据置期間3年の元金均等返済」が想定されているから、起債翌年度から3年度後までの3年間の元金償還額はゼロである((5)式)。若干の例外を除けば、その利払費の金額は同一である((6)式)。また、i年度債の表面金利riは、起債翌年度の償還費を1000円で除した値となる((3)式)。すなわち、以下の関係式が成り立つ。
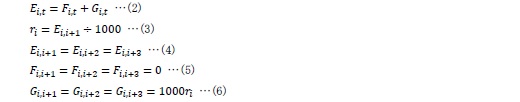
ただし、Ei,t:t年度におけるi年度債の理論償還費(1000円当たり)、Fi,t:t年度におけるi年度債の理論元金償還費、Gi,t:t年度における理論利払費、ri:i年度債の表面金利
t年度におけるi年度債の理論償還費Ei,tは、本来は元金償還費Fi,tと利払費Gi,tの合計額として決定されているはずであるが(後の(2)式)、元金償還費と利払費の理論値は公表されておらず、算定方法も開示されていない。そこで、以下の考え方に基づいて、推定されたEi,tを未知のFi,tとGi,tに分解する。
まず、発行年度にかかわらず、「据置期間3年の元金均等返済」が想定されているから、起債翌年度から3年度後までの3年間の元金償還額はゼロである((5)式)。若干の例外を除けば、その利払費の金額は同一である((6)式)。また、i年度債の表面金利riは、起債翌年度の償還費を1000円で除した値となる((3)式)。すなわち、以下の関係式が成り立つ。
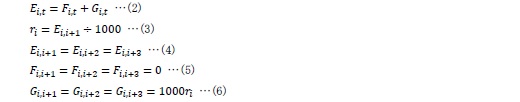
ただし、Ei,t:t年度におけるi年度債の理論償還費(1000円当たり)、Fi,t:t年度におけるi年度債の理論元金償還費、Gi,t:t年度における理論利払費、ri:i年度債の表面金利
また、起債後4年度目の利払費Gi,i+4は満額の元本残存に対応した額であるため、結果的には、3年度目までと同額である((7)式)。そのため、4年度目の元金償還費Fi,i+4は理論償還費Ei,i+4からこの利払費Gi,i+4を控除することによって、容易に求めることができる((8)式)。


さらに、起債後5年度目以降に関しては、前年度末の元本残存額Hi,t-1に金利riを乗じた額が利払費となる一方((10)式)、当年度末の元本残存額Hi,tは前年度末の元本残存額Hi,t-1から当年度の元金償還費Fi,tを控除した額となる((9)式)。これらの関係から、当年度の利払費の前年度からの変化額⊿Gi,tが負の値をとり、それが前年度の元金償還費Fi,t-1と金利riの積に等しいことが分かる((11)式)。すなわち、当年度の利払費Gi,tは前年度の利払費Gi,t-1から前年度の元金償還費Fi,t-1と金利riの積を控除した額に等しい((12)式)。また、元金償還費Fi,tは理論償還費Ei,tと利払費Gi,tの差として求められる((2)式)。
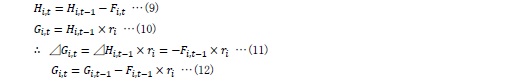
ただし、Hi,t:t年度末におけるi年度債の元本残存額
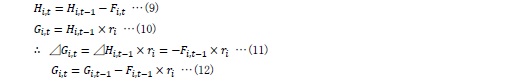
ただし、Hi,t:t年度末におけるi年度債の元本残存額
同様にして、6年度目以降の利払費変化額と元金償還費も逐次的に求めること可能であり、全年度の元金償還費を算出することができる。このようにして求めた各年度の元金償還費推定値は、厳密には、同一額にならないが、その理由は、端数等の年度間調整を施しているためと考えられる。
(お願い)本誌記載のデータは各種の情報源から入手・加工したものであり、その正確性と安全性を保証するものではありません。また、本誌は情報提供が目的であり、記載の意見や予測は、いかなる契約の締結や解約を勧誘するものではありません。
(2018年07月13日「基礎研レポート」)
石川 達哉
石川 達哉のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2018/12/28 | 同床異夢の臨時財政対策債-償還費を本当に負担するのは国か、地方か? | 石川 達哉 | 研究員の眼 |
| 2018/07/13 | 「地方財源不足額」は本当に解消されているのか?―先送りされ続ける臨時財政対策債の償還財源確保 | 石川 達哉 | 基礎研レポート |
| 2017/08/31 | 再び問われる交付税特会の行方-地方財政の健全性は高まったのか? | 石川 達哉 | 基礎研レポート |
| 2017/07/03 | 増大する地方公共団体の基金残高 その2-実は拡大している積立不足!? | 石川 達哉 | 研究員の眼 |
新着記事
-
2025年10月17日
EUの金融システムのリスクと脆弱性(2025秋)-欧州の3つの金融監督当局の合同委員会報告書 -
2025年10月17日
日本における「老衰死」増加の背景 -
2025年10月17日
選択と責任──消費社会の二重構造(1)-欲望について考える(2) -
2025年10月17日
首都圏の中古マンション価格~隣接する行政区単位での価格差は?~ -
2025年10月17日
「SDGs疲れ」のその先へ-2015年9月国連採択から10年、2030年に向け問われる「実装力」
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【「地方財源不足額」は本当に解消されているのか?―先送りされ続ける臨時財政対策債の償還財源確保】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
「地方財源不足額」は本当に解消されているのか?―先送りされ続ける臨時財政対策債の償還財源確保のレポート Topへ



















 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




