- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 誕生日が一致する確率-多くの人が集まる場では、誕生日の話題で盛り上がりませんか-
コラム
2016年12月19日

文字サイズ
- 小
- 中
- 大
問題(その2)
次に、特定の個人に関しての発生確率を考える。
問題 8 自分と同じ誕生日の人がいない確率 S0
問題 9 自分と誰かの誕生日が一致している確率
(自分と同じ誕生日の人が他に1人以上いる確率)T1(=1-S0)
問題10 自分と同じ誕生日の人が他に丁度1人いる確率 S1
問題11 自分と同じ誕生日の人が他に2人以上いる確率 T2
問題12 自分と同じ誕生日の人が他に丁度2人いる確率 S2
問題13 自分と同じ誕生日の人が他に3人以上いる確率 T3
問題14 自分と同じ誕生日の人が他に丁度3人いる確率 S3
以下、同様に、自分と同じ誕生日の人が丁度k人いる確率Skや自分と同じ誕生日の人が最低k人いる確率Tkが考えられる。この場合、
となる。
問題 8 自分と同じ誕生日の人がいない確率 S0
問題 9 自分と誰かの誕生日が一致している確率
(自分と同じ誕生日の人が他に1人以上いる確率)T1(=1-S0)
問題10 自分と同じ誕生日の人が他に丁度1人いる確率 S1
問題11 自分と同じ誕生日の人が他に2人以上いる確率 T2
問題12 自分と同じ誕生日の人が他に丁度2人いる確率 S2
問題13 自分と同じ誕生日の人が他に3人以上いる確率 T3
問題14 自分と同じ誕生日の人が他に丁度3人いる確率 S3
以下、同様に、自分と同じ誕生日の人が丁度k人いる確率Skや自分と同じ誕生日の人が最低k人いる確率Tkが考えられる。この場合、
Tk=S1+S2+ ・・・・・ + Sk、あるいは、Sk = Tk-T(k-1)
となる。
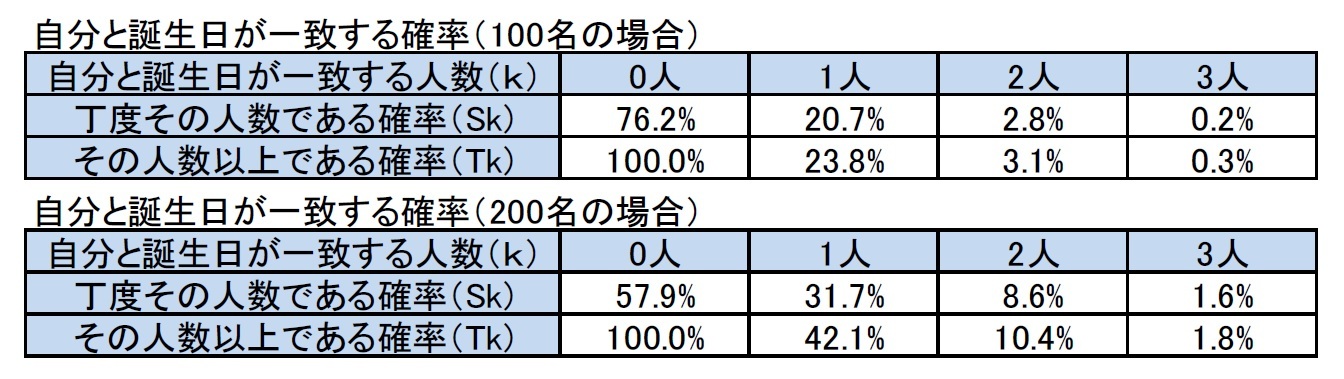
問題(その2)の解答
まとめ
以前の研究員の眼と同様に、今回の結果についても驚かれた方が多いのではないかと思われる。
ここでは誕生日をテーマにしているが、一般的に人間は、何かの事象の発生確率を想定する場合に、無意識的に自分を中心に起こるケースを想定して、その発生確率は低いものだと想定しているのではないか。ところが、グループ全体として考える場合には、個人が想定しているよりもかなり高い確率でその事象が発生することになる。
このことは、物事を考えていく場合に何か示唆するものがあるのではないかと思われる。
順列・組み合わせの問題については、中学・高校時代にかなり苦労された方も多いのではないかと思う。しかし、こうやって考えてみると、その解答を導き出すのは必ずしも易しくないとしても、その結果には感動させられることもあるのではないかと思われる。これを機に、今一度若い頃に戻って、いろいろな順列・組み合わせが関係してくる確率の問題を考えてみるのも、頭の体操になってよいのではないか。
ここでは誕生日をテーマにしているが、一般的に人間は、何かの事象の発生確率を想定する場合に、無意識的に自分を中心に起こるケースを想定して、その発生確率は低いものだと想定しているのではないか。ところが、グループ全体として考える場合には、個人が想定しているよりもかなり高い確率でその事象が発生することになる。
このことは、物事を考えていく場合に何か示唆するものがあるのではないかと思われる。
順列・組み合わせの問題については、中学・高校時代にかなり苦労された方も多いのではないかと思う。しかし、こうやって考えてみると、その解答を導き出すのは必ずしも易しくないとしても、その結果には感動させられることもあるのではないかと思われる。これを機に、今一度若い頃に戻って、いろいろな順列・組み合わせが関係してくる確率の問題を考えてみるのも、頭の体操になってよいのではないか。
(2016年12月19日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/09/02 | 欧州大手保険グループの2025年上期末SCR比率等の状況-ソルベンシーII等に基づく数値結果報告と資本管理等に関係するトピック- | 中村 亮一 | 基礎研レポート |
| 2025/08/20 | 曲線にはどんな種類があって、どう社会に役立っているのか(その12)-螺旋と渦巻の応用- | 中村 亮一 | 研究員の眼 |
| 2025/08/07 | 複素数について(その3)-複素数の工学・物理学への応用- | 中村 亮一 | 研究員の眼 |
| 2025/08/04 | EIOPAがソルベンシーIIのレビューに関する最初のRTS(案)等のセットを欧州委員会に提出等 | 中村 亮一 | 保険・年金フォーカス |
新着記事
-
2025年09月03日
ブラジルGDP(2025年4-6月期)-内需は弱く、輸出も減速 -
2025年09月03日
増え行く単身世帯と消費市場への影響(4)-教養娯楽・交際費から見る「自分時間」「人間関係」「自己表現」への投資 -
2025年09月03日
DC制度運営の再点検を -
2025年09月03日
成立した年金制度改正が将来の年金額に与える影響 -
2025年09月03日
日本の人的資本投資の現状と課題
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【誕生日が一致する確率-多くの人が集まる場では、誕生日の話題で盛り上がりませんか-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
誕生日が一致する確率-多くの人が集まる場では、誕生日の話題で盛り上がりませんか-のレポート Topへ


















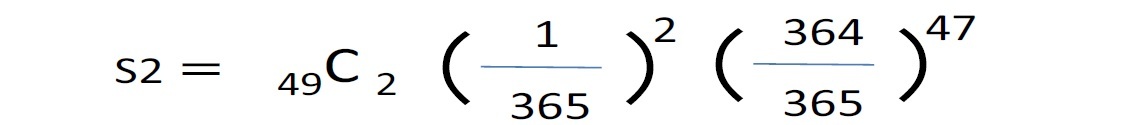


 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




